Kruskal重构树
一、最小生成树 & Kruskal
最小生成树:将无向连通图的一些边删掉,使得剩下的点和边构成一棵树,且这棵树的边权总和最小,这样的树称为最小生成树。
Kruskal:每次选不属于同一生成树的且权值最小的边的顶点,将边加入生成树,并将所在的2个生成树合并,直到只剩一个生成树。复杂度 O( m log m )。

#include <bits/stdc++.h> using namespace std; struct node {int a,b,Len;}A[100005]; bool cmp(node x,node y) {return x.Len<y.Len;} int n,m,Father[100005],x,y,k,Cnt,ans; int getFather(int x) { if(x==Father[x]) return Father[x]; else {Father[x]=getFather(Father[x]);return Father[x];} } int main() { scanf("%d%d",&n,&m); for(register int i=1;i<=m;++i) scanf("%d%d%d",&A[i].a,&A[i].b,&A[i].Len); for(register int i=1;i<=n;++i) Father[i]=i; sort(A+1,A+m+1,cmp); while(Cnt<n-1) { ++k,x=getFather(A[k].a),y=getFather(A[k].b); if(x!=y) Father[y]=x,ans+=A[k].Len,++Cnt; } printf("%d",ans); }
二、Kruskal 重构树
1. 过程: 按照kruskal规则连边,对于要连接的边( a , b ),边权为c,令 x = getFather ( a ) , y = getFather ( b ) 。 若 x != y , 新建一个节点 z 作为 x 和 y 的父亲,z 的点权为边 ( a , b ) 的边权,即 father [ x ] = z , father [ y ] = z , Val [ z ] = c ;
2. 性质:
(1). 重构树是节点总数为 2n-1 的 二叉树 ;
(2). 重构树是一个根堆(最小生成树 -- 大根堆,最大生成树 -- 小根堆);
(3). 重构树 ( 按最小生成树重构 ) 中任意两点 a , b 的路径中的最大边权为它们LCA ( a , b ) 的点权。也是原图中,a , b 路径中最大边 权的最小值 ;
重构树 ( 按最大生成树重构 ) 中任意两点 a , b 的路径中的最 小边权为它们LCA ( a , b ) 的点权。也是原图中,a , b 路径中最小边权的最大值 ;
(4). 如果原图不连通,会得到重构树森林;
(5). 只有叶子节点是原图中的点,其他非叶节点代表的是原图中的边。
3. 实现(见例题一)。
三、例题
(一)、NKOJ-2495【NOIP2013-D1T3】货车运输
问题描述:
A国有n座城市,编号从1到n,城市之间有m条双向道路。
每一条道路对车辆都有重量限制,简称限重。
现在有q辆货车在运输货物,司机们想知道每辆车在不超过车辆限重的情况下,最多能运多重的货物。
输入格式:
第一行有两个用一个空格隔开的整数 n,m,表示 A 国有n座城市和m条道路。
接下来m行,每行3个整数x,y,z,表示从x号城市到y号城市有一条限重为z的道路(x≠y,两座城市之间可能有多条道路)
接下来一行有一个整数 q,表示有 q 辆货车需要运货。
接下来q行,每行两个整数x,y,之间用一个空格隔开,表示一辆货车需要从x城市运输货物到y城市(x≠y)。
输出格式:
输出共有 q 行,每行一个整数,表示对于这一辆货车,它的最大载重是多少。 如果货车不能到达目的地,输出-1。
数据范围:
对于 30%的数据,1<=n<=1000,1<=m<=10000,1<=q<=1000; 对于 60%的数据,1<=n<=1000,1<=m<=50000,1<=q<=1000; 对于 100%的数据,1<=n<=100000,1<=m<=500000,1<=q<=30000,0<=z<=100000。
这个就是个板题,按最大生成树建重构树,LCA ( x , y ) 的权值即为 x 到 y 路径上最大载重的最小值。
Code:

#pragma GCC optimize(2) #pragma GCC optimize(3) #include<bits/stdc++.h> using namespace std; bool Mark[200005]; int n,m,q,Fa[100005],K,tot(1),Father[100005][25],Deep[100005],pos,V[200005],Cnt,Head[200005],Next[200005],To[200005]; struct node {int x,y,z;}E[500005]; bool cmp(node x,node y) {return x.z>y.z;} #define gc (p1==p2&&(p2=(p1=buf)+fread(buf,1,65536,stdin),p1==p2)?EOF:*p1++) char buf[65536],*p1,*p2; inline int read() { char ch;int x(0); while((ch=gc)<48); do x=x*10+ch-48;while((ch=gc)>=48); return x; } inline int GetFa(int x) { if(Fa[x]==x) return x; return Fa[x]=GetFa(Fa[x]); } inline void ADD(int x,int y) {Next[++Cnt]=Head[x],Head[x]=Cnt,To[Cnt]=y;} inline void DFS(int x,int fa) { Mark[x]=1,Deep[x]=Deep[fa]+1,Father[x][0]=fa; for(register int i=0;Father[x][i];++i) Father[x][i+1]=Father[Father[x][i]][i]; for(register int i=Head[x];i;i=Next[i]) DFS(To[i],x); } inline int LCA(int u,int v) { if(Deep[u]>Deep[v]) swap(u,v); for(register int i=20;i>=0;--i) if (Deep[u]<=Deep[v]-(1<<i)) v=Father[v][i]; if(u==v) return u; for(register int i=20;i>=0;--i) if(Father[u][i]!=Father[v][i]) u=Father[u][i],v=Father[v][i]; return Father[u][0]; } int main() { n=pos=read(),m=read(),V[0]=-1; for(register int i=1;i<=2*n;++i) Fa[i]=i; for(register int i=1;i<=m;++i) E[i].x=read(),E[i].y=read(),E[i].z=read(); sort(E+1,E+m+1,cmp); while(tot<n&&K<m) { int x,y;x=GetFa(E[++K].x),y=GetFa(E[K].y); if(x!=y) V[++pos]=E[K].z,Fa[x]=pos,Fa[y]=pos,ADD(pos,x),ADD(pos,y),++tot; } for(register int i=pos;i;--i) if(!Mark[i]) DFS(i,0); q=read(); for(register int i=1,x,y;i<=q;++i) x=read(),y=read(),printf("%d\n",V[LCA(x,y)]); return 0; }
(二)、NKOJ-8437 删边
问题描述:
一个n个节点 m 条带权边的无向连通图。
有 q 次询问,每次询问图中 ki 个互不相同的点,你可以选择一个数 x,然后将图中所有边权小于等于 x 的边删除。求当删除这些边后 ki 个点互不连通时,求 x 的最小值。
注意,本题强制在线
输入格式:
第一行三个整数 n,m,q,表示无向连通图有 n 个节点,m 条边,q 次询问。 接下来 m 行,每行三个整数 u,v,w,表示 u,v 之间有一条边权为 w 的无向边。 接下来 q 行,每行第一个整数为 ki,表示第 i 次询问有 ki 个点。 之后有 ki 个整数 a′1,a′2,...,a′ki,真实询问的点 aj 为 aj′ 按位异或上 lastans 后的值。 lastans 为上一次询问的答案,初始时 lastans=0 。
输出格式:
共 q 行,每行一个整数表示每次询问的答案。
数据范围:
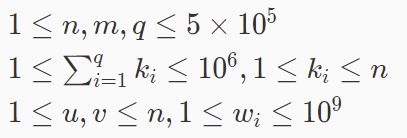
首先,要删除小于等于 x 的边,并且 x 要尽量小,所以按最大生成树重建。
但答案是什么呢?
对于 a , b 两点,答案显然是 LCA( a , b ) ,但k个数呢,是 k 个数的 LCA吗???
显然不是(反例很好构造),答案应该是K个数两两LCA权值的最大值,这样会计算k2次,q次询问,喜提TLE。
在重构树上,相邻两点的Lca的点权就是这两点直接所连的边的边权。因为是按照最大生成树建立的重构树,本质是小根堆。”距离”越远的两点,其Lca的深度可能越小,对应的点权也越小。那怎么确定两点的相邻关系的远近?
D F S 序!DFS序越接近的点,在树中越相邻。
所以:
(1)求出重构树的DFS序;
(2)对于第i次询问的ki个点,将它们放入容器A(A是vector),然后按DFS序排序。
(3)询问的答案 Ans [ i ] = max { V [ Lca (A1 ,A2 ) ], V [ Lca (A2, A3) ] , … , V [ Lca (Ak-1, Ak) ] } V [ x ] 为重构树中,x号点的点权 , A1,A2,…,Ak 为按DFS序排序后的 k 个点。
时间复杂度 O( log n * ∑ k )
Code:

#pragma GCC optimize(2) #pragma GCC optimize(3) #include<bits/stdc++.h> using namespace std; bool Mark[2000005]; int n,m,q,Fa[2000005],TOT,Left[2000005],K,tot(1),Father[2000005][25],Deep[2000005],pos,V[2000005],Cnt,Head[2000005],Next[2000005],To[2000005],Q[2000005]; struct node {int x,y,z;}E[2000005]; bool cmp1(node x,node y) {return x.z>y.z;} bool cmp2(int x,int y) {return Left[x]<Left[y];} #define gc (p1==p2&&(p2=(p1=buf)+fread(buf,1,65536,stdin),p1==p2)?EOF:*p1++) char buf[65536],*p1,*p2; inline int read() { char ch;int x(0); while((ch=gc)<48); do x=x*10+ch-48;while((ch=gc)>=48); return x; } inline int GetFa(int x) {if(Fa[x]==x) return x;return Fa[x]=GetFa(Fa[x]);} inline void ADD(int x,int y) {Next[++Cnt]=Head[x],Head[x]=Cnt,To[Cnt]=y;} inline void DFS(int x,int fa) { bool S(0); Mark[x]=1,Deep[x]=Deep[fa]+1,Father[x][0]=fa; for(register int i=0;Father[x][i];++i) Father[x][i+1]=Father[Father[x][i]][i]; for(register int i=Head[x];i;i=Next[i]) DFS(To[i],x),S=1; if(!S) Left[x]=++TOT; } inline int LCA(int u,int v) { if(Deep[u]>Deep[v]) swap(u,v); for(register int i=20;i>=0;--i) if (Deep[u]<=Deep[v]-(1<<i)) v=Father[v][i]; if(u==v) return u; for(register int i=20;i>=0;--i) if(Father[u][i]!=Father[v][i]) u=Father[u][i],v=Father[v][i]; return Father[u][0]; } int main() { n=pos=read(),m=read(),q=read(); for(register int i=1;i<=2*n;++i) Fa[i]=i; for(register int i=1;i<=m;++i) E[i].x=read(),E[i].y=read(),E[i].z=read(); sort(E+1,E+m+1,cmp1); while(tot<n&&K<m) { int x,y;x=GetFa(E[++K].x),y=GetFa(E[K].y); if(x!=y) V[++pos]=E[K].z,Fa[x]=pos,Fa[y]=pos,ADD(pos,x),ADD(pos,y),++tot; } for(register int i=pos;i;--i) if(!Mark[i]) DFS(i,0); for(register int i=1,k,Ans(0);i<=q;++i) { k=read(); for(register int j=1;j<=k;++j) Q[j]=read()^Ans; sort(Q+1,Q+k+1,cmp2),Ans=0; for(register int j=1;j<k;++j) Ans=max(Ans,V[LCA(Q[j],Q[j+1])]); printf("%d\n",Ans); } return 0; }
(三)、NKOJ-8438 路径权值
问题描述:
给定一个带边权的树,树上任意两点间的路径权值d(x,y)定义为x,y这两个点之间路径上的最小值, 树上任意一点x的权值Val(x)定义为这个点到树上其他所有点的路径权值和,即Val(x)=∑d(x,i), 1<=i<=n。 现求树上一点,使得这个点的权值最大,输出这个值。
输入格式:
第一行,一个整数 n(1≤n≤100000) ,树的点的个数,节点编号1到n。 接下来n−1行,每行三个整数 x,y,s(1≤x,y≤n,1≤s≤10000),表示编号为x的节点和编号为y的节点之间存在一条权值为s的边。
输出格式:
一行,树上的点的最大权值
按最大生成树重建,对路径 (a,b), LCA( a , b ) 即为路径上最小值。
问题是,怎么快速算出答案呢?
既然我们无法一条路径一条路径算贡献,那我们可以算每个点的贡献:
上面在Kruskal重构树的性质中有这么一条:重构树是一颗二叉树 ;
以 x 为根的子树中:对左儿子中一点,x 的贡献为 V [ x ] * Size [ Rs [ x ] ] ;对右儿子中一点,x 的贡献为 V [ x ] * Size [ Ls [ x ] ] (其中,V [ ] 为点权,Size [ ] 为子树大小,Ls [ ] 为左儿子,Rs [ ] 为右儿子);
一个儿子中所以点都要加上另一个儿子使 x 产生的贡献,很容易想到了 DFS序 + 树状数组,即:
Modify(In[Lt[i]], V[i]*Size[Rt[i]]) Modify(Out[Lt[i]]+1, -V[i]*Size[Rt[i]]) Modify(In[Rt[i]], V[i]*Size[Lt[i]]) Modify(Out[Rt[i]]+1, -V[i]*Size[Lt[i]])
最后答案是什么呢?
显然,Ans [ i ] = GetSum ( In [ i ] ) (GetSum为树状数组求和)。
Code:

#pragma GCC optimize(2) #pragma GCC optimize(3) #include<bits/stdc++.h> using namespace std; int n,K,Fa[200005],C[200005],Size[200005],tot,In[200005],Out[200005],pos,V[200005],Ls[200005],Rs[200005],Ans; struct node {int x,y,z;}E[100005]; bool cmp(node x,node y) {return x.z>y.z;} #define gc (p1==p2&&(p2=(p1=buf)+fread(buf,1,65536,stdin),p1==p2)?EOF:*p1++) char buf[65536],*p1,*p2; inline int read() { char ch;int x(0); while((ch=gc)<48); do x=x*10+ch-48;while((ch=gc)>=48); return x; } inline int GetFa(int x) {if(Fa[x]==x) return x;return Fa[x]=GetFa(Fa[x]);} inline void Modify(int x,int y) {while (x<=pos) C[x]+=y,x+=(x&(-x));} inline int GetSum(int x) {int RET=0;while(x) RET+=C[x],x-=(x&(-x));return RET;} inline void DFS(int x) { In[x]=++tot; if(Ls[x]) DFS(Ls[x]),Size[x]+=Size[Ls[x]],DFS(Rs[x]),Size[x]+=Size[Rs[x]]; Out[x]=tot; if(!Ls[x]) {Size[x]=1;return;} Modify(In[Ls[x]],V[x]*Size[Rs[x]]),Modify(Out[Ls[x]]+1,-V[x]*Size[Rs[x]]),Modify(In[Rs[x]],V[x]*Size[Ls[x]]),Modify(Out[Rs[x]]+1,-V[x]*Size[Ls[x]]); } int main() { n=pos=read(); for(register int i=1;i<=2*n;++i) Fa[i]=i; for(register int i=1;i<n;++i) E[i].x=read(),E[i].y=read(),E[i].z=read(); sort(E+1,E+n,cmp); while(K<n-1) { int x,y; x=GetFa(E[++K].x),y=GetFa(E[K].y),V[++pos]=E[K].z,Fa[x]=pos,Fa[y]=pos,Ls[pos]=x,Rs[pos]=y; } DFS(pos); for(register int i=1;i<=n;++i) Ans=max(Ans,GetSum(In[i])); printf("%d",Ans); return 0; }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号