树链剖分

嗟乎！树剖之难者线段树也，非树剖也。

（文末有*****）

　　树链顾名思义，是树上的路径。树链剖分，就是将一棵树分成若干链，再用数据结构（如线段树）去维护每一条链，明显复杂度 O(log n) 。

　　树链剖分，又名“重链剖分”，那什么是重链呢？

　　我们将树中的边分为轻边和重边，定义Size(x) 为以 x 为根的子树的节点个数，令 x 的儿子中 y 的Size()最大，那么，我们称边(x,y)为重边，y为x的重儿子。而由重边构成的链即为重链。

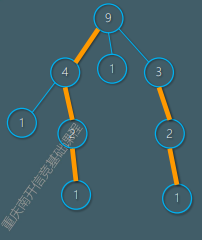
（如图，其中粗边为重边，9-4-2-1是一条重链）（图片来自老板的PPT）

　　性质：从根到某一点的路径上，轻边不超过O(logN)条，重链也不超过 O(logN)条。

实现：

　进行两次DFS：

　　1. 找出重儿子（代码中的DFS1）

　　2. 找出重链（代码中的DFS2）：以根节点为起点，沿重边向下拓展，拉成重链。不在当前重链上的节点，都以该节点为起点向下重新拉一条重链。同时，对每个重新编号（记在 Id[ ] 中），这样，每条重链就相当于一段编号连续的区间，便于用数据结构维护。

inline void DFS1(int x,int fa,int deep)
{
    int Max(0);
    Size[x]=1,Fa[x]=fa,Deep[x]=deep;
    for(register int i=Head[x],j;i;i=Next[i])
    {
        j=To[i];
        if(j==fa) continue;
        DFS1(j,x,deep+1),Size[x]+=Size[j];
        if(Size[j]>Max) Max=Size[j],Son[x]=j;
    }
}

inline void DFS2(int x,int anc)
{
    Top[x]=anc,Id[x]=++Cnt,Trans[Cnt]=x;
    if(Son[x]) DFS2(Son[x],anc);
    for(register int i=Head[x],j;i;i=Next[i])
    {
        j=To[i];
        if(j==Fa[x]||j==Son[x]) continue;
        DFS2(j,j);
    }
}

DFS

修改&查询：

　　两种操作的本质差不多，所以放在一起说，可以分为两种情况：

　　　　情况a：U，V 在同一条重链上，直接对 Id[U] 到 Id[V] 这段区间操作。

　　　　情况b：U，V 不在同一条重链上，一边进行修改，一边将U和V往同一条重链上靠，然后就变成了“情况a”。但是，怎么靠呢？？？

　　　　方法：每次在U和V中，选择Deep[Top[x]] 较大的点x，修改x与top[x]间的各权值，再跳至Fa[top[x]]，直到U和V在同一条重链。

　　 while(Top[x]!=Top[y])
    {
        if(Deep[Top[x]]<Deep[Top[y]]) swap(x,y);
        对 Id[Top[x]] 到 Id[x] 进行操作
        x=Fa[Top[x]];
    }
    if(Deep[x]>Deep[y]) swap(x,y);
    对 Id[x] 到 Id[y] 进行操作

View Code

补：树剖求LCA

　　若两个点处在同一条重链上，深度低的那个就是LCA。

　　如果不在同一条重链上，那么就跟前面谈的修改操作一样，让两个点向上跳，直至它们在一条重链上（与上个操作类似）

例题：

1.【ZJOI2008】树的统计

问题描述：

一树上有 n 个节点，编号分别为 1 到 n，每个节点都有一个权值 w。我们将以下面的形式来要求你对这棵树完成一些操作：
　　CHANGE u t ：把节点 u 权值改为 t；
　　QMAX u v ：询问点 u 到点 v 路径上的节点的最大权值；
　　QSUM u v ：询问点 u 到点 v 路径上的节点的权值和。
注意：从点 u 到点 v 路径上的节点包括 u 和 v 本身。

输入格式：

第一行为一个数 n，表示节点个数；
接下来 n−1 行，每行两个整数 a,b，表示节点 a 与节点 b 之间有一条边相连；
接下来一行 n 个整数，第 i 个整数 wi 表示节点 i 的权值；
接下来一行，为一个整数 q ，表示操作总数；
接下来 q 行，每行一个操作，以 CHANGE u t 或 QMAX u v 或 QSUM u v的形式给出。

输出格式：

对于每个 QMAX 或 QSUM 的操作，每行输出一个整数表示要求的结果。

数据范围：

对于 100% 的数据 ，有 1≤n≤3×10e4,0≤q≤2×10e5 。中途操作中保证每个节点的权值 w 在 −30000 至 30000 之间。

　　板题，没有什么好讲的。单点修改 + 区间查询。

Code：

#pragma GCC optimize(2)
#pragma GCC optimize(3)
#include<bits/stdc++.h>
using namespace std;
char IP[7];
int n,Q,W[30005],Size[30005],Fa[30005],Son[30005],Deep[30005],Trans[30005],Id[30005],Top[30005],Cnt,Head[30005],Next[60005],To[60005];
struct node {int L,R,Max,Sum;}Tr[240005];
inline int read()
{
    int x(0),f(1);char ch=getchar();
    while(ch<'0'||ch>'9')
    {
        if(ch=='-') f=-1;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
    return f*x;
}
inline void ADD(int x,int y) {Next[++Cnt]=Head[x],Head[x]=Cnt,To[Cnt]=y,Next[++Cnt]=Head[y],Head[y]=Cnt,To[Cnt]=x;}
inline void DFS1(int x,int fa,int deep)
{
    int Max(0);
    Size[x]=1,Fa[x]=fa,Deep[x]=deep;
    for(register int i=Head[x],j;i;i=Next[i])
    {
        j=To[i];
        if(j==fa) continue;
        DFS1(j,x,deep+1),Size[x]+=Size[j];
        if(Size[j]>Max) Max=Size[j],Son[x]=j;
    }
}
inline void DFS2(int x,int anc)
{
    Top[x]=anc,Id[x]=++Cnt,Trans[Cnt]=x;
    if(Son[x]) DFS2(Son[x],anc);
    for(register int i=Head[x],j;i;i=Next[i])
    {
        j=To[i];
        if(j==Fa[x]||j==Son[x]) continue;
        DFS2(j,j);
    }
}
inline void Build(int x,int L,int R)
{
    Tr[x].L=L,Tr[x].R=R;
    if(L==R) {Tr[x].Sum=Tr[x].Max=W[Trans[L]];return;}
    int M=(L+R)>>1;
    Build(x<<1,L,M),Build(x<<1|1,M+1,R);
    Tr[x].Max=max(Tr[x<<1].Max,Tr[x<<1|1].Max),Tr[x].Sum=Tr[x<<1].Sum+Tr[x<<1|1].Sum;
}
inline void Modify(int x,int pos,int d)
{
    if(Tr[x].L==Tr[x].R) {Tr[x].Max=Tr[x].Sum=d;return;}
    if(pos<=Tr[x<<1].R) Modify(x<<1,pos,d);
    if(Tr[x<<1|1].L<=pos) Modify(x<<1|1,pos,d);
    Tr[x].Max=max(Tr[x<<1].Max,Tr[x<<1|1].Max),Tr[x].Sum=Tr[x<<1].Sum+Tr[x<<1|1].Sum;
}
inline int FindMax(int x,int L,int R)
{
    if(L<=Tr[x].L&&Tr[x].R<=R) return Tr[x].Max;
    int Lmax(-1000000000),Rmax(-1000000000);
    if(L<=Tr[x<<1].R) Lmax=FindMax(x<<1,L,R);
    if(Tr[x<<1|1].L<=R) Rmax=FindMax(x<<1|1,L,R);
    return max(Lmax,Rmax);
}
inline int FindSum(int x,int L,int R)
{
    if(L<=Tr[x].L&&Tr[x].R<=R) return Tr[x].Sum;
    int Lsum(0),Rsum(0);
    if(L<=Tr[x<<1].R) Lsum=FindSum(x<<1,L,R);
    if(Tr[x<<1|1].L<=R) Rsum=FindSum(x<<1|1,L,R);
    return Lsum+Rsum;
} 
inline int GetMax(int x,int y)
{
    int Max(-1000000000);
    while(Top[x]!=Top[y])
    {
        if(Deep[Top[x]]<Deep[Top[y]]) swap(x,y);
        Max=max(Max,FindMax(1,Id[Top[x]],Id[x])),x=Fa[Top[x]];
    }
    if(Deep[x]>Deep[y]) swap(x,y);
    Max=max(Max,FindMax(1,Id[x],Id[y]));
    return Max;
}
inline int GetSum(int x,int y)
{
    int Sum(0);
    while(Top[x]!=Top[y])
    {
        if(Deep[Top[x]]<Deep[Top[y]]) swap(x,y);
        Sum+=FindSum(1,Id[Top[x]],Id[x]),x=Fa[Top[x]]; 
    }
    if(Deep[x]>Deep[y]) swap(x,y);
    Sum+=FindSum(1,Id[x],Id[y]);
    return Sum;
}
int main()
{
    n=read();
    for(register int i=1,x,y;i<n;++i) x=read(),y=read(),ADD(x,y);
    for(register int i=1;i<=n;++i) W[i]=read();
    Cnt=0,DFS1(1,0,1),DFS2(1,1),Build(1,1,n);
    Q=read();
    for(register int i=1,x,y;i<=Q;++i)
    {
        scanf(" %s",IP),x=read(),y=read();
        switch(IP[1])
        {
            case 'H':{Modify(1,Id[x],y);break;}
            case 'M':{printf("%d\n",GetMax(x,y));break;}
            case 'S':{printf("%d\n",GetSum(x,y));break;}
        }
    }
    return 0;
}

【ZJOI2008】树的统计

2.【USACO 2011 Dec Gold 】种草

问题描述：

农夫约翰有N块贫瘠的牧场(2 <= N <= 100,000)，有N-1条双向道路将这N个牧场连接了起来，每两个牧场间都有且仅有一条路径可相互到达。著名奶牛贝西经常抱怨：为什么连接牧场的道路上没有草可吃呢?

约翰非常喜欢贝西，今天约翰终于决定要在道路上种草了。约翰的种草工作被分成了M(1 <= M <=100,000)步操作。
在每一步中，下列两个事件中的一个会发生：
1.约翰会选择两个牧场，沿着两个牧场间的路径,在路径上的每一条道路上都种植1株牧草；
2.贝西会向约翰提问：在一条指定的道路上，种植了多少株牧草；

请帮助约翰回答贝西的问题。

输入格式：

第一行，两个空格间隔的整数N和M
接下来N-1行，每行两个整数x和y，表示牧场x和y之间有道路直接相连
接下来M行，每行描述一步操作：
每行以字母P或Q作为开头，P代表种草操作，Q代表询问操作，接下来两个整数，A_i 和 B_i用于描述该步的操作(1 <= A_i, B_i <= N)。

输出格式：

对于每一次询问，输出一行，一个整数，表示询问的答案

　　也是板题，没有什么好讲的。区间修改 + 区间查询。

Code：

#pragma GCC optimize(2)
#pragma GCC optimize(3)
#include<bits/stdc++.h>
using namespace std;
char IP;
int n,Q,Size[100005],Fa[100005],Son[100005],Deep[100005],Trans[100005],Id[100005],Top[100005],Cnt,Head[100005],Next[200005],To[200005];
struct node {int L,R,V,Lazy;}Tr[800005];
inline int read()
{
    int x(0),f(1);char ch=getchar();
    while(ch<'0'||ch>'9')
    {
        if(ch=='-') f=-1;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
    return f*x;
}
inline void ADD(int x,int y) {Next[++Cnt]=Head[x],Head[x]=Cnt,To[Cnt]=y,Next[++Cnt]=Head[y],Head[y]=Cnt,To[Cnt]=x;}
inline void DFS1(int x,int fa,int deep)
{
    int Max(0);
    Size[x]=1,Fa[x]=fa,Deep[x]=deep;
    for(register int i=Head[x],j;i;i=Next[i])
    {
        j=To[i];
        if(j==fa) continue;
        DFS1(j,x,deep+1),Size[x]+=Size[j];
        if(Size[j]>Max) Max=Size[j],Son[x]=j;
    }
}
inline void DFS2(int x,int anc)
{
    Top[x]=anc,Id[x]=++Cnt,Trans[Cnt]=x;
    if(Son[x]) DFS2(Son[x],anc);
    for(register int i=Head[x],j;i;i=Next[i])
    {
        j=To[i];
        if(j==Fa[x]||j==Son[x]) continue;
        DFS2(j,j);
    }
}
inline void Build(int x,int L,int R)
{
    Tr[x].L=L,Tr[x].R=R;
    if(L==R) return;
    int M=(L+R)>>1;
    Build(x<<1,L,M),Build(x<<1|1,M+1,R);
}
inline void PutDown(int x) {Tr[x<<1].V+=Tr[x].Lazy,Tr[x<<1].Lazy+=Tr[x].Lazy,Tr[x<<1|1].V+=Tr[x].Lazy,Tr[x<<1|1].Lazy+=Tr[x].Lazy,Tr[x].Lazy=0;}
inline void ReModify(int x,int L,int R)
{
    if(L<=Tr[x].L&&Tr[x].R<=R) {++Tr[x].Lazy,++Tr[x].V;return;}
    if(Tr[x].Lazy) PutDown(x);
    if(L<=Tr[x<<1].R) ReModify(x<<1,L,R);
    if(Tr[x<<1|1].L<=R) ReModify(x<<1|1,L,R);
}
inline int FindSum(int x,int L,int R)
{
    if(L<=Tr[x].L&&Tr[x].R<=R) return Tr[x].V;
    if(Tr[x].Lazy) PutDown(x);
    int Lsum(0),Rsum(0);
    if(L<=Tr[x<<1].R) Lsum=FindSum(x<<1,L,R);
    if(Tr[x<<1|1].L<=R) Rsum=FindSum(x<<1|1,L,R);
    return Lsum+Rsum;
} 
inline void Modify(int x,int y)
{
    while(Top[x]!=Top[y])
    {
        if(Deep[Top[x]]<Deep[Top[y]]) swap(x,y);
        ReModify(1,Id[Top[x]],Id[x]),x=Fa[Top[x]];
    }
    if(x==y) return;
    if(Deep[x]>Deep[y]) swap(x,y);
    ReModify(1,Id[x]+1,Id[y]);
}
inline int GetSum(int x,int y)
{
    int V(0);
    while(Top[x]!=Top[y])
    {
        if(Deep[Top[x]]<Deep[Top[y]]) swap(x,y);
        V+=FindSum(1,Id[Top[x]],Id[x]),x=Fa[Top[x]]; 
    }
    if(x==y) return V;
    if(Deep[x]>Deep[y]) swap(x,y);
    V+=FindSum(1,Id[x]+1,Id[y]);
    return V;
}
int main()
{
    n=read(),Q=read();
    for(register int i=1,x,y;i<n;++i) x=read(),y=read(),ADD(x,y);
    Cnt=0,DFS1(1,0,1),DFS2(1,1),Build(1,1,n);
    for(register int i=1,x,y;i<=Q;++i)
    {
        scanf(" %1c",&IP),x=read(),y=read();
        switch(IP)
        {
            case 'P':{Modify(x,y);break;}
            case 'Q':{printf("%d\n",GetSum(x,y));break;}
        }
    }
    return 0;
}

【USACO 2011 Dec Gold 】种草

3.【SDOI2011 第1轮 DAY1】染色

问题描述：

给定一棵有个节点的无根树和m个操作，操作有2类：
1、将节点a到节点b路径上所有点都染成颜色c；
2、询问节点a到节点b路径上的颜色段数量（连续相同颜色被认为是同一段），如“112221”由3段组成：“11”、“222”和“1”。
请你写一个程序依次完成这m个操作。

输入格式：

第一行包含2个整数n和m，分别表示节点数和操作数；
第二行包含n个正整数表示n个节点的初始颜色
下面n-1行每行包含两个整数x和y，表示x和y之间有一条无向边。
下面m行每行描述一个操作：
“C a b c”表示这是一个染色操作，把节点a到节点b路径上所有点（包括a和b）都染成颜色；
“Q a b”表示这是一个询问操作，询问节点a到节点b（包括a和b）路径上的颜色段数量。

输出格式：

对于每个询问操作，输出一行答案。

数据范围：

1≤n≤10e5, 1≤m≤10e5 , 1≤c≤10e9

　　一眼看去，线段树对每一段记一下左边界和右边界的颜色，不就切了吗？

　　一交，WA了。

　　再一YY，上跳的时候出问题了：我们对 Id[Top[x]] 到 Id[x] 进行求和，再使 x = Fa[Top[x]] ，如果 Top[x] 和 Fa[Top[x]] 颜色一样，就算重了。我们只需再判一下就可以了（详见代码）。

Code：

#pragma GCC optimize(2)
#pragma GCC optimize(3)
#include<bits/stdc++.h>
using namespace std;
char IP;
int n,m,A[100005],Size[100005],Fa[100005],Son[100005],Deep[100005],Trans[100005],Id[100005],Top[100005],Cnt,Head[100005],Next[200005],To[200005];
struct node {int L,R,LC,RC,V,Lasy;}Tr[800005];
inline int read()
{
    int x(0),f(1);char ch=getchar();
    while(ch<'0'||ch>'9')
    {
        if(ch=='-') f=-1;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
    return f*x;
}
inline void ADD(int x,int y) {Next[++Cnt]=Head[x],Head[x]=Cnt,To[Cnt]=y,Next[++Cnt]=Head[y],Head[y]=Cnt,To[Cnt]=x;}
inline void DFS1(int x,int fa,int deep)
{
    int Max(0);
    Size[x]=1,Fa[x]=fa,Deep[x]=deep;
    for(register int i=Head[x],j;i;i=Next[i])
    {
        j=To[i];
        if(j==fa) continue;
        DFS1(j,x,deep+1),Size[x]+=Size[j];
        if(Size[j]>Max) Max=Size[j],Son[x]=j;
    }
}
inline void DFS2(int x,int anc)
{
    Top[x]=anc,Id[x]=++Cnt,Trans[Cnt]=x;
    if(Son[x]) DFS2(Son[x],anc);
    for(register int i=Head[x],j;i;i=Next[i])
    {
        j=To[i];
        if(j==Fa[x]||j==Son[x]) continue;
        DFS2(j,j);
    }
}
inline void Build(int x,int L,int R)
{
    Tr[x].L=L,Tr[x].R=R;
    if(L==R) {Tr[x].LC=Tr[x].RC=A[Trans[L]],Tr[x].V=1;return;}
    int M=(L+R)>>1;
    Build(x<<1,L,M),Build(x<<1|1,M+1,R),Tr[x].LC=Tr[x<<1].LC,Tr[x].RC=Tr[x<<1|1].RC,Tr[x].V=Tr[x<<1].V+Tr[x<<1|1].V-(Tr[x<<1].RC==Tr[x<<1|1].LC); 
}
inline void PutDown(int x) {Tr[x<<1].V=Tr[x<<1|1].V=1,Tr[x<<1].LC=Tr[x<<1].RC=Tr[x<<1].Lasy=Tr[x<<1|1].LC=Tr[x<<1|1].RC=Tr[x<<1|1].Lasy=Tr[x].Lasy,Tr[x].Lasy=0;}
inline void ReModify(int x,int L,int R,int z)
{
    if(L<=Tr[x].L&&Tr[x].R<=R) {Tr[x].LC=Tr[x].RC=Tr[x].Lasy=z,Tr[x].V=1;return;}
    if(Tr[x].Lasy) PutDown(x);
    if(L<=Tr[x<<1].R) ReModify(x<<1,L,R,z);
    if(Tr[x<<1|1].L<=R) ReModify(x<<1|1,L,R,z); 
    Tr[x].LC=Tr[x<<1].LC,Tr[x].RC=Tr[x<<1|1].RC,Tr[x].V=Tr[x<<1].V+Tr[x<<1|1].V-(Tr[x<<1].RC==Tr[x<<1|1].LC);
}
inline int FindAns(int x,int L,int R)
{
    if(L<=Tr[x].L&&Tr[x].R<=R) return Tr[x].V;
    if(Tr[x].Lasy) PutDown(x);
    int Lans(0),Rans(0),ans(0);
    if(L<=Tr[x<<1].R) Lans=FindAns(x<<1,L,R);
    if(Tr[x<<1|1].L<=R) Rans=FindAns(x<<1|1,L,R);
    ans=Lans+Rans;
    if(Lans&&Rans) ans-=(Tr[x<<1].RC==Tr[x<<1|1].LC); 
    return ans;
}
inline int Find(int x,int pos)
{
    if(Tr[x].Lasy) return Tr[x].Lasy;
    if(Tr[x].L==Tr[x].R) return Tr[x].LC;
    if(pos<=Tr[x<<1].R) return Find(x<<1,pos);
    return Find(x<<1|1,pos); 
}
inline void Modify(int x,int y,int z)
{
    while(Top[x]!=Top[y])
    {
        if(Deep[Top[x]]<Deep[Top[y]]) swap(x,y);
        ReModify(1,Id[Top[x]],Id[x],z),x=Fa[Top[x]];
    }
    if(Deep[x]>Deep[y]) swap(x,y);
    ReModify(1,Id[x],Id[y],z); 
}
inline int Lca(int x,int y)
{
    while(Top[x]!=Top[y])
    {
        if(Deep[Top[x]]<Deep[Top[y]]) swap(x,y);
        x=Fa[Top[x]]; 
    }
    if(Deep[x]>Deep[y]) swap(x,y);
    return x;
}
inline int GetAns(int x,int y)
{
    int Ans(0);
    while(Top[x]!=Top[y])
    {
        if(Deep[Top[x]]<Deep[Top[y]]) swap(x,y);
        Ans+=FindAns(1,Id[Top[x]],Id[x]);
        if(Find(1,Id[Fa[Top[x]]])==Find(1,Id[Top[x]])) --Ans;       //判断Fa[Top[x]] 和 Top[x] 是否同色
        x=Fa[Top[x]];
    }
    if(Deep[x]>Deep[y]) swap(x,y);
    Ans+=FindAns(1,Id[x],Id[y]);
    return Ans;
}
int main()
{
    n=read(),m=read();
    for(register int i=1;i<=n;++i) A[i]=read();
    for(register int i=1,x,y;i<n;++i) x=read(),y=read(),ADD(x,y);
    Cnt=0,DFS1(1,0,1),DFS2(1,1),Build(1,1,n);
    for(register int i=1,x,y,z;i<=m;++i)
    {
        scanf(" %1c",&IP);
        if(IP=='Q') x=read(),y=read(),printf("%d\n",GetAns(x,y));
        else x=read(),y=read(),z=read(),Modify(x,y,z);
    }
    return 0;
}

【SDOI2011 第1轮 DAY1】染色

4.【SDOI2014 R1D1】旅行

问题描述：

S国有N个城市，编号从1到N。城市间用N-1条双向道路连接，满足从一个城市出发可以到达其它所有城市。每个城市信仰不同的宗教，如飞天面条神教、隐形独角兽教、绝地教都是常见的信仰。为了方便，我们用不同的正整数代表各种宗教。
S国的居民常常旅行。旅行时他们总会走最短路，并且为了避免麻烦，只在信仰和他们相同的城市留宿。当然旅程的终点也是信仰与他相同的城市。S国政府为每个城市标定了不同的旅行评级，旅行者们常会记下途中（包括起点和终点）留宿过的城市的评级总和或最大值。
在S国的历史上常会发生以下几种事件：
• "CC x c"：城市x的居民全体改信了c教；
• "CW x w"：城市x的评级调整为w；
• "QS x y"：一位旅行者从城市x出发，到城市y，并记下了途中留宿过的城市的评级总和；
• "QM x y"：一位旅行者从城市x出发，到城市y，并记下了途中留宿过的城市的评级最大值。
由于年代久远，旅行者记下的数字已经遗失了，但记录开始之前每座城市的信仰与评级，还有事件记录本身是完好的。请根据这些信息，还原旅行者记下的数字。
为了方便，我们认为事件之间的间隔足够长，以致在任意一次旅行中，所有城市的评级和信仰保持不变。

输入格式：

输入的第一行包含整数N,Q，依次表示城市数和事件数。
接下来N行，第i+1行两个整数Wi,Ci依次表示记录开始之前，城市i的评级和信仰。
接下来N-1行每行两个整数x,y表示一条双向道路。
接下来Q行，每行一个操作，格式如上所述。

输出格式：

对每个QS和QM事件，输出一行，表示旅行者记下的数字。

数据范围：

1≤n≤10e5, 1≤m≤10e5 , 1≤c≤10e5

　　YY一会，可以想到，对每个宗教信仰开一颗线段树维护。但是，这样的话，我们要建10⁵棵线段树，每棵树有10⁵个点，敢交就敢AC。

　　怎么优化？？？很自然想到了“动态开点”，然后.........就没有然后了。

Code：

#pragma GCC optimize(2)
#pragma GCC optimize(3)
#include<bits/stdc++.h>
using namespace std;
char IP[3];
int n,Q,W[100005],C[100005],Size[100005],Fa[100005],Son[100005],Deep[100005],Trans[100005],Id[100005],Top[100005],Cnt,Head[100005],Next[200005],To[200005],tot,Root[100005];
struct node {int L,R,Ls,Rs,Sum,Max;}Tr[8000005];
inline int read()
{
    int x(0),f(1);char ch=getchar();
    while(ch<'0'||ch>'9')
    {
        if(ch=='-') f=-1;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
    return f*x;
}
inline void ADD(int x,int y) {Next[++Cnt]=Head[x],Head[x]=Cnt,To[Cnt]=y,Next[++Cnt]=Head[y],Head[y]=Cnt,To[Cnt]=x;}
inline void DFS1(int x,int fa,int deep)
{
    int Max(0);
    Size[x]=1,Fa[x]=fa,Deep[x]=deep;
    for(register int i=Head[x],j;i;i=Next[i])
    {
        j=To[i];
        if(j==fa) continue;
        DFS1(j,x,deep+1),Size[x]+=Size[j];
        if(Size[j]>Max) Max=Size[j],Son[x]=j;
    }
}
inline void DFS2(int x,int anc)
{
    Top[x]=anc,Id[x]=++Cnt,Trans[Cnt]=x;
    if(Son[x]) DFS2(Son[x],anc);
    for(register int i=Head[x],j;i;i=Next[i])
    {
        j=To[i];
        if(j==Fa[x]||j==Son[x]) continue;
        DFS2(j,j);
    }
}
inline void Modify(int &x,int L,int R,int pos,int d)
{
    if(!x) x=++tot,Tr[x].L=L,Tr[x].R=R;
    if(L==R) {Tr[x].Max+=d,Tr[x].Sum+=d;return;}
    int M=(L+R)>>1;
    if(pos<=M) Modify(Tr[x].Ls,L,M,pos,d);
    if(M<pos) Modify(Tr[x].Rs,M+1,R,pos,d);
    Tr[x].Max=max(Tr[Tr[x].Ls].Max,Tr[Tr[x].Rs].Max),Tr[x].Sum=Tr[Tr[x].Ls].Sum+Tr[Tr[x].Rs].Sum;
}
inline int FindSum(int x,int L,int R)
{
    if(L<=Tr[x].L&&Tr[x].R<=R) return Tr[x].Sum;
    int Lsum(0),Rsum(0);
    if(Tr[x].Ls&&L<=Tr[Tr[x].Ls].R) Lsum=FindSum(Tr[x].Ls,L,R);
    if(Tr[x].Rs&&Tr[Tr[x].Rs].L<=R) Rsum=FindSum(Tr[x].Rs,L,R);
    return Lsum+Rsum;
}
inline int FindMax(int x,int L,int R)
{
    if(L<=Tr[x].L&&Tr[x].R<=R) return Tr[x].Max;
    int Lmax(0),Rmax(0);
    if(Tr[x].Ls&&L<=Tr[Tr[x].Ls].R) Lmax=FindMax(Tr[x].Ls,L,R);
    if(Tr[x].Rs&&Tr[Tr[x].Rs].L<=R) Rmax=FindMax(Tr[x].Rs,L,R);
    return max(Lmax,Rmax);
}
inline void ReBelieve(int x,int y) {Modify(Root[C[x]],1,n,Id[x],-W[x]),C[x]=y,Modify(Root[C[x]],1,n,Id[x],W[x]);}
inline void Change(int x,int y) {Modify(Root[C[x]],1,n,Id[x],y-W[x]),W[x]=y;}
inline int GetSum(int x,int y,int z)
{
    int Sum(0);
    while(Top[x]!=Top[y])
    {
        if(Deep[Top[x]]<Deep[Top[y]]) swap(x,y);
        Sum+=FindSum(Root[z],Id[Top[x]],Id[x]),x=Fa[Top[x]];
    }
    if(Deep[x]>Deep[y]) swap(x,y);
    Sum+=FindSum(Root[z],Id[x],Id[y]);
    return Sum;
}
inline int GetMax(int x,int y,int z)
{
    int Max(0);
    while(Top[x]!=Top[y])
    {
        if(Deep[Top[x]]<Deep[Top[y]]) swap(x,y);
        Max=max(Max,FindMax(Root[z],Id[Top[x]],Id[x])),x=Fa[Top[x]];
    }
    if(Deep[x]>Deep[y]) swap(x,y);
    Max=max(Max,FindMax(Root[z],Id[x],Id[y]));
    return Max;
}
int main()
{
    n=read(),Q=read();
    for(register int i=1;i<=n;++i) W[i]=read(),C[i]=read();
    for(register int i=1,x,y;i<n;++i) x=read(),y=read(),ADD(x,y);
    Cnt=0,DFS1(1,0,1),DFS2(1,1);
    for(register int i=1;i<=n;++i) Modify(Root[C[i]],1,n,Id[i],W[i]);
    for(register int i=1,x,y;i<=Q;++i)
    {
        scanf(" %s",IP),x=read(),y=read();
        switch(IP[1])
        {
            case 'C':{ReBelieve(x,y);break;}
            case 'W':{Change(x,y);break;}
            case 'S':{printf("%d\n",GetSum(x,y,C[x]));break;}
            case 'M':{printf("%d\n",GetMax(x,y,C[x]));break;}
        }
    }
    return 0;
}

【SDOI2014 R1D1】旅行

5.魔法树

问题描述：

输入格式：

输出格式：

　　要求以 u 为根的子树中的点的总和，我们会想到 “DFS序”，再DFS一次，记下 In值和 Out值。但仔细想想，以 u 为根的子树中的点的 Id[ ] 一定是连续的，是从 Id[ u ] 开始到某个值的，所以，我们只需要记下子树中点 Id[ ] 的最大值就可以了（记在Som[ ]中），即 u 为根的子树中的点编号为从 Id[ u ] 到 Som[ u ]，再直接求就可以了。

Code：

#pragma GCC optimize(2)
#pragma GCC optimize(3)
#include<bits/stdc++.h>
using namespace std;
char IP[7];
int n,m,Size[100005],Fa[100005],Som[100005],Son[100005],Deep[100005],Trans[100005],Id[100005],Top[100005],Cnt,Head[100005],Next[100005],To[100005];
struct node {int L,R,Size,Lazy;long long V;}Tr[800005]; 
inline int read()
{
    int x(0),f(1);char ch=getchar();
    while(ch<'0'||ch>'9')
    {
        if(ch=='-') f=-1;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
    return f*x;
}
inline void ADD(int x,int y) {Next[++Cnt]=Head[x],Head[x]=Cnt,To[Cnt]=y;}
inline void DFS1(int x,int fa,int deep)
{
    int Max(0);
    Size[x]=1,Fa[x]=fa,Deep[x]=deep;
    for(register int i=Head[x],j;i;i=Next[i])
    {
        j=To[i],DFS1(j,x,deep+1),Size[x]+=Size[j];
        if(Size[j]>Max) Max=Size[j],Son[x]=j;
    }
}
inline void DFS2(int x,int anc)
{
    Top[x]=anc,Id[x]=++Cnt,Trans[Cnt]=x;
    if(Son[x]) DFS2(Son[x],anc);
    for(register int i=Head[x],j;i;i=Next[i])
    {
        j=To[i];
        if(j==Son[x]) continue;
        DFS2(j,j);
    }
    Som[x]=Cnt;
}
inline void Build(int x,int L,int R)
{
    Tr[x].L=L,Tr[x].R=R,Tr[x].Size=R-L+1;
    if(L==R) return;
    int M=(L+R)>>1;
    Build(x<<1,L,M),Build(x<<1|1,M+1,R); 
}
inline void PutDown(int x) {Tr[x<<1].V+=Tr[x<<1].Size*Tr[x].Lazy,Tr[x<<1].Lazy+=Tr[x].Lazy,Tr[x<<1|1].V+=Tr[x<<1|1].Size*Tr[x].Lazy,Tr[x<<1|1].Lazy+=Tr[x].Lazy,Tr[x].Lazy=0;}
inline void ReModify(int x,int L,int R,int d)
{
    if(L<=Tr[x].L&&Tr[x].R<=R) {Tr[x].V+=Tr[x].Size*d,Tr[x].Lazy+=d;return;}
    if(Tr[x].Lazy) PutDown(x);
    if(L<=Tr[x<<1].R) ReModify(x<<1,L,R,d);
    if(Tr[x<<1|1].L<=R) ReModify(x<<1|1,L,R,d);
    Tr[x].V=Tr[x<<1].V+Tr[x<<1|1].V;
}
inline long long GetAns(int x,int L,int R)
{
    if(L<=Tr[x].L&&Tr[x].R<=R) return Tr[x].V;
    if(Tr[x].Lazy) PutDown(x);
    long long Lans(0),Rans(0);
    if(L<=Tr[x<<1].R) Lans=GetAns(x<<1,L,R);
    if(Tr[x<<1|1].L<=R) Rans=GetAns(x<<1|1,L,R);
    return Lans+Rans; 
}
inline void Modify(int x,int y,int z)
{
    while(Top[x]!=Top[y])
    {
        if(Deep[Top[x]]<Deep[Top[y]]) swap(x,y);
        ReModify(1,Id[Top[x]],Id[x],z),x=Fa[Top[x]];
    }
    if(Deep[x]>Deep[y]) swap(x,y);
    ReModify(1,Id[x],Id[y],z);
}
int main()
{
    n=read();
    for(register int i=1,x,y;i<n;++i) x=read()+1,y=read()+1,ADD(x,y);
    Cnt=0,DFS1(1,0,1),DFS2(1,1),Build(1,1,n),m=read();
    for(register int i=1,x,y,z;i<=m;++i)
    {
        scanf(" %s",IP);
        if(IP[0]=='A') x=read()+1,y=read()+1,z=read(),Modify(x,y,z);
        else x=read()+1,printf("%lld\n",GetAns(1,Id[x],Som[x]));
    }
    return 0;
}

魔法树

5.遥远的国度

问题描述：

zcwwzdjn在追杀十分sb的zhx，而zhx逃入了一个遥远的国度。当zcwwzdjn准备进入遥远的国度继续追杀时，守护神RapiD阻拦了zcwwzdjn的去路，他需要zcwwzdjn完成任务后才能进入遥远的国度继续追杀。

问题是这样的：遥远的国度有n个城市，这些城市之间由一些路连接且这些城市构成了一颗树。这个国度有一个首都，我们可以把这个首都看做整棵树的根，但遥远的国度比较奇怪，首都是随时有可能变为另外一个城市的。遥远的国度的每个城市有一个防御值，有些时候RapiD会使得某两个城市之间的路径上的所有城市的防御值都变为某个值。RapiD想知道在某个时候，如果把首都看做整棵树的根的话，那么以某个城市为根的子树的所有城市的防御值最小是多少。由于RapiD无法解决这个问题，所以他拦住了zcwwzdjn希望他能帮忙。但zcwwzdjn还要追杀sb的zhx，所以这个重大的问题就被转交到了你的手上。

输入格式：

第1行两个整数n m，代表城市个数和操作数。
第2行至第n行，每行两个整数 u v，代表城市u和城市v之间有一条路。
第n+1行，有n个整数，代表所有点的初始防御值。
第n+2行一个整数 id，代表初始的首都为id。
第n+3行至第n+m+2行，首先有一个整数opt，如果opt=1，接下来有一个整数id，代表把首都修改为id；如果opt=2，接下来有三个整数p1 p2 v，代表将p1 p2路径上的所有城市的防御值修改为v；如果opt=3，接下来有一个整数 id，代表询问以城市id为根的子树中的最小防御值。

输出格式：

对于每个opt=3的操作，输出一行代表对应子树的最小点权值。

数据范围：

对于100%的数据，n<=100000，m<=100000，0<所有权值<=2^31。

　　（一道好题）

　　首先，要求以 id 为子树中的点的最小值，这和上道题一样，就不在赘述了。

　　下面，我们来解决“换根” 这一神犇操作：

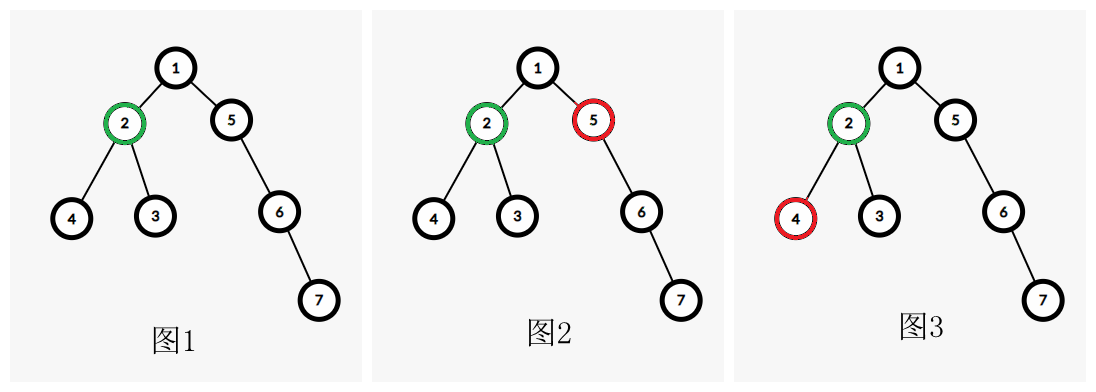
　　　　我们对2号点进行讨论：

　　　　　　情况a：新根不在2的子树中（如图2），那么对答案并无影响；

　　　　　　情况b：新根在2的子树中（如图3），那么答案应为整棵树除去2号点往4号点方向的子树中的最小值。

　　　　由此观之，换根不用真正换根，只要存在在思想中就可以了。

　　但好像问题由来了：怎么除去2号点往4号点方向的子树？

　　我们要充分利用树链剖分中 Id 的连续性质和上跳的操作，求出2号点向4号点方向的第一个点（设为root），就可以知道整棵子树，让4号点往上跳到 Top[ x ] == Top[ y ]，并在修改 x 前记下 Last = Top [ x ]；如果此时，x == y ，那么 root = Last；否则，y 一定是从 x 的重儿子来，所以 root = Som[ x ] （Som[ x ] 为x 的重儿子）。所以，我们要求的区间为 [ 1 , Id [ root ] ) & ( Som[ root ] , n ]。

　　最后，int 的最大值是 2^31 - 1，所以，要开long long ! 要开long long ! 要开long long !

Code：

#pragma GCC optimize(2)
#pragma GCC optimize(3)
#include<bits/stdc++.h>
using namespace std;
int n,m,Root,Size[500005],Fa[500005],Som[500005],Son[500005],Deep[500005],Trans[500005],Id[500005],Top[500005],Cnt,Head[500005],Next[1000005],To[1000005];
long long D[500005];
struct node {int L,R,Size;long long Min,Lazy;}Tr[1000005];
#define gc (p1==p2&&(p2=(p1=buf)+fread(buf,1,65536,stdin),p1==p2)?EOF:*p1++)
char buf[65536],*p1,*p2;
inline int read()
{
    char ch;int x(0);
    while((ch=gc)<48);
    do x=x*10+ch-48;while((ch=gc)>=48);
    return x;
}
inline long long lread()
{
    char ch;long long x(0);
    while((ch=gc)<48);
    do x=x*10+ch-48;while((ch=gc)>=48);
    return x;
}
inline void ADD(int x,int y) {Next[++Cnt]=Head[x],Head[x]=Cnt,To[Cnt]=y,Next[++Cnt]=Head[y],Head[y]=Cnt,To[Cnt]=x;}
inline void DFS1(int x,int fa,int deep)
{
    int Max(0);
    Size[x]=1,Fa[x]=fa,Deep[x]=deep;
    for(register int i=Head[x],j;i;i=Next[i])
    {
        j=To[i];
        if(j==fa) continue;
        DFS1(j,x,deep+1),Size[x]+=Size[j];
        if(Size[j]>Max) Max=Size[j],Son[x]=j;
    }
}
inline void DFS2(int x,int anc)
{
    Top[x]=anc,Id[x]=++Cnt,Trans[Cnt]=x;
    if(Son[x]) DFS2(Son[x],anc);
    for(register int i=Head[x],j;i;i=Next[i])
    {
        j=To[i];
        if(j==Son[x]||j==Fa[x]) continue;
        DFS2(j,j);
    }
    Som[x]=Cnt;
}
inline void Build(int x,int L,int R)
{
    Tr[x].L=L,Tr[x].R=R,Tr[x].Size=R-L+1;
    if(L==R) {Tr[x].Min=D[Trans[L]];return;}
    int M=(L+R)>>1;
    Build(x<<1,L,M),Build(x<<1|1,M+1,R),Tr[x].Min=min(Tr[x<<1].Min,Tr[x<<1|1].Min);
}
inline void PutDown(int x) {Tr[x<<1].Min=Tr[x<<1].Lazy=Tr[x<<1|1].Min=Tr[x<<1|1].Lazy=Tr[x].Lazy,Tr[x].Lazy=0;}
inline void ReModify(int x,int L,int R,int d)
{
    if(L<=Tr[x].L&&Tr[x].R<=R) {Tr[x].Min=Tr[x].Lazy=d;return;}
    if(Tr[x].Lazy) PutDown(x);
    if(L<=Tr[x<<1].R) ReModify(x<<1,L,R,d);
    if(Tr[x<<1|1].L<=R) ReModify(x<<1|1,L,R,d);
    Tr[x].Min=min(Tr[x<<1].Min,Tr[x<<1|1].Min);
}
inline long long FindMin(int x,int L,int R)
{
    if(L<=Tr[x].L&&Tr[x].R<=R) return Tr[x].Min;
    if(Tr[x].Lazy) PutDown(x);
    long long Lmin(1000000000000000),Rmin(1000000000000000);
    if(L<=Tr[x<<1].R) Lmin=FindMin(x<<1,L,R);
    if(Tr[x<<1|1].L<=R) Rmin=FindMin(x<<1|1,L,R);
    return min(Lmin,Rmin);
}
inline void Modify(int x,int y,int z)
{
    while(Top[x]!=Top[y])
    {
        if(Deep[Top[x]]<Deep[Top[y]]) swap(x,y);
        ReModify(1,Id[Top[x]],Id[x],z),x=Fa[Top[x]];
    }
    if(Deep[x]>Deep[y]) swap(x,y);
    ReModify(1,Id[x],Id[y],z);
}
inline long long GetMin(int x)
{
    if(Id[Root]<Id[x]||Som[x]<Id[Root]) return FindMin(1,Id[x],Som[x]);
    if(Root==x) return Tr[1].Min;
    int root(Root),Last;
    long long Lmin(1000000000000000),Rmin(1000000000000000);
    while(Top[x]!=Top[root]) Last=Top[root],root=Fa[Top[root]];
    if(root==x) root=Last;else root=Son[x];
    if(1<=Id[root]-1) Lmin=FindMin(1,1,Id[root]-1);
    if(Som[root]+1<=Som[1]) Rmin=FindMin(1,Som[root]+1,Som[1]);
    return min(Lmin,Rmin);
}
signed main()
{
    n=read(),m=read();
    for(register int i=1,x,y;i<n;++i) x=read(),y=read(),ADD(x,y);
    for(register int i=1;i<=n;++i) D[i]=lread();
    Cnt=0,DFS1(1,0,1),DFS2(1,1),Build(1,1,n),Root=read();
    for(register int i=1,opt,x,y,z;i<=m;++i)
    {
        opt=read();
        switch(opt)
        {
            case 1:{Root=read();break;}
            case 2:{x=read(),y=read(),z=lread(),Modify(x,y,z);break;}
            case 3:{x=read(),printf("%lld\n",GetMin(x));break;}
        }
    }
    return 0;
}

遥远的国度

文末有......

有.......

有nodgd:

posted @ 2021-07-27 20:01 qfxl 阅读(307) 评论(1) 收藏举报

刷新页面返回顶部

qfxl

No man ever steps in the same river twice.

树链剖分

公告