2021.7.17 NKOJ周赛总结

　　发现自己简直是个智障：T1模数写成1e9+9；T2居然没有考虑刚好一个周期的情况；T4用“%lld”读入“unsigned long long”。~qwq~

T1: 跳马（nkoj 8374）

问题描述:

果果上课觉得无聊，于是掏出一枚中国象棋中的"马"棋子开始玩了起来。

中国象棋中的"马"走 "日" 字，即横坐标跳1、纵坐标跳2，或者横坐标跳2，纵坐标跳1。

果果把"马"放在一个二维网格棋盘的左下角坐标为(0, 0)，并且选定了一个终点(n, m)，果果想知道，有多少种不同的方案可以让"马"走到终点？

果果不喜欢走回头路，因此每经过一次跳跃，横纵坐标都要离目标更近。

输入格式:

第 1 行输入 2 个整数 n,m。

输出格式:

输出 1 行 1 个整数，表示从(0,0) 跳到 (n, m) 的方案数对 109+7 取模。

数据范围：

对于 30% 的数据 0≤n,m≤500
对于 100% 的数据 0≤n,m≤10e5

　　“每经过一次跳跃，横纵坐标都要离目标更近”，画画图很容易发现“马”的路线为下图：

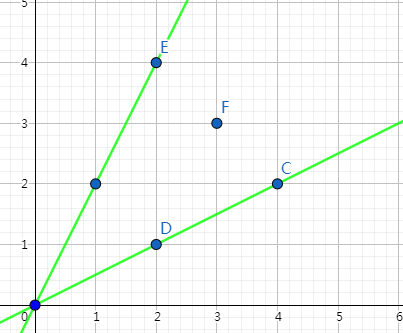
　　易得：“马”能到的地方： (n+m)%3==0 && 0.5<=n/m<=2；

　　各个合法位置的方案数为：

显然是个“杨辉三角”，用组合数求出即可。

T2: 果苣之手(nkoj 8375)

问题描述:

俗话说：“果苣在手，天下我有”。而拥有果苣之手的你，决定当一个无情的发牌员。

一副牌有 n 张，编号为 1,2,...,n 。初始时牌按编号顺序排列，即位于 i 号位置的牌恰好是 i 号牌。为了公平，发牌前要先洗牌。果苣之手的特性决定了单次洗牌的规律，当一次洗牌结束后，原本位于位置 i 的牌被洗到了 pi，而 p1,p2,...,pn 构成了一个排列 。果苣之手还决定了你必须要重复洗牌 m 次。

请拥有果苣之手的你完成洗牌并输出洗牌后牌的顺序。

输入格式:

第 1 行输入 1 个整数 n。 第 2 行输入 1 个整数 m。 第 3 行输入 n 个整数 pi。

输出格式:

输出 1 行 n 个数，表示洗牌后牌的顺序。

数据范围:

1≤n≤10e5
0≤m≤10e100000
1≤pi≤n 且 p1,p2,...,pn 构成排列

对于 20% 的数据，1≤n,m≤1000

对于 70% 的数据，1≤m≤10e9

　　首先，在洗一定次数后，一定会和原状态相同，即会成“环”，很容易就想到用并查集(老板最爱)对每个环进行处理；

　　但要注意那个 m 的范围，太巨大了，高精模了解一下：

#pragma GCC optimize(2)
#pragma GCC optimize(3)
#include<bits/stdc++.h>
using namespace std;
string a;
int b;
inline int Mod(string a,int b)
{
    int d=0;
    for(int i=0;i<a.size();i++)  d=(d*10+(a[i]-'0'))%b;
    return d;
}
int main()
{
    ios::sync_with_stdio(false);
    cin>>a>>b,cout<<Mod(a,b)<<endl;
    return 0;
}

　　code:

#pragma GCC optimize(2)
#pragma GCC optimize(3)
#include<bits/stdc++.h>
using namespace std;
string m;
int n,head,tail,MM[100005],Q[200005],P[100005],Fa[100005],Size[100005],Ans[100005];
inline int Mod(string a,int b)
{
    if(MM[b]) return MM[b];
    int d=0;
    for(register int i=0;i<a.size();++i)  d=((d<<3)+(d<<1)+(a[i]-'0'))%b;
    return MM[b]=d;
}
inline int GetF(int x)
{
    if(x==Fa[x]) return x;
    return Fa[x]=GetF(Fa[x]);
}
int main()
{
    ios::sync_with_stdio(false);
    cin>>n>>m;
    for(register int i=1;i<=n;++i) Fa[i]=i,Size[i]=1,Ans[i]=i;
    for(register int i=1,fx,fy;i<=n;++i)
    {
        cin>>P[i],fx=GetF(i),fy=GetF(P[i]);
        if(fx!=fy) Fa[fy]=fx,Size[fx]+=Size[fy];
    }
    for(register int i=1,j,x,fa;i<=n;++i)
    {
        fa=GetF(i);
        if(!Size[fa]) continue;
        j=Mod(m,Size[fa]),head=tail=0,x=i;
        if(!j) {Size[fa]=0;continue;}
        while(j) Q[++head]=x,x=P[x],--j;
        while(Size[fa]) Ans[x]=Q[++tail],Q[++head]=x,x=P[x],--Size[fa];
    }
    for(register int i=1;i<=n;++i) cout<<Ans[i]<<" ";
    return 0;
}

T3: 平方数(nkoj 8376)

（待更）(下辈子一定更)(可看 kzsn 博客 ,记得举报低俗内容哦)

T4: 简单模板水题(nkoj 8377)

问题描述:

经过一段时间的学习，果果发现很多题都是很简单的模板水题，比如下面这题。

有一个长度为 n 的数列 a1,a2,...,an，初值全为 0。

我们要对这个数列进行 m 次如下操作：

选择一个连续子数列 al,al+1,...,ar(l≤r)，将其中小于 vi 的值全部修改为 vi
求 m 次操作后的数组。

输入格式:

第 1 行输入 2 个整数 n,m，表示数组长度和操作次数。 第 2 行输入 3 个整数 x,y,z 作为参数，用于生成 m 次操作的数据。

unsigned long long x, y, z;
inline unsigned long long RNG() {
    x ^= x << 16;
    x ^= x >> 5;
    x ^= x << 1;
    unsigned long long w = x ^ y ^ z;
    x = y;
    y = z;
    z = w;
    return z;
}
生成方式如下：

连续调用 RNG 函数 3 次，得到 r1,r2,r3
li=min(r1%n,r2%n)+1
ri=max(r1%n,r2%n)+1
vi=r3%230
总共调用 3m 次，就能获得 m 次操作的所有数据。

输出格式:

输出 1 行 n 个数，表示 m 次操作后的数组。

数据范围:

1≤n≤105
1≤m≤107
0≤x,y,z<2e64

对于 20% 的数据，1≤n,m≤10e3

对于 80% 的数据，1≤m≤10e5

　　首先YY一哈这个东西：

unsigned long long x, y, z;
inline unsigned long long RNG() {
    x ^= x << 16;
    x ^= x >> 5;
    x ^= x << 1;
    unsigned long long w = x ^ y ^ z;
    x = y;
    y = z;
    z = w;
    return z;
}

　　这个类似于随机（即 rand()），周期很大；

　　这道题的正解是ST表（O(m+n log n)），但线段树也能过，由于太菜了，所以当时只想到了线段树，去维护区间的最小值就好了，修改+遍历，是O(m log n+n long n)的；

　　然后自己把线段树魔改了一下(莫名就比ST表快了，和数据有关，理论上线段树应该比ST慢)。

　　code：

#pragma GCC optimize(2)
#pragma GCC optimize(3)
#include<bits/stdc++.h>
#define mod 1073741824
using namespace std;
int n,m,Ans[100005];
unsigned long long x,y,z;
struct node{int L,R,V;}Tree[800005];
inline unsigned long long RNG()
{
    x^=x<<16,x^=x>>5,x^=x<<1;
    unsigned long long w=x^y^z;
    x=y,y=z,z=w;
    return z;
}
inline void Build(int p,int L,int R)
{
    Tree[p].L=L,Tree[p].R=R;
    if(L==R) return;
    int M=(L+R)>>1;
    Build(p<<1,L,M),Build(p<<1|1,M+1,R);
}
inline void PutDown(int p) {Tree[p<<1].V=max(Tree[p<<1].V,Tree[p].V),Tree[p<<1|1].V=max(Tree[p<<1|1].V,Tree[p].V);}
inline void modify(int p,int L,int R,int d)
{
    if(Tree[p].V>=d) return;
    if(L<=Tree[p].L&&Tree[p].R<=R) {Tree[p].V=d;return;}
    PutDown(p);
    int M=(Tree[p].L+Tree[p].R)>>1;
    if(L<=M&&R>=Tree[p<<1].L) modify(p<<1,L,R,d);
    if(R>M&&L<=Tree[p<<1|1].R) modify(p<<1|1,L,R,d);
    Tree[p].V=min(Tree[p<<1].V,Tree[p<<1|1].V);
}
inline void getSum(int p)
{
    if(Tree[p].L==Tree[p].R) {Ans[Tree[p].L]=Tree[p].V;return;}
    PutDown(p),getSum(p<<1),getSum(p<<1|1);
}
int main()
{
    scanf("%d%d%llu%llu%llu",&n,&m,&x,&y,&z),Build(1,1,n);
    for(register int i=1;i<=m;++i)
    {
        int r1=RNG()%n,r2=RNG()%n,V=RNG()%mod,L=min(r1,r2)+1,R=max(r1,r2)+1;
        modify(1,L,R,V);
    }
    getSum(1);
    for(register int i=1;i<=n;++i) printf("%d ",Ans[i]);
    return 0;
}

　　最后，强烈建议T3 ,T4 换位子。

posted @ 2021-07-19 16:51 qfxl 阅读(211) 评论(1) 收藏举报

刷新页面返回顶部

qfxl

No man ever steps in the same river twice.

2021.7.17 NKOJ周赛总结

公告