P3953 逛公园
Description
策策同学特别喜欢逛公园。公园可以看成一张N个点M条边构成的有向图,且没有 自环和重边。其中1号点是公园的入口,N号点是公园的出口,每条边有一个非负权值, 代表策策经过这条边所要花的时间。
策策每天都会去逛公园,他总是从1号点进去,从N号点出来。
策策喜欢新鲜的事物,它不希望有两天逛公园的路线完全一样,同时策策还是一个 特别热爱学习的好孩子,它不希望每天在逛公园这件事上花费太多的时间。如果1号点 到NN号点的最短路长为dd,那么策策只会喜欢长度不超过d+K的路线。
策策同学想知道总共有多少条满足条件的路线,你能帮帮它吗?
为避免输出过大,答案对PP取模。
如果有无穷多条合法的路线,请输出-1。
Solution1:
参考了题解 P3953 【逛公园】可能是长沙一位大佬的题解.
不过我选择吐槽一下他的代码可读性.
虽然我优化了一遍把可读性优化没了不少吧!
😄
没有零边
首先考虑没有零环的情况, 这时候只需要用一个类似于最短路计数的做法.
首先求出 1 号点到所有点的最短路.
用\(f(u,j)\)表示从一到\(u\)的所有路径中等于\(dis_u+j\)的有多少条.
\(f(u,j)\)可以转移到\(f(v,dis_u + c + j - dis_v)\)
如果存在边\((u, v)\)且边权为\(c\)的话.
这样的话需要先更新\(dis\)小的点.
对了, 注意转移的枚举顺序, 先枚举\(j\), 再枚举$$
优化
需要优化的呀!
因为会超时的呀!
所以我就优化了一上午
- 内存池开好
- 手写
pair<int, int> - zkw线段树优化dijkstra
- 读入优化
- 把所有的
delete语句, 析构函数都删了, 因为完全是在挥霍内存, 实际中这样玩是会被骂死的.
写完之后又随便封装了一下子, 现在没那么鬼畜了.
可读性应该还行吧.
ZKW线段树参考了这里
Code
一开始的代码和优化后的代码:
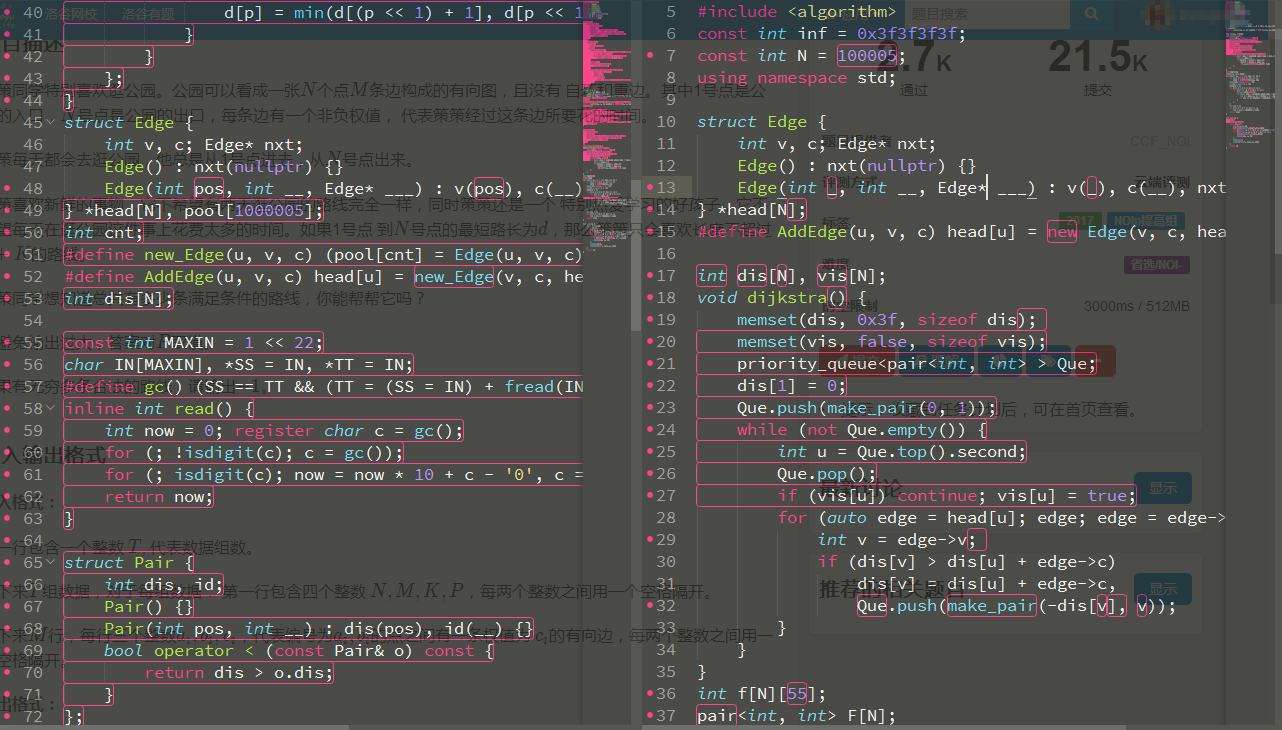
#include <math.h>
#include <queue>
#include <stdio.h>
#include <string.h>
#include <iostream>
#include <algorithm>
const int inf = 0x3f3f3f3f;
const int N = 100001;
using namespace std;
struct Pair {
int dis, id;
Pair() {}
Pair(int pos, int __) : dis(pos), id(__) {}
bool operator < (const Pair& o) const {
return dis > o.dis;
}
};
#define Online
namespace {
struct Node {
int v; int id;
Node() { }
Node(int _value): v(_value) {}
Node(int _, int __) : v(_), id(__) {}
bool operator < (const Node& o) const {
return v < o.v;
}
};
class Heap {
private:
Node *d; int n;
public:
Heap(int _MaxN) {
n = 1 << (1 + (int) (log(_MaxN) / log(2.0)));
d = new Node[n << 1];
for (int i = 1; i <= n + n - 1; i++)
d[i] = Node(inf, i - n + 1);
for (int i = 1; i <= n + n - 1; i++)
d[i] = Node(inf, i >= n ? i - n + 1 : 0);
}
~Heap() { }
inline int top_pos() {
return d[1].id;
}
inline void modify(int pos, int s) {
int p = pos + n - 1;
d[p].v = s;
while (p) {
p >>= 1,
d[p] = min(d[(p << 1) + 1], d[p << 1]);
}
}
};
} // Heap
namespace {
const int MAXIN = 1 << 22;
char IN[MAXIN], *SS = IN, *TT = IN;
#ifdef Online
#define gc() (SS == TT && (TT = (SS = IN) + fread(IN, 1, MAXIN, stdin), SS == TT) ? EOF : *SS++)
#else
#define gc() getchar()
#endif
inline int read() {
int now = 0; register char c = gc();
for (; !isdigit(c); c = gc());
for (; isdigit(c); now = now * 10 + c - '0', c = gc());
return now;
}
} // Read
namespace {
struct Edge {
int v, c; Edge* nxt;
Edge() : nxt(nullptr) {}
Edge(int pos, int __, Edge* ___) : v(pos), c(__), nxt(___) {}
} pool[1000005];
int cnt;
#define new_Edge(u, v, c) (pool[cnt] = Edge(u, v, c), &pool[cnt++])
} // Edge
class Graph {
public:
int n;
Edge* head[N];
Graph() {}
~Graph() {
}
inline void AddEdge(int u, int v, int c) {
head[u] = new_Edge(v, c, head[u]);
}
};
class Solution : public Graph {
int f[N][51];
Pair F[N];
public:
Solution(int _) {
n = _;
for (int i = 0; i <= n; i += 1) head[i] = nullptr;
}
~Solution() {
}
int dis[N];
void dijkstra(int s) {
Heap* T = new Heap(n + 1);
memset(dis, 0x3f, sizeof dis);
dis[s] = 0, T->modify(s, 0);
for (int i = 1; i <= n; i += 1) {
int u = T->top_pos();
T->modify(u, inf);
for (auto edge = head[u]; edge; edge = edge->nxt) {
int v = edge->v;
if (dis[v] > dis[u] + edge->c)
dis[v] = dis[u] + edge->c,
T->modify(v, dis[u] + edge->c);
}
}
}
int Solve(int k, const int mod) {
dijkstra(1);
for (int i = 1; i <= n; i += 1)
F[i] = Pair(-dis[i], i);
memset(f, false, sizeof f);
sort(F + 1, F + n + 1);
f[1][0] = 1;
for (int j = 0; j <= k; j += 1) {
for (int i = 1; i <= n; i += 1) {
int u = F[i].id;
if (not f[u][j]) continue;
for (auto edge = head[u]; edge; edge = edge->nxt) {
int v = edge->v, ly = dis[u] + j + edge->c - dis[v];
if (ly <= k) f[v][ly] = (f[v][ly] + f[u][j]) % mod;
}
}
}
int res = 0;
for (int i = 0; i <= k; i += 1)
res = (res + f[n][i]) % mod;
return res;
}
};
int main () {
int T = read();
while (T--) {
int n, m, k, p;
n = read(), m = read(), k = read(), p = read();
Solution* G = new Solution(n);
for (int i = 0, u, v, c; i < m; i += 1) {
u = read(), v = read(), c = read();
G->AddEdge(u, v, c);
}
printf("%d\n", G->Solve(k, p));
}
return 0;
}
处理零边
将边权为0的边加入新图, 拓扑排序完入度不为0的点位于零环上.
当\(dis_{1, k} + dis_{n,k} > dis_{1, n} + n\)的话且\(k\)位于零环上的话, 输出-1
可是我没有建反图直接求\(dis_{n,k}\)的呀! 竟然还过了???????数据是不是有点水的呀!
然后按第一关键字\(dis_{1, u}\)第二关键字拓扑序排序动态规划就可以了.
Code
#include <math.h>
#include <queue>
#include <stdio.h>
#include <string.h>
#include <iostream>
#include <algorithm>
const int inf = 0x3f3f3f3f;
const int N = 100001;
using namespace std;
struct Pair {
int dis, id;
Pair() {}
Pair(int pos, int __) : dis(pos), id(__) {}
bool operator < (const Pair& o) const {
return dis > o.dis;
}
};
struct Pair_pro {
int dis, top, id;
Pair_pro() {}
Pair_pro(int _, int __, int ___) :
dis(_), top(__), id(___) {}
bool operator < (const Pair_pro& o) const {
return dis == o.dis ? top < o.top : dis < o.dis;
}
};
#define Online
namespace {
struct Node {
int v; int id;
Node() { }
Node(int _value): v(_value) {}
Node(int _, int __) : v(_), id(__) {}
bool operator < (const Node& o) const {
return v < o.v;
}
};
class Heap {
private:
Node *d; int n;
public:
Heap(int _MaxN) {
n = 1 << (1 + (int) (log(_MaxN) / log(2.0)));
d = new Node[n << 1];
for (int i = 1; i <= n + n - 1; i++)
d[i] = Node(inf, i - n + 1);
for (int i = 1; i <= n + n - 1; i++)
d[i] = Node(inf, i >= n ? i - n + 1 : 0);
}
~Heap() { }
inline int top_pos() {
return d[1].id;
}
inline void modify(int pos, int s) {
int p = pos + n - 1;
d[p].v = s;
while (p) {
p >>= 1,
d[p] = min(d[(p << 1) + 1], d[p << 1]);
}
}
};
} // Heap
namespace {
const int MAXIN = 1 << 22;
char IN[MAXIN], *SS = IN, *TT = IN;
#ifdef Online
#define gc() (SS == TT && (TT = (SS = IN) + fread(IN, 1, MAXIN, stdin), SS == TT) ? EOF : *SS++)
#else
#define gc() getchar()
#endif
inline int read() {
int now = 0; register char c = gc();
for (; !isdigit(c); c = gc());
for (; isdigit(c); now = now * 10 + c - '0', c = gc());
return now;
}
} // Read
namespace {
struct Edge {
int v, c; Edge* nxt;
Edge() : nxt(nullptr) {}
Edge(int pos, int __, Edge* ___) : v(pos), c(__), nxt(___) {}
} pool[1000005];
int cnt;
#define new_Edge(u, v, c) (pool[cnt] = Edge(u, v, c), &pool[cnt++])
} // Edge
class Graph {
public:
int n;
Edge* head[N];
Graph() {}
~Graph() {
}
inline void AddEdge(int u, int v, int c) {
head[u] = new_Edge(v, c, head[u]);
}
};
class SolveZeroLoop : public Graph {
int du[N];
public:
inline void AddEdge(int u, int v, int c) {
head[u] = new_Edge(v, c, head[u]);
du[v] += 1;
}
SolveZeroLoop(int _) {
n = _;
for (int i = 0; i <= n; i += 1) head[i] = nullptr;
for (int i = 0; i <= n; i += 1) du[i] = 0;
}
const int* topsort(const int* d1, const int* dn, const int& k) {
int* array = new int[n + 1];
queue<int> que;
int t = 0;
for (int i = 1; i <= n; i += 1)
if (not du[i]) que.push(i), array[i] = t++;
while (not que.empty()) {
int u = que.front(); que.pop();
for (auto edge = head[u]; edge; edge = edge->nxt) {
if (not --du[edge->v]) que.push(edge->v), array[edge->v] = t++;
}
}
for (int i = 1; i <= n; i += 1)
if (du[i] and d1[i] + dn[i] <= k + d1[n]) return nullptr;
return (const int *) array;
}
};
class Solution : public Graph {
int f[N][51];
Pair_pro F[N];
public:
Solution(int _) {
n = _;
for (int i = 0; i <= n; i += 1) head[i] = nullptr;
}
void dijkstra(int s, int* dis) {
Heap* T = new Heap(n + 1);
for (int i = 2; i <= n; i += 1) dis[i] = inf;
dis[s] = 0, T->modify(s, 0);
for (int i = 1; i <= n; i += 1) {
int u = T->top_pos();
T->modify(u, inf);
for (auto edge = head[u]; edge; edge = edge->nxt) {
int v = edge->v;
if (dis[v] > dis[u] + edge->c)
dis[v] = dis[u] + edge->c,
T->modify(v, dis[u] + edge->c);
}
}
}
int Solve(const int k, const int mod, SolveZeroLoop* oG) {
int *d1 = new int[n + 1], *d2 = new int[n + 1];
dijkstra(1, d1), dijkstra(n, d2);
const int *top = oG->topsort(d1, d2, k);
if (top == nullptr) return -1;
for (int i = 1; i <= n; i += 1)
F[i] = Pair_pro(d1[i], top[i], i);
memset(f, false, sizeof f);
sort(F + 1, F + n + 1);
f[1][0] = 1;
for (int j = 0; j <= k; j += 1) {
for (int i = 1; i <= n; i += 1) {
int u = F[i].id;
if (not f[u][j]) continue;
for (auto edge = head[u]; edge; edge = edge->nxt) {
int v = edge->v, ly = d1[u] + j + edge->c - d1[v];
if (ly <= k) f[v][ly] = (f[v][ly] + f[u][j]) % mod;
}
}
}
int res = 0;
for (int i = 0; i <= k; i += 1)
res = (res + f[n][i]) % mod;
return res;
}
};
int main () {
int T = read();
while (T--) {
int n, m, k, p;
n = read(), m = read(), k = read(), p = read();
Solution* G = new Solution(n);
SolveZeroLoop* oG = new SolveZeroLoop(n);
for (int i = 0, u, v, c; i < m; i += 1) {
u = read(), v = read(), c = read();
G->AddEdge(u, v, c);
if (not c) oG->AddEdge(u, v, c);
}
printf("%d\n", G->Solve(k, p, oG));
}
return 0;
}
内存泄露
顺便试了一下新学的智能指针.
还行吧.
解决了内存泄露问题
// luogu-judger-enable-o2
#include <math.h>
#include <queue>
#include <memory>
#include <stdio.h>
#include <string.h>
#include <iostream>
#include <algorithm>
const int inf = 0x3f3f3f3f;
const int N = 100001;
using namespace std;
struct Pair {
int dis, id;
Pair() {}
Pair(int pos, int __) : dis(pos), id(__) {}
bool operator < (const Pair& o) const {
return dis > o.dis;
}
};
struct Pair_pro {
int dis, top, id;
Pair_pro() {}
Pair_pro(int _, int __, int ___) :
dis(_), top(__), id(___) {}
bool operator < (const Pair_pro& o) const {
return dis == o.dis ? top < o.top : dis < o.dis;
}
};
#define Online
namespace {
struct Node {
int v; int id;
Node() { }
Node(int _value): v(_value) {}
Node(int _, int __) : v(_), id(__) {}
bool operator < (const Node& o) const {
return v < o.v;
}
};
class Heap {
private:
Node *d; int n;
public:
Heap(int _MaxN) {
n = 1 << (1 + (int) (log(_MaxN) / log(2.0)));
d = new Node[n << 1];
for (int i = 1; i <= n + n - 1; i++)
d[i] = Node(inf, i - n + 1);
for (int i = 1; i <= n + n - 1; i++)
d[i] = Node(inf, i >= n ? i - n + 1 : 0);
}
~Heap() {
delete[] d;
}
inline int top_pos() {
return d[1].id;
}
inline void modify(int pos, int s) {
int p = pos + n - 1;
d[p].v = s;
while (p) {
p >>= 1,
d[p] = min(d[(p << 1) + 1], d[p << 1]);
}
}
};
} // Heap
namespace {
const int MAXIN = 1 << 22;
char IN[MAXIN], *SS = IN, *TT = IN;
#ifdef Online
#define gc() (SS == TT && (TT = (SS = IN) + fread(IN, 1, MAXIN, stdin), SS == TT) ? EOF : *SS++)
#else
#define gc() getchar()
#endif
inline int read() {
int now = 0; register char c = gc();
for (; !isdigit(c); c = gc());
for (; isdigit(c); now = now * 10 + c - '0', c = gc());
return now;
}
} // Read
namespace {
struct Edge {
int v, c; Edge* nxt;
Edge() : nxt(nullptr) {}
Edge(int pos, int __, Edge* ___) : v(pos), c(__), nxt(___) {}
} pool[1000005];
int cnt;
#define new_Edge(u, v, c) (pool[cnt] = Edge(u, v, c), &pool[cnt++])
} // Edge
class Graph {
public:
int n;
Edge* head[N];
Graph() {}
~Graph() {
}
inline void AddEdge(int u, int v, int c) {
head[u] = new_Edge(v, c, head[u]);
}
};
class SolveZeroLoop : public Graph {
int du[N];
public:
inline void AddEdge(int u, int v, int c) {
head[u] = new_Edge(v, c, head[u]);
du[v] += 1;
}
SolveZeroLoop(int _) {
n = _;
for (int i = 0; i <= n; i += 1) head[i] = nullptr;
for (int i = 0; i <= n; i += 1) du[i] = 0;
}
~SolveZeroLoop() {
}
unique_ptr<int> topsort(const int* d1, const int* dn, const int& k) {
int* array(new int[n + 1]);
queue<int> que;
int t = 0;
for (int i = 1; i <= n; i += 1)
if (not du[i]) que.push(i), array[i] = t++;
while (not que.empty()) {
int u = que.front(); que.pop();
for (auto edge = head[u]; edge; edge = edge->nxt) {
if (not --du[edge->v]) que.push(edge->v), array[edge->v] = t++;
}
}
for (int i = 1; i <= n; i += 1)
if (du[i] and d1[i] + dn[i] <= k + d1[n]) return nullptr;
return unique_ptr<int>(array);
}
};
class Solution : public Graph {
int f[N][51];
Pair_pro F[N];
public:
Solution(int _) {
n = _;
for (int i = 0; i <= n; i += 1) head[i] = nullptr;
}
~Solution() {
}
void dijkstra(int s, int* dis) {
unique_ptr<Heap> T(new Heap(n + 1));
for (int i = 2; i <= n; i += 1) dis[i] = inf;
dis[s] = 0, T->modify(s, 0);
for (int i = 1; i <= n; i += 1) {
int u = T->top_pos();
T->modify(u, inf);
for (auto edge = head[u]; edge; edge = edge->nxt) {
int v = edge->v;
if (dis[v] > dis[u] + edge->c)
dis[v] = dis[u] + edge->c,
T->modify(v, dis[u] + edge->c);
}
}
}
int Solve(const int k, const int mod, SolveZeroLoop* oG) {
int *d1 = new int[n + 1], *d2 = new int[n + 1];
dijkstra(1, d1), dijkstra(n, d2);
const unique_ptr<int> top_tmp = oG->topsort(d1, d2, k);
int *top = top_tmp.get();
if (top == nullptr) return -1;
for (int i = 1; i <= n; i += 1)
F[i] = Pair_pro(d1[i], top[i], i);
memset(f, false, sizeof f);
sort(F + 1, F + n + 1);
f[1][0] = 1;
for (int j = 0; j <= k; j += 1) {
for (int i = 1; i <= n; i += 1) {
int u = F[i].id;
if (not f[u][j]) continue;
for (auto edge = head[u]; edge; edge = edge->nxt) {
int v = edge->v, ly = d1[u] + j + edge->c - d1[v];
if (ly <= k) f[v][ly] = (f[v][ly] + f[u][j]) % mod;
}
}
}
int res = 0;
for (int i = 0; i <= k; i += 1)
res = (res + f[n][i]) % mod;
return res;
}
};
int main () {
int T = read();
while (T--) {
int n, m, k, p;
n = read(), m = read(), k = read(), p = read();
unique_ptr<Solution> G(new Solution(n));
unique_ptr<SolveZeroLoop> oG(new SolveZeroLoop(n));
for (int i = 0, u, v, c; i < m; i += 1) {
u = read(), v = read(), c = read();
G->AddEdge(u, v, c);
if (not c) oG->AddEdge(u, v, c);
}
printf("%d\n", G->Solve(k, p, oG.get()));
}
return 0;
}
Solution2:
上面那样直接递推答案有点麻烦, 直接记忆化搜索应该是个更好的选择.
可以建出反图来,求出n到所有点的最短路.
设\(f(u,j)\)表示\(u\)到终点的所有路径中, 与最短路为\(j\)的有多少条.
设\(u\rightarrow v\)是正图(非反图)中的一条边, 边权为\(c\), 那么
判断环只需要发现在搜索\(f(u, j)\)的时候又搜索到了自身, 说明有0环.
Code
// luogu-judger-enable-o2
#include <math.h>
#include <queue>
#include <memory>
#include <stdio.h>
#include <string.h>
#include <iostream>
#include <algorithm>
const int inf = 0x3f3f3f3f;
const int N = 100005;
using namespace std;
struct Pair {
int dis, id;
Pair() {}
Pair(int pos, int __) : dis(pos), id(__) {}
bool operator < (const Pair& o) const {
return dis > o.dis;
}
};
#define Online
namespace {
struct Node {
int v; int id;
Node() { }
Node(int _value): v(_value) {}
Node(int _, int __) : v(_), id(__) {}
bool operator < (const Node& o) const {
return v < o.v;
}
};
class Heap {
private:
Node *d; int n;
public:
Heap(int _MaxN) {
n = 1 << (1 + (int) (log(_MaxN) / log(2.0)));
d = new Node[n << 1];
for (int i = 1; i <= n + n - 1; i++)
d[i] = Node(inf, i - n + 1);
for (int i = 1; i <= n + n - 1; i++)
d[i] = Node(inf, i >= n ? i - n + 1 : 0);
}
~Heap() {
delete[] d;
}
inline int top_pos() {
return d[1].id;
}
inline void modify(int pos, int s) {
int p = pos + n - 1;
d[p].v = s;
while (p) {
p >>= 1,
d[p] = min(d[(p << 1) + 1], d[p << 1]);
}
}
};
} // Heap
namespace {
const int MAXIN = 1 << 22;
char IN[MAXIN], *SS = IN, *TT = IN;
#ifdef Online
#define gc() (SS == TT && (TT = (SS = IN) + fread(IN, 1, MAXIN, stdin), SS == TT) ? EOF : *SS++)
#else
#define gc() getchar()
#endif
inline int read() {
int now = 0; register char c = gc();
for (; !isdigit(c); c = gc());
for (; isdigit(c); now = now * 10 + c - '0', c = gc());
return now;
}
} // Read
namespace {
struct Edge {
int v, c; Edge* nxt;
Edge() : nxt(nullptr) {}
Edge(int pos, int __, Edge* ___) : v(pos), c(__), nxt(___) {}
} pool[2000005];
int cnt;
#define new_Edge(u, v, c) (pool[cnt] = Edge(u, v, c), &pool[cnt++])
} // Edge
class Graph {
public:
int n;
Edge* head[N];
Graph(int _) {
n = _;
for (int i = 0; i <= n; i += 1) head[i] = nullptr;
}
inline void AddEdge(int u, int v, int c) {
head[u] = new_Edge(v, c, head[u]);
}
unique_ptr<int> dijkstra(int s) {
unique_ptr<Heap> T(new Heap(n + 1));
int* dis = new int[n + 1];
for (int i = 1; i <= n; i += 1) dis[i] = inf;
dis[s] = 0, T->modify(s, 0);
for (int i = 1; i <= n; i += 1) {
int u = T->top_pos();
T->modify(u, inf);
for (auto edge = head[u]; edge; edge = edge->nxt) {
int v = edge->v;
if (dis[v] > dis[u] + edge->c)
dis[v] = dis[u] + edge->c,
T->modify(v, dis[u] + edge->c);
}
}
return unique_ptr<int> (dis);
}
};
class Solution {
unique_ptr<Graph> G, rG;
int f[N][51], n;
bool instack[N][51];
public:
Solution(int _) : n(_), G(new Graph(_)), rG(new Graph(_)) { }
inline void AddEdge(int u, int v, int c) {
G->AddEdge(u, v, c), rG->AddEdge(v, u, c);
}
int get(int u, const int j, const int* dis, const int& mod) {
if (instack[u][j]) return -1;
if (f[u][j]) return f[u][j];
f[u][j] = (u == n);
instack[u][j] = true;
int tmp, temp;
for (auto edge = G->head[u]; edge; edge = edge->nxt) {
if ((temp = - dis[u] + dis[edge->v] + edge->c) > j) continue;
if ((tmp = get(edge->v, j - temp, dis, mod)) == -1) return -1;
f[u][j] = (f[u][j] + tmp) % mod;
}
return instack[u][j] = false, f[u][j];
}
int Solve(const int k, const int mod) {
memset(f, false, sizeof f);
memset(instack, false, sizeof instack);
unique_ptr<int> dis = rG->dijkstra(n);
return get(1, k, dis.get(), mod);
}
};
int main () {
int T = read();
while (T--) {
int n, m, k, p;
n = read(), m = read(), k = read(), p = read();
unique_ptr<Solution> Sol(new Solution(n));
for (int i = 0, u, v, c; i < m; i += 1) {
u = read(), v = read(), c = read();
Sol->AddEdge(u, v, c);
}
printf("%d\n", Sol->Solve(k, p));
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号