WY模拟赛3
模拟赛3
似乎是学长套题
T1 王浩的复合问题
题目背景
王浩没有谈恋爱,所以并不存在分手和复合,这里的复合问题不是你们期待的那样。
题目描述
王浩在很早以前就学习了\(fibnacci\)数列,即\(f(1)=1,f(2)=1,f(n)=f(n-1)+f(n-2),\)对于求\(n≤10^3\)的项的值是多少的问题,王浩可以用高精度加法很容易地算出来,之前王浩学了矩阵快速幂,代码功力更是大增,对于求\(n≤10^9\),并对第\(n\)项对\(p\)取模的问题可以快速做出来。王浩以前还学过求一个数的数码之和,比如\(233\)的数码之和为\(2+3+3=8\),记为\(g(233)=8\),现在王浩遇到了一个复合问题,就是求\(\sum_{i=1}^n{g(f(i))} mod 9\),请大家帮王浩算出答案是多少
输入格式
第一行是一个整数\(T\),代表有\(T\)组测试数据,接下来有\(T\)行,每行有一个整数\(n\),求复合函数对\(9\)取余数的结果是多少.
输出格式
对于每组数据输出\(T\)行,每行一个整数表示答案。
输入输出样例 #1
输入 #1
1
7
输出 #1
6
说明/提示
【样例解释】
对于第一组询问,\(n=7\),答案为:
【数据范围】
- \(对于10\%的数据 T=1,\ n\le 10\);
- \(对于30\%的数据 T=10^2,\ n\le 10^3\);
对于 \(100\%\) 的数据,满足 \(1\le T\le 10^5,\ 1\le n\le 10^6\)。
赛场思路
通过列举前面几项,可以发现第 $ i $ 个位置的值可以由 $ i-1 $ 和 $ i-2 $ 位相加得到,如果发现和大于 $ 9 $ ,则将数值减去 $ 9 $ 即可,多次询问预处理一下就行。(在比赛时脑子抽了写成大于 $ 10 $ 了)
复杂度 $ O(1e6+T) $ 。
code
#ifdef ONLINE_JUDGE
#else
#define Qiu_Cheng
#endif
#include <bits/stdc++.h>
#define i8 __int128
#define int long long
#define fuck inline
#define lb long double
using namespace std;
// typedef longlong ll;
const int N=1e6+5,M=1e6+520,mod=1e9+7;
const int inf=INT_MAX,INF=1e9+7;
// const int mod1=469762049,mod2=998244353,mod3=1004535809;
// const int G=3,Gi=332748118;
// const int M=mod1*mod2;
fuck int read()
{
int x=0,f=1;
char c=getchar();
while(c<'0'||c>'9'){if(c=='-'){f=-1;}c=getchar();}
while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c-'0');c=getchar();}
return x*f;
}
fuck void write(int x)
{
if(x<0){putchar('-');x=-x;}
if(x>9) write(x/10);
putchar(x%10+'0');
}
int a[N+5],n,ans[N+5];
fuck void pre()
{
a[1]=1,a[2]=1;
for(int i=3;i<=1e6;i++)
{
a[i]=a[i-1]+a[i-2];
if(a[i]>=10) a[i]=a[i]-9;
}
// for(int i=1;i<=100;i++)cout<<a[i]<<"\n";
for(int i=1;i<=N;i++)ans[i]=(ans[i-1]+a[i])%9;
}
fuck void solve()
{
cin>>n;
cout<<ans[n]%9<<"\n";
}
signed main()
{
#ifdef Qiu_Cheng
freopen("1.in","r",stdin);
freopen("1.out","w",stdout);
#endif
// ios::sync_with_stdio(false);
// cin.tie(0); cout.tie(0);
// int fuckccf=read();
// for(int i=1;i<=tot;i++)cout<<prime[i]<<"\n";
pre();
int QwQ=read();
while(QwQ--)solve();
// solve();
return 0;
}
题解思路
题目要求计算 \(\sum_{i=1}^n{g(f(i))} \pmod 9\),其中 \(f(i)\) 是斐波那契数列的第 \(i\) 项 (\(f(1)=1, f(2)=1, f(n)=f(n-1)+f(n-2)\)),\(g(x)\) 是 \(x\) 的数码之和。
关键性质:一个正整数 \(x\) 和它的数码之和 \(g(x)\) 在模 \(9\) 的意义下是同余的。也就是说,\(g(x) \pmod 9 = x \pmod 9\)。
证明:任何一个正整数 \(x\) 可以表示为 \(d_k 10^k + d_{k-1} 10^{k-1} + \dots + d_1 10^1 + d_0 10^0\)。
\(g(x) = d_k + d_{k-1} + \dots + d_0\)。
因为 \(10 \equiv 1 \pmod 9\),所以 \(10^j \equiv 1^j \equiv 1 \pmod 9\) 对任意非负整数 \(j\) 成立。
所以 \(x \pmod 9 = (d_k 10^k + \dots + d_0 10^0) \pmod 9\)
\(= (d_k \cdot 1 + \dots + d_0 \cdot 1) \pmod 9\)
\(= (d_k + \dots + d_0) \pmod 9 = g(x) \pmod 9\)。
利用这个性质,原问题转化为计算 \(\left( \sum_{i=1}^n (f(i) \pmod 9) \right) \pmod 9\)。
接下来我们考虑斐波那契数列模 \(9\) 的性质。数列 \(f(i) \pmod m\) 是周期性的,这个周期称为皮萨诺周期 (Pisano Period)。对于 \(m=9\),皮萨诺周期长度为 \(24\)。
\(f(i) \pmod 9\) 的序列如下:
\(1, 1, 2, 3, 5, 8, 4, 3, 7, 1, 8, 0, 8, 8, 7, 6, 4, 1, 5, 6, 2, 8, 1, 0\)
这个序列长度为 \(24\)。之后序列会重复。
令 \(a_i = f(i) \pmod 9\)。我们要求的是 \(\left( \sum_{i=1}^n a_i \right) \pmod 9\)。
计算一个周期内各项 \(a_i\) 的和:
\(1+1+2+3+5+8+4+3+7+1+8+0+8+8+7+6+4+1+5+6+2+8+1+0 = 99\)。
\(99 \pmod 9 = 0\)。这意味着每 \(24\) 项 \(a_i\) 的和模 \(9\) 为 \(0\)。
设 \(S_k = \left( \sum_{i=1}^k a_i \right) \pmod 9\)。
由于一个完整周期的和模 \(9\) 为 \(0\),我们只需要考虑 \(n\) 除以 \(24\) 的余数部分。
具体来说,\(\left( \sum_{i=1}^n a_i \right) \pmod 9 = S_{n'} \pmod 9\),其中 \(n'\) 是 \(n\) 在周期意义下的等效项数。
如果 \(n \% 24 \ne 0\),则 \(n' = n \% 24\)。
如果 \(n \% 24 = 0\) (即 \(n\) 是 \(24\) 的倍数),则 \(n' = 24\) (表示取完整周期的和)。
这可以统一表示为 \(n' = (n-1) \% 24 + 1\)。这个 \(n'\) 的范围是 \(1\) 到 \(24\)。
我们可以预计算出 \(S_k\) 的值,即 \(P[k] = \left( \sum_{j=1}^k (f(j) \pmod 9) \right) \pmod 9\) 对于 \(k=1, \dots, 24\)。
\(P[1] = (f(1) \pmod 9) \pmod 9 = 1 \pmod 9 = 1\)
\(P[2] = (f(1) \pmod 9 + f(2) \pmod 9) \pmod 9 = (1+1) \pmod 9 = 2\)
...
\(P[24] = (\sum_{j=1}^{24} (f(j) \pmod 9)) \pmod 9 = 99 \pmod 9 = 0\).
预计算的 \(P\) 数组 (1-indexed):
\(P = [1, 2, 4, 7, 3, 2, 6, 0, 7, 8, 7, 7, 6, 5, 3, 0, 4, 5, 1, 7, 0, 8, 0, 0]\)
对于每个查询 \(n\),答案就是 \(P[(n-1)\%24 + 1]\)。
算法步骤:
- 预计算斐波那契数列模 \(9\) 的前 \(24\) 项:\(f_1'=f(1)\pmod 9, f_2'=f(2)\pmod 9, \dots, f_{24}'=f(24)\pmod 9\)。
- 预计算这些项的模 \(9\) 前缀和:\(P[k] = (P[k-1] + f_k') \pmod 9\) (其中 \(P[0]=0\))。这样 \(P[k]\) 存储了 \(\left(\sum_{j=1}^k f_j'\right) \pmod 9\)。
- 对于每个输入的 \(n\),计算 \(idx = (n-1)\%24 + 1\)。
- 输出 \(P[idx]\)。
时间复杂度:预计算 \(O(24)\)。每个查询 \(O(1)\)。总时间复杂度 \(O(24+T) = O(T)\)。
空间复杂度:\(O(24)\)。
好家伙,观察大法起飞了。
T2 王浩的MM
题目描述
王浩的MM中的MM并不是指"美眉","妹妹",也不是长度单位"毫米",以及降雨量单位"毫米"。
王浩的MM是指一个平面被n个字母'm'最多可以分割成多少个平面。
对于1个'm',可以分割成2个平面。
对于2个'm',可以分割成19个平面。
对于给定的n,求王浩的MM是多少。
输入格式
一个整数n,代表有n个字母'M'分割平面.
输出格式
输出最多可以分割的平面数。
输入输出样例 #1
输入 #1
1
输出 #1
2
输入输出样例 #2
输入 #2
2
输出 #2
19
输入输出样例 #3
输入 #3
3
输出 #3
52
说明/提示
【数据范围】
- \(对于10\%的数据 \ n\le 10\);
- \(对于30\%的数据 \ n\le 10^3\);
对于 \(100\%\) 的数据,满足 \(\ 1\le n\le 10^6\)。
赛场思路
通过观察规律大法,以及连蒙带猜,不难得到 $ f(i)-f(i-1)=16 \times i - 15 $ ,于是递推预处理解决问题。
复杂度 $ O(1e6+1) $ 。
code
#ifdef ONLINE_JUDGE
#else
#define Qiu_Cheng
#endif
#include <bits/stdc++.h>
#define i8 __int128
#define int long long
#define fuck inline
#define lb long double
using namespace std;
// typedef longlong ll;
const int N=1e6+5,M=1e6+520,mod=1e9+7;
const int inf=INT_MAX,INF=1e9+7;
// const int mod1=469762049,mod2=998244353,mod3=1004535809;
// const int G=3,Gi=332748118;
// const int M=mod1*mod2;
fuck int read()
{
int x=0,f=1;
char c=getchar();
while(c<'0'||c>'9'){if(c=='-'){f=-1;}c=getchar();}
while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c-'0');c=getchar();}
return x*f;
}
fuck void write(int x)
{
if(x<0){putchar('-');x=-x;}
if(x>9) write(x/10);
putchar(x%10+'0');
}
int ans[N];
fuck void pre()
{
ans[1]=2;
for(int i=2;i<=N;i++)ans[i]=(ans[i-1]+16*i-15);
}
fuck void solve()
{
int n;cin>>n;
cout<<ans[n]<<"\n";
}
signed main()
{
#ifdef Qiu_Cheng
freopen("1.in","r",stdin);
freopen("1.out","w",stdout);
#endif
// ios::sync_with_stdio(false);
// cin.tie(0); cout.tie(0);
// int fuckccf=read();
// for(int i=1;i<=tot;i++)cout<<prime[i]<<"\n";
// int QwQ=read();
// while(QwQ--)solve();
pre();
solve();
return 0;
}
// 6666 66666 666666
// 6 6 6 6 6
// 6 6 6666 6
// 6 6 6 6 6
// 6666 6 6 6666666
题解思路
这是一个平面分割问题。我们要找出 \(n\) 个字母 'm' 最多可以将平面分割成多少部分。
设 \(f(n)\) 为 \(n\) 个 'm' 最多能分割出的平面区域数。
题目给出:
- \(f(1) = 2\):1 个 'm' 可以分割成 2 个平面。
- \(f(2) = 19\):2 个 'm' 可以分割成 19 个平面。
- \(f(3) = 52\) (样例):3 个 'm' 可以分割成 52 个平面。
我们考虑当在已经有 \(n-1\) 个 'm' 的平面上增加第 \(n\) 个 'm' 时,会增加多少区域。
一般地,当向平面上添加一个新的连通的、不自交的曲线(或由线段组成的路径)时,如果它与已有的图形产生 \(k\) 个交点,那么这条新曲线会被分割成 \(k+1\)段。每一段都会将一个已有的区域一分为二,从而增加一个区域。所以,新增的区域数是 \(k+1\)。
假设一个字母 'm' 由 \(S\) 条线段(或基本曲线单元)组成。
当添加第 \(n\) 个 'm'(记为 \(M_n\))时,它会与前面已经存在的 \(n-1\) 个 'm'(\(M_1, \dots, M_{n-1}\))相交。
为了使得分割的区域数最多,我们需要让 \(M_n\) 与 \(M_1, \dots, M_{n-1}\) 的交点尽可能多,并且所有交点都是不同的,不与 'm' 的顶点重合。
\(M_1, \dots, M_{n-1}\) 共有 \(S \times (n-1)\) 条线段。
\(M_n\) 自身有 \(S\) 条线段。\(M_n\) 的每一条线段都可以与前面 \(S \times (n-1)\) 条线段都相交。
所以,\(M_n\) 与 \(M_1, \dots, M_{n-1}\) 之间的总交点数 \(k = S \times (S \times (n-1)) = S^2(n-1)\)。
由于 'm' 是一个连通的形状(例如 /\/\),它增加的区域数是 \(k+1 = S^2(n-1)+1\)。
因此,我们得到递推关系:
\(f(n) = f(n-1) + S^2(n-1) + 1\),对于 \(n > 1\)。
我们可以用 \(f(1)\) 和 \(f(2)\) 的值来确定 \(S\):
\(f(2) = f(1) + S^2(2-1) + 1\)
\(19 = 2 + S^2 \times 1 + 1\)
\(19 = 3 + S^2\)
\(S^2 = 16\)
\(S = 4\)(\(S\) 代表线段数,应为正值)
这意味着每个 'm' 在这个问题中等效于一个由 4 条线段组成的、自身连通的形状。
将 \(S=4\) 代入递推关系:
\(f(n) = f(n-1) + 16(n-1) + 1\),对于 \(n > 1\)。
现在我们求解这个递推关系得到 \(f(n)\) 的通项公式:
\(f(n) = f(1) + \sum_{i=2}^{n} (16(i-1) + 1)\)
令 \(j = i-1\),则当 \(i\) 从 \(2\) 到 \(n\) 时,\(j\) 从 \(1\) 到 \(n-1\)。
\(f(n) = f(1) + \sum_{j=1}^{n-1} (16j + 1)\)
\(f(n) = 2 + 16 \sum_{j=1}^{n-1} j + \sum_{j=1}^{n-1} 1\)
\(f(n) = 2 + 16 \frac{(n-1)n}{2} + (n-1)\)
\(f(n) = 2 + 8n(n-1) + (n-1)\)
\(f(n) = 2 + 8n^2 - 8n + n - 1\)
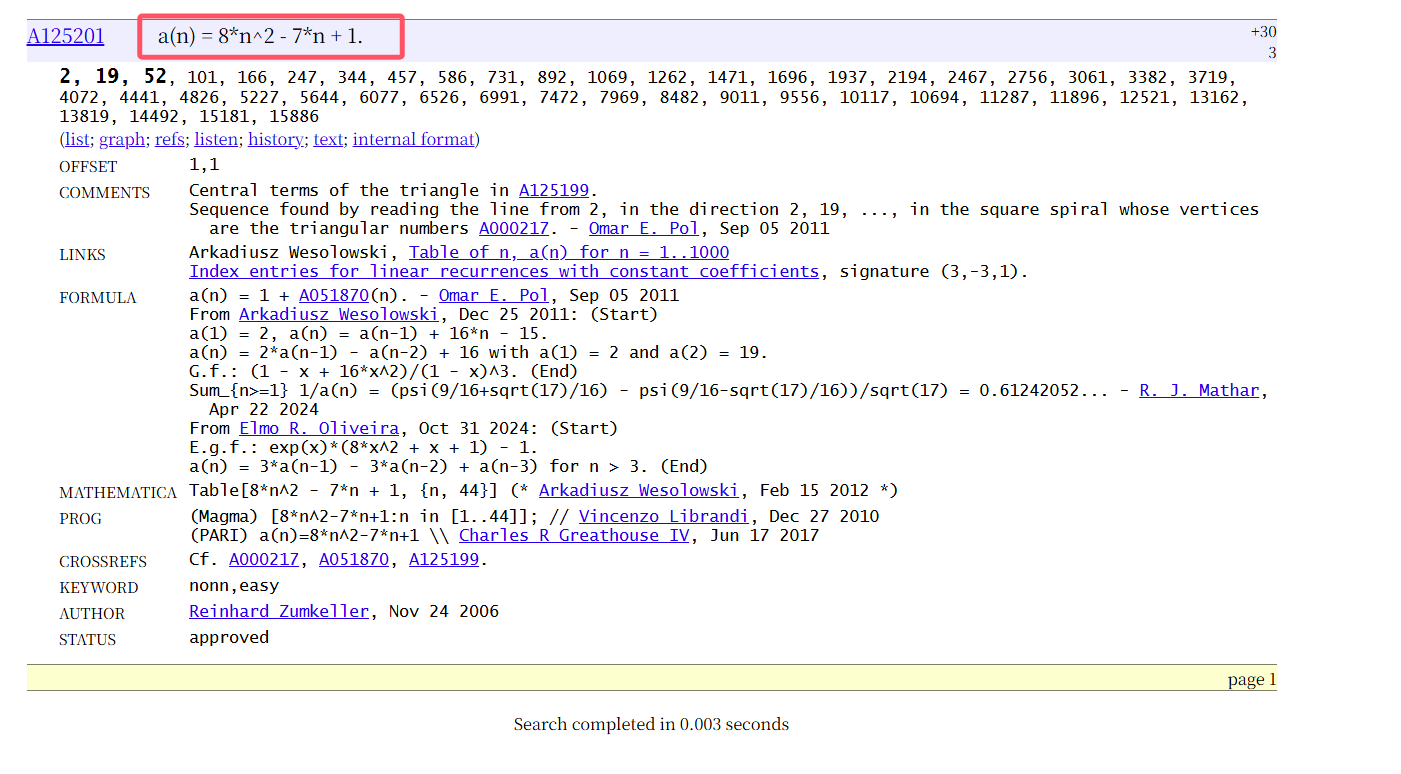
\(f(n) = 8n^2 - 7n + 1\)
我们可以验证这个公式:
- \(n=1: f(1) = 8(1)^2 - 7(1) + 1 = 8 - 7 + 1 = 2\)。正确。
- \(n=2: f(2) = 8(2)^2 - 7(2) + 1 = 8(4) - 14 + 1 = 32 - 14 + 1 = 19\)。正确。
- \(n=3: f(3) = 8(3)^2 - 7(3) + 1 = 8(9) - 21 + 1 = 72 - 21 + 1 = 52\)。正确。
公式 \(f(n) = 8n^2 - 7n + 1\) 是正确的。
由于 \(n\) 的最大值可达 \(10^6\),\(n^2\) 可达 \(10^{12}\)。\(8n^2\) 将是 \(8 \times 10^{12}\) 级别,这个数值需要使用 64 位整型(如 C++ 中的 long long)来存储。
计算时,可以直接使用公式 \(8n^2 - 7n + 1\)。
也可以使用其等价形式,例如 \(n(8n-7)+1\) 或者 \((8n+1)(n-1)+2\)。后者对 \(n=1\) 也成立:\((8(1)+1)(1-1)+2 = 9 \times 0 + 2 = 2\)。
AC 代码
#include <iostream>
int main() {
// 使用 std::ios_base::sync_with_stdio(false) 和 std::cin.tie(NULL)
// 可以加速C++的输入输出流,对于大数据量的输入输出会更有效率。
// 对此题仅读取一个整数,影响不大,但养成习惯有益。
std::ios_base::sync_with_stdio(false);
std::cin.tie(NULL);
long long n; // n 的范围是 1 <= n <= 10^6
std::cin >> n;
// 根据推导出的公式 f(n) = 8n^2 - 7n + 1 计算结果
// 由于 n^2 可能达到 (10^6)^2 = 10^12,结果会非常大,
// 所以必须使用 long long 类型来存储 n 和计算结果。
// 在字面量后加上 LL 后缀(如 8LL)可以确保该字面量是 long long 类型,
// 这有助于保证乘法等运算在提升到 long long 后进行,避免溢出。
long long result = 8LL * n * n - 7LL * n + 1LL;
std::cout << result << std::endl;
return 0;
}
当然你也可以直接用oeis。直接得出通项公式。
3 王浩的233数组
题目描述
王浩坐在CSP-S 2074的赛场上,他已年过古稀,他从CSP-S 2021开始就冲刺提高级一等奖了,可这53年来都未能如愿。他很后悔当初读高中的时候没尽全力跟着吴某人学习,而且跟着王某人一起happy地打游戏,差点把机房的同桌段某人都带入坑了。如今,吴某人已驾鹤西去,代码写着写着就想起了他老人家,想起那机房狼人杀,partner编程,更是潸然泪下,泪流满面的同时,又想起来他老人家临挂之前留下这样一道题。
我们那时候,经常用233表达感情,有时候会用2333,23333,233333都是表达同一种意思。
定义233数组为:
\(a[0][1]=233,a[0][2]=2333,a[0][3]=23333,.......\)
给定递推公式\(a[i][j]=a[i-1][j]+a[i][j-1]\)和\(n,m\)和\(a[1][0],a[2][0],......,a[n][0]\)
求\(a[n][m]\%10000007\).
输入格式
第一行是两个整数\(n\)和\(m\)。
第二行是n个整数分别代表\(a[1][0],a[2][0],......,a[n][0]\)
输出格式
输出一个整数表示答案。
输入输出样例 #1
输入 #1
1 1
1
输出 #1
234
输入输出样例 #2
输入 #2
2 2
666 233
输出 #2
4364
说明/提示
【数据范围】
- \(对于10\%的数据 \ n= 1,m<=10^3\);
- \(对于30\%的数据 n<=5,m<=10^3\);
对于 \(100\%\) 的数据,满足 \(n<=10,m<=10^9,0<a[i][0]<2^{31}\)。
转化的好A
思路
众所周知,取模是不能有除法的,不然会产生小数,导致最后wa了一片。
考虑把除法转化为乘法,也就是将乘 $ x $ 然后除 $ x $ 改为乘 $ 1 $ 。这不是废话吗?不然还真直接除啊? 但是由于每次操作都需要输出,如果用离散化加标记的话仍需要 $ O(nnlog(n)) $ 的复杂度,关于 $ n \leq 1e5 $ ,发现跑得比kiven的乌龟还慢。
联想到似乎可以用线段树维护一下信息,最后输出tree[1]即可,于是就有了一个 $ O(n*log(n)) $ 的做法。
code
#ifdef ONLINE_JUDGE
#else
#define Qiu_Cheng
#endif
#include <bits/stdc++.h>
#define i8 __int128
#define int long long
#define fuck inline
#define lb long double
using namespace std;
// typedef longlong ll;
const int N=1e6+5,M=1e6+520,mod=1e9+7;
const int inf=INT_MAX,INF=1e9+7;
// const int mod1=469762049,mod2=998244353,mod3=1004535809;
// const int G=3,Gi=332748118;
// const int M=mod1*mod2;
fuck int read()
{
int x=0,f=1;
char c=getchar();
while(c<'0'||c>'9'){if(c=='-'){f=-1;}c=getchar();}
while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c-'0');c=getchar();}
return x*f;
}
fuck void write(int x)
{
if(x<0){putchar('-');x=-x;}
if(x>9) write(x/10);
putchar(x%10+'0');
}
int n,p;
int tree[N];
fuck void up(int rt){tree[rt]=(tree[rt<<1]*tree[rt<<1|1])%p;}
fuck void build(int rt,int l,int r)
{
if(l==r&&p!=1){tree[rt]=1;}
else
{
int mid=(l+r)>>1;
build(rt<<1,l,mid);
build(rt<<1|1,mid+1,r);
if(p!=1)up(rt);
}
}
fuck void update(int rt,int l,int r,int pos,int val)
{
int frz=(p==1?0:(val%p));
if(l==r)tree[rt]=frz;
else
{
int mid=(l+r)>>1;
if(pos<=mid)update(rt<<1,l,mid,pos,val);
else update(rt<<1|1,mid+1,r,pos,val);
if(p!=1)up(rt);
}
}
fuck void solve()
{
cin>>n>>p;
build(1,1,n);
for(int i=1;i<=n;i++)
{
int op,x;cin>>op>>x;
if(op==1)update(1,1,n,i,x);
else update(1,1,n,x,1ll);
cout<<tree[1]<<"\n";
}
}
signed main()
{
#ifdef Qiu_Cheng
freopen("1.in","r",stdin);
freopen("1.out","w",stdout);
#endif
// ios::sync_with_stdio(false);
// cin.tie(0); cout.tie(0);
// int fuckccf=read();
// for(int i=1;i<=tot;i++)cout<<prime[i]<<"\n";
// int QwQ=read();
// while(QwQ--)solve();
solve();
return 0;
}
// 6666 66666 666666
// 6 6 6 6 6
// 6 6 6666 6
// 6 6 6 6 6
// 6666 6 6 6666666
T4 王浩的233数组
题目描述
王浩坐在CSP-S 2074的赛场上,他已年过古稀,他从CSP-S 2021开始就冲刺提高级一等奖了,可这53年来都未能如愿。他很后悔当初读高中的时候没尽全力跟着吴某人学习,而且跟着王某人一起happy地打游戏,差点把机房的同桌段某人都带入坑了。如今,吴某人已驾鹤西去,代码写着写着就想起了他老人家,想起那机房狼人杀,partner编程,更是潸然泪下,泪流满面的同时,又想起来他老人家临挂之前留下这样一道题。
我们那时候,经常用233表达感情,有时候会用2333,23333,233333都是表达同一种意思。
定义233数组为:
\(a[0][1]=233,a[0][2]=2333,a[0][3]=23333,.......\)
给定递推公式\(a[i][j]=a[i-1][j]+a[i][j-1]\)和\(n,m\)和\(a[1][0],a[2][0],......,a[n][0]\)
求\(a[n][m]\%10000007\).
输入格式
第一行是两个整数\(n\)和\(m\)。
第二行是n个整数分别代表\(a[1][0],a[2][0],......,a[n][0]\)
输出格式
输出一个整数表示答案。
输入输出样例 #1
输入 #1
1 1
1
输出 #1
234
输入输出样例 #2
输入 #2
2 2
666 233
输出 #2
4364
说明/提示
【数据范围】
- \(对于10\%的数据 \ n= 1,m<=10^3\);
- \(对于30\%的数据 n<=5,m<=10^3\);
对于 \(100\%\) 的数据,满足 \(n<=10,m<=10^9,0<a[i][0]<2^{31}\)。
瞧一瞧,看一看。 $ a[i][j]=a[i-1][j]+a[i][j-1]=a[i-2][j]+a[i-1][j-1]+a[i][j-1] \Rightarrow a[i][j]=a[0][j]+ \sum_{k=1}^{i} a[k][j-1] $ 。对于任意的 $ a[i][j] $ ,我们需要知道 $ a[0][j] $ 和 $ a[k][j-1](1 \leq k \leq i) $ 。 目的是求出 $ a[n][m] $ ,由于 $ m $ 的范围很大所以考虑将 $ m $ 的复杂度优化掉,又因为我们有递推的式子(其中 $ a[0][i]=a[0][i-1]*10+3 $ ),于是可以用矩阵快速幂加速这个过程。
原理:对于一个向量 $ S_{k} $ ,存在一个矩阵 $ T $ 可以使得 $ S_{k}=S_{k-1} \times T $ ,那么 $ S_{m}=S_{0} \times T^{m} $ 。
定义状态向量 \(S_k\)(代表第 \(k\) 列计算所需的信息和结果)如下(向量元素从0开始索引):
\(S_k = \begin{pmatrix} a[1][k] \\ a[2][k] \\ \vdots \\ a[n][k] \\ a[0][k+1] \\ 1 \end{pmatrix}\)
这个向量的维度是 \((n+2) \times 1\)。
其中:
- \(S_k[j]\) (对于 \(0 \le j < n\)) 表示 \(a[j+1][k]\)。
- \(S_k[n]\) 表示 \(a[0][k+1]\)(这是计算下一列 \(k+1\) 时将用到的 \(a[0][\cdot]\) 值)。
- \(S_k[n+1]\) 表示常数 \(1\)。
相应地,\(S_{k-1}\)(代表第 \(k-1\) 列计算所需的信息和结果)为:
\(S_{k-1} = \begin{pmatrix} a[1][k-1] \\ a[2][k-1] \\ \vdots \\ a[n][k-1] \\ a[0][k] \\ 1 \end{pmatrix}\) 。
接下来只需要构建一个 $ (n+2) \times (n+2) $ 的矩阵 $ T $ ,使得 $ S_{m}=S_{0} \times T^{m} $ 。
最终答案 $ a[n][m] $ 即为 $ S[n] $ 。
code
#ifdef ONLINE_JUDGE
#else
#define Qiu_Cheng
#endif
#include <bits/stdc++.h>
#define i8 __int128
#define int long long
#define fuck inline
#define lb long double
using namespace std;
// typedef longlong ll;
const int N=1e6+5,M=1e6+520,mod=1e7+7;
const int inf=INT_MAX,INF=1e9+7;
// const int mod1=469762049,mod2=998244353,mod3=1004535809;
// const int G=3,Gi=332748118;
// const int M=mod1*mod2;
fuck int read()
{
int x=0,f=1;
char c=getchar();
while(c<'0'||c>'9'){if(c=='-'){f=-1;}c=getchar();}
while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c-'0');c=getchar();}
return x*f;
}
fuck void write(int x)
{
if(x<0){putchar('-');x=-x;}
if(x>9) write(x/10);
putchar(x%10+'0');
}
int n,m;
int s[15],t[15][15],c[15][15],a[15];
fuck void clr()
{
for(int i=1;i<=n+2;i++)
for(int j=1;j<=n+2;j++)a[i]=c[i][j]=0;
}
fuck void jc1()
{
clr();
for(int i=1;i<=n+2;i++)
for(int j=1;j<=n+2;j++)
a[i]=(a[i]+s[j]*t[j][i])%mod;
for(int i=1;i<=n+2;i++)s[i]=a[i];
}
fuck void jc2()
{
clr();
for(int i=1;i<=n+2;i++)
for(int j=1;j<=n+2;j++)
for(int k=1;k<=n+2;k++)c[i][j]=(c[i][j]+t[i][k]*t[k][j])%mod;
for(int i=1;i<=n+2;i++)
for(int j=1;j<=n+2;j++)t[i][j]=c[i][j];
}
fuck void solve()
{
cin>>n>>m;
for(int i=1;i<=n;i++)cin>>s[i];s[n+1]=233,s[n+2]=1;
for(int i=1;i<=n+2;i++)
for(int j=1;j<=n+2;j++)t[i][j]=0;
for(int j=1;j<=n;j++)
for(int i=1;i<=1+j;i++)t[i][j]=1;
t[n+1][n+1]=10;t[n+2][n+1]=3;t[n+2][n+2]=1;
while(m)
{
if(m&1)jc1();
jc2();
m>>=1;
}
cout<<s[n]%mod<<"\n";
}
signed main()
{
#ifdef Qiu_Cheng
freopen("1.in","r",stdin);
freopen("1.out","w",stdout);
#endif
// ios::sync_with_stdio(false);
// cin.tie(0); cout.tie(0);
// int fuckccf=read();
// for(int i=1;i<=tot;i++)cout<<prime[i]<<"\n";
// int QwQ=read();
// while(QwQ--)solve();
solve();
return 0;
}
// 6666 66666 666666
// 6 6 6 6 6
// 6 6 6666 6
// 6 6 6 6 6
// 6666 6 6 6666666
完结收工!!!!!

看完点赞,养成习惯
\(\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号