树与图计数

观前提示：本文并不含任何多项式内容。

本文疑似要成科普文章了。

图计数

有向有标号有向图数量：\(2^{n \choose 2}\)。后面叫做 \(g(n)\)

证明：显然。

有向有标号连通图数量：设答案叫做 \(f(n)\)

方法一：

考虑容斥，枚举点 \(1\) 所在的连通块大小。

就是 \(f(n)=g(n)-\sum\limits_{i=1}^{n-1} {{n-1} \choose {i-1}} g(i) g(n-i)\)

复杂度 \(O(n^2)\)

方法二： 考虑 GF，嘟嘟嘟。

这个东西好像是 Exp 的组合意义。

P6596

非常好题目，让我容斥旋转。

有向有标号有向图数量：\(2^{n \choose 2}\)。后面叫做 \(g(n)\)

证明：显然。

有向有标号连通图数量：设答案叫做 \(f(n)\)

考虑容斥，枚举点 \(1\) 所在的连通块大小。

就是 \(f(n)=g(n)-\sum\limits_{i=1}^{n-1} {{n-1} \choose {i-1}} g(i) g(n-i)\)

复杂度 \(O(n^2)\)

一个结论：一个 \(n\) 个点 \(m\) 条边的带标号无向图有 \(k\) 个连通块。我们希望添加 \(k-1\) 条边使得整个图连通，求方案数。

答案是 \(n^{k-2} \prod s_{i}\)， 其中 \(s_i\) 是每个连通块的数量。

证明见OI-wiki。

意思就是说：我们只是关心后面的那一坨。考虑 dp，设 \(H_{i,j}\) 表示有 \(i\) 个点，\(j\) 条割边，后面的东西的乘积。还是要考虑枚举连通块 \(H_{i,j}=\sum\limits_{k=1}^{i-1} H_{i-k,j-1} \times H_{k,0}\)。 注意下这里因为我们没有钦定边双的顺序，最后的时候要除以一个\((j+1)!\)。

那我们的边界条件怎们做啊！！

实际上很简单，只需要用 \(g(n)\) 减去其他的就行了。

此时 \(H_{i,0}= \texttt{边双连通图} \times i\)

紧急加更 LGV 引理

点双连通计数

无向图三元环计数

树计数

Prufer

一棵有标号无根的树与 一个 \(n-2\) 的排列构成双射。

然后就没了。

扩展结论：一个 \(n\) 个点 \(m\) 条边的带标号无向图有 \(k\) 个连通块。我们希望添加 \(k-1\) 条边使得整个图连通，求方案数。

答案是 \(n^{k-2} \prod s_{i}\)， 其中 \(s_i\) 是每个连通块的数量。

Matrix Tree

杨表

写不动题目，只能来看论文了/ll。

速通的。

杨图

每一行（或者是列） 单调递减。

我们用整数分拆的符号 \(\lambda\) 表示 杨图。

下面是一个 \(\lambda =(5,4,1)\) 的杨图。

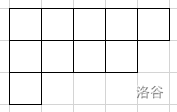
臂长，腿长，钩长

臂长：单元格右边的单元格数，记作 $ a_\lambda(x,y)$。

腿长：单元格下边的单元格数，记作 $ l_\lambda(x,y)$。

钩长：上面两个加起来，加上本身。记作 $ h_\lambda(x,y)$。

显然 \(h_\lambda(x,y)=a_\lambda(x,y)+l_\lambda(x,y)+1\)

杨表

在杨图中填上集合内的元素。一般是数字。

标准杨表是满足每列数字严格递增、每行数字严格递增的杨表。

半标准杨表是满足每列数字严格递增、每行数字非严格递增的杨表。

标准杨表的 RSK 算法

Aim：将一个数 \(k\) 插入一个标准杨表。

• 移动至第一行。
• 遍历，从左往右找到一个 \(> k\) 的数 \(x\)。
• 如果没有，放在最后一个，否则交换两个数。
• 继续执行第二个操作。

正确性显然。

其实并不。

杨表的性质

直接开始贺了，不演了

LIS：最长上升子序列，LDS：最长下降子序列。

将排列\(P_{1},P_{2} \dots P_{n}\)按 RSK 算法依次插入得到杨表 \(S\)，有性质：

• 第一行长度 \(S_1\)为排列的 LIS 长度（内容不一定）。
• 第一列长度为排列的 LDS 长度（内容不一定）。
• 若将排列 \(P_{n},P_{n-1} \dots P_{1}\) 插入杨表 \(S'\)，则 \(S′\) 是 \(S\) 交换行列得到。

感性理解不难。

钩长公式

没有证明哦。

对于一个杨图 \(\lambda\)，填入一个 \(\left[1,n\right]\) 的排列，设 \(D_\lambda\) 表示合法的标准杨表数，我们有：

\[D_{\lambda} = \dfrac{n \texttt{!}}{\prod h_{\lambda}(i,j)} \]

Robinson–Schensted correspondence

和拆分数有映射关系。

实际上，和排列是双射的。

\[\sum\limits_{\lambda \in P_{n}} (D_{\lambda})^2 = n! \]

其中\(P_{n}\) 是和为 \(n\) 的拆分数形成的集合。

注意有一个关键近似 $ |P_{n}| \sim \frac{1}{4\sqrt{3}n} e^{\sqrt{\frac{2n}{3}} \pi}$

抽象。

杨表和LGV引理有一点相同之处。