学号20182317 2019-2020-1 《数据结构与面向对象程序设计》第九周学习总结

学号20182317 2019-2020-1 《数据结构与面向对象程序设计》第九周学习总结

教材学习内容总结

三种常用的查找算法(顺序查查找，折半查找，二叉排序树查找)

树

树的基本性质：
  • 结点：包含了数据项和指向其他结点的分支
  • 结点的度：结点所拥有的子树棵树。
  • 叶结点&终端结点：即度为0的结点
  • 分支结点&非终端结点：除了叶结点以外的其他结点
  • 子女结点：若结点x有子树，则子树的根结点即为结点x的子女。
  • 父结点：若结点x有子女，它即为子女的父结点
  • 根结点：没有父结点的结点称为根结点
  • 兄弟结点：同一父结点的子女互称为兄弟。
  • 树的高度：叶结点的高度为1，非叶结点的高度等于它子女结点高度的最大值加1。该树的高度为4
  • 树的度：树中结点的度的最大值。
树的遍历
  • 前序遍历：从根结点开始，访问每一结点及其孩子。
  • 中序遍历：从根结点开始，访问结点的左孩子，然后是该结点，再然后是任何剩余结点。
  • 后序遍历：从根结点开始，访问结点的孩子，然后是该结点。
  • 层序遍历：从根结点开始，访问每一层的所有结点，一次一层。
  • 中序 + 先序，或 中序 + 后序 均能唯一确定一棵二叉树，但 先序 + 后序 却不一定能唯一确定一棵二叉树。

如上图所示，该树的不同遍历方式依次遍历结点的顺序如下：

    • 先序遍历：A B D E H I K C F G J
    • 中序遍历：D B H E K I A F C G J
    • 后序遍历：D H K I E B F J G C A

  • 二叉树（Binary Tree）

  • 是另外一种树型结构，它的特点是每个节点至多只有两棵子树（即二叉树中不存在度大于2的结点），并且，二叉树的子树有左右之分，其次序不能任意颠倒。

  • 与树的递归定义类似，二叉树的递归定义如下：二叉树或者是一棵空树，或者是一棵由一个根结点和两棵互不相交的分别称为根的左子树和右子树的子树所组成的非空树。

  • 由以上定义可以看出，二叉树中每个结点的孩子数只能是0、1或2个，并且每个孩子都有左右之分。位于左边的孩子称为左孩子，位于右边的孩子称为右孩子；以左孩子为根的子树称为左子树，以右孩子为根的子树称为右子树。

  • 二叉树的构建：


    public List<TreeNode> createTree(){
 
        int[] array = {1,2,3,4,5,6,7,8,9};
 
        List<TreeNode> nodeList = new ArrayList<>();
 
        for (int nodeIndex = 0; nodeIndex < array.length;nodeIndex++){
            nodeList.add(new TreeNode(array[nodeIndex]));
        }

        //对LastParentIndex-1个父节点按照父节点和子节点的关系建立二叉树
        for (int parentIndex = 0; parentIndex < array.length/2-1;parentIndex++){
 
            //左孩子
            nodeList.get(parentIndex).left =  nodeList.get(parentIndex * 2 +1);
            //右孩子
            nodeList.get(parentIndex).right =  nodeList.get(parentIndex * 2 +2);
 
        }
 
        //最后一个父节点，可能存在没有右孩子的情况，所以拿出来单独处理
        int lastParentIndex = array.length/2-1;
 
        //左孩子
        nodeList.get(lastParentIndex).left =  nodeList.get(lastParentIndex * 2 + 1);
 
        //右孩子，如果长度为奇数则建立右孩子
        if(array.length % 2 == 1){
            nodeList.get(lastParentIndex).right = nodeList.get(lastParentIndex * 2 + 2);
        }
 
        return nodeList;
    }

教材学习中的问题和解决过程

  • 问题1：完全二叉树和满二叉树的关系

  • 问题1解决方案：完全二叉树是由满二叉树而引出来的。对于深度为K的，有n个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。

    对于满二叉树，除最后一层无任何子节点外，每一层上的所有结点都有两个子结点二叉树。而完全二叉树是效率很高的数据结构，完全二叉树是由满二叉树而引出来的。 对于深度为K的，有n个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。

  • 问题2：二叉树查找方法相对于其他查找方法的优越性

  • 问题2解决方案：树是一种非线性的数据结构，相对于线性的数据结构(链表、数组)而言，树的平均运行时间更短(往往与树相关的排序时间复杂度都不会高)

代码调试中的问题和解决过程

  • 问题1：教材中的BTNode类和LinkedBinaryTree中的一些代码涉及到ArrayIterator类，无法调用该类。

  • 问题1解决方案：自己编写一个类，使得程序实现

代码托管

（statistics.sh脚本的运行结果截图）

上周考试错题总结

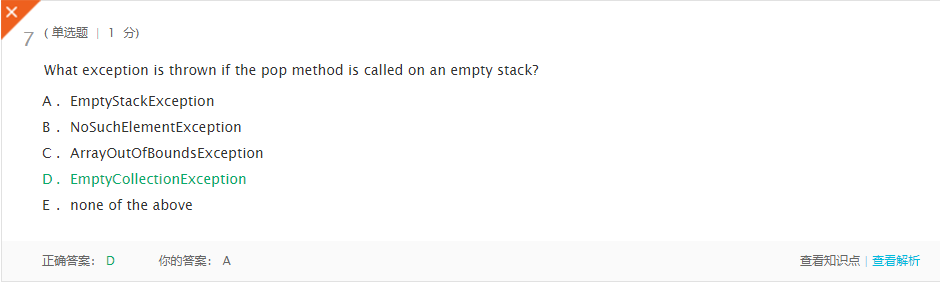
  • 解析：如果在空堆栈上调用pop方法，系统就会抛出错误

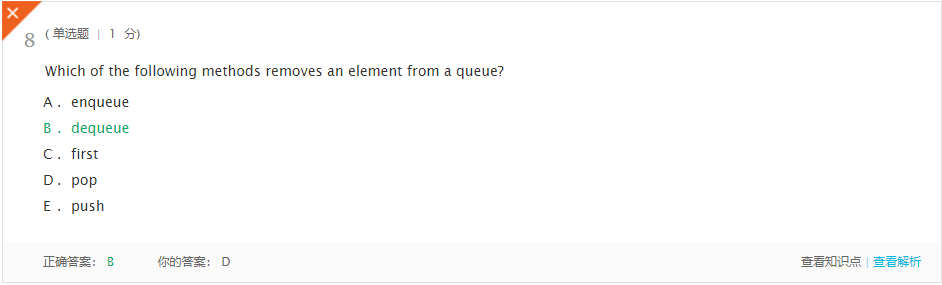
  • 解析：dequeue方法从队列中移除元素

  • 解析：队列是模拟先进先出服务的理想选择

结对及互评

评分标准

  • 基于评分标准，我给本博客打分：14分。得分情况如下：

  1. 正确使用Markdown语法（加1分）：

    • 不使用Markdown不加分

    • 有语法错误的不加分（链接打不开，表格不对，列表不正确...）

    • 排版混乱的不加分

  2. 模板中的要素齐全（加1分）

    • 缺少“教材学习中的问题和解决过程”的不加分
    • 缺少“代码调试中的问题和解决过程”的不加分
    • 代码托管不能打开的不加分
    • 缺少“结对及互评”的不能打开的不加分
    • 缺少“上周考试错题总结”的不能加分
    • 缺少“进度条”的不能加分
    • 缺少“参考资料”的不能加分

  3. 教材学习中的问题和解决过程, 一个问题加1分

  4. 代码调试中的问题和解决过程, 一个问题加1分

  5. 本周有效代码超过300分行的（加2分）

    • 一周提交次数少于20次的不加分

  6. 其他加分：

    • 感想，体会不假大空的加1分
    • 排版精美的加一分
    • 进度条中记录学习时间与改进情况的加1分
    • 有动手写新代码的加1分
    • 课后选择题有验证的加1分
    • 代码Commit Message规范的加1分
    • 错题学习深入的加1分
    • 点评认真，能指出博客和代码中的问题的加1分
    • 结对学习情况真实可信的加1分

点评过的同学博客和代码

  • 本周结对学习情况
    • 20182318
    • 20182333
    • 结对学习内容
      • 对一些程序渐进复杂度的计算
      • 对栈的一些讨论和学习。包括出栈，入栈，删除等等
  • 对队列的一些讨论和学习。包括链表和数组实现队列，入队、出队等等
  • 上周博客互评情况

其他（感悟、思考等，可选）

经过本周的学习,我对曾经学过的知识有了更深一步的了解同时对数据查找和排序等方法的应用也更加熟悉，同时也弄懂了一些过去不是很懂的知识点可谓是受益匪浅。

学习进度条

代码行数（新增/累积） 博客量（新增/累积） 学习时间（新增/累积） 重要成长
目标 5000行 30篇 400小时
第一周 126/126 2/2 20/20
第二周 0/126 2/2 20/40
第三周 353/479 2/6 20/60
第四周 1760/2239 2/8 30/90
第五周 1366/3615 2/10 20/110 
     |

| 第六周 | 534/4149 | 2/12 | 20/130 |
| 第七周 | 2800/6949 | 2/12 | 20/150 | |
| 第八周 | 883/7832 | 2/14 | 20/170 | |
| 第九周 | 2550/10382 | 2/126 | 20/190 |　　

参考资料

posted @ 2019-11-19 13:58  20182317彭衍泰  阅读(177)  评论(0)  编辑  收藏  举报