数据结构之二叉树

树是一种重要的复杂数据结构，常见的数据结构还有数组、链表、栈、队列、散列表、树、图

其中树的分类比较多，而且应用也十分广泛，本文主要介绍二叉树

二叉树作为一种最为典型的树，其重要性不言而喻，其中二叉树又可以大致细分为完全二叉树、满二叉树、平衡二叉树、霍夫曼树、（线索二叉树、红黑树、B树、二叉排序树），本文旨在介绍前面的四种树

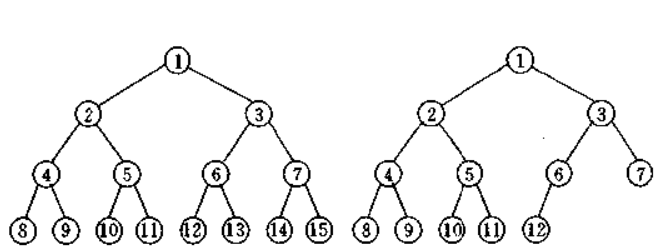
满二叉树(左)跟完全二叉树(右)的区别:二叉树的建立是有规则的，按照从上至下，从左至右的方式建立了两棵二叉树；下左是满二叉树，其特点就是每个节点有且只有两个子节点（最后一层除外），而下右是完全二叉树，从元素对应位置来看，它跟满二叉树的所有元素位置都是一一对应的，只是缺失了一部分，根据建立树的规则，从上到下，从左到右，所以缺失的部分都是在数的右边，也就是右子树。借用百度百科的原话:完全二叉树是效率很高的数据结构，完全二叉树是由满二叉树而引出来的。对于深度为K的，有n个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。

 

 

平衡二叉树:首先平衡二叉树本质上还是一颗二叉查找树，而二叉查找树:对任意节点来说，右子树上的数据>节点上的数据>左子树上的数据，相对于二叉查找树而言，平衡二叉树多了一个特点，那就是平衡二叉树的任意一个节点，它的左右子树的高度差的绝对值不能超过1.

霍夫曼树（别名哈夫曼树、带权路径最小二叉树、最优二叉树）:借用百度百科的原话:给定N个权值作为N个叶子结点，构造一棵二叉树，若该树的带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树，权值较大的结点离根较近。

对于霍夫曼树，重点掌握其构建思路即可，点击此即可了解