几个NPC问题的简单规约

因为一直都不怎么会 NPC 问题的规约证明，于是记录一下今天看到的几个简单的问题。

首先这里的 NPC 问题都是规约到 3-SAT 上的，3-SAT 问题的即有 \(n\) 个 \(01\) 变量 \(x_i\) 和 \(m\) 个限制，每个限制为有一个三元组 \(C_j=(a,b,c)\) 其中 \(a,b,c\in\{x_i,\neg x_i\}\)，对于每一个限制要满足 \(a,b,c\) 不能均为 false。

显然所有的 SAT 问题都可以通过建虚点的形式转化成 3-SAT 问题。然后有一个 ETH 猜想，即不存在能在 \(2^{o(n)}poly(|I|)\) 的复杂度内判定 3-SAT 的算法（\(I\) 指输入）。

Subset Sum

问对于大小为 \(n\) 一个集合 \(S\)，能否从中找到一个子集满足子集中的元素之和为 \(k\)。

对于每个变量我们建立两个元素 \(a_i,b_i\)，其中 \(a_i=10^{i-1}+\sum_{x_i\in C_j} 10^{n+j-1},b_i=10^{i-1}+\sum_{\neg x_i\in C_j} 10^{n+j-1}\) 第 \(i-1\) 相当于表示 \(x_i\) 有没有赋值，然后第 \(n+j-1\) 位则表示 \(C_j\) 有几个变量的值跟要求是一样的。然后再对每个限制增加两个元素 \(c_i=d_i=10^{n+j-1}\) 用于补不满足的（补成一定有 \(3\) 个满足）。

然后令 \(k=\sum_{i=1}^{n} 10^{i-1}+\sum_{j=1}^{m} 3 \cdot 10^{n+j-1}\) 做 Subset Sum 即可。

Knapsack

有 \(n\) 个物品的集合 \(S\)，每个物品有一个重量 \(w_i\) 和权值 \(v_i\)，对于集合 \(T\) 设 \(w(T)=\sum_{i\in T}w_i,v(T)=\sum_{i\in T}v_i\)。给定背包大小 \(C\)，求 \(\max_{w(T)\le C} V(T)\)。

设一个 Subset Sum 问题中的元素为 \(a_i\)，那么令 \(w_i=v_i=a_i,C=k\) 做一遍背包然后检查是否等于 \(k\) 即可。

从这两个规约可以看出，Knapsack 问题不存在 \(2^{o(\sqrt{|I|})}\) 复杂度的做法。（根号的原因是将 3-SAT 问题规约到背包我们的值域是 \(O(10^m)\) 所以输入是 \(O(m^2)\)）。

然后一个 \(2^{O(\sqrt{|I|})}\) 解决 01 背包问题的方法就是，如果 \(n\le O(\sqrt {|I|})\) 就 \(2^n\) 暴力，否则对于权值最大的 \(\sqrt n\) 个暴力，对于剩下的做值域为 \(O(\sqrt{|I|})\) 的背包就好啦。

无向图染色问题

给定一个无向图和 \(k\) 种颜色，判断能否染色使得有边的两个点不同色。

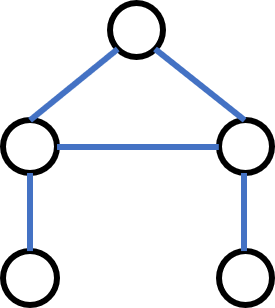
考虑只有 \(3\) 种颜色的时候，可以简单地将或操作通过染色实现，然后就可以规约到 3-SAT 了，具体如下图。（下面两个是输入，上面是输出）