P1668 [USACO04DEC] Cleaning Shifts S

原题链接

题解

题意提醒： 这里的时间段要抽象成点，比如 \([1,1] , [2,2]\) 实际上是相连的！！
1.朴素想法，每头牛要么值班要么不值班， 搜索遍历所有情况 \(O(2^n)\)
2.稍作修改，如果一头牛值班，那么在它值班结束时间之前值班的牛的数量一定是最优的，\(o(nT)\)
3.换个思路，已知要覆盖 \([1,T]\) 这个时间段，所以左端点为 \(1\) 的牛必须选一个，且选右端点最大的那个，设这个最大的右端点为 \(r\) 如果我们把 \(r\) 看成 \(1\) 那么又回到了刚才的情况，只不过这次可以选择的区间左端点变成了小于等于 \(r\)，操作同上，直到 \(r \geq T\)
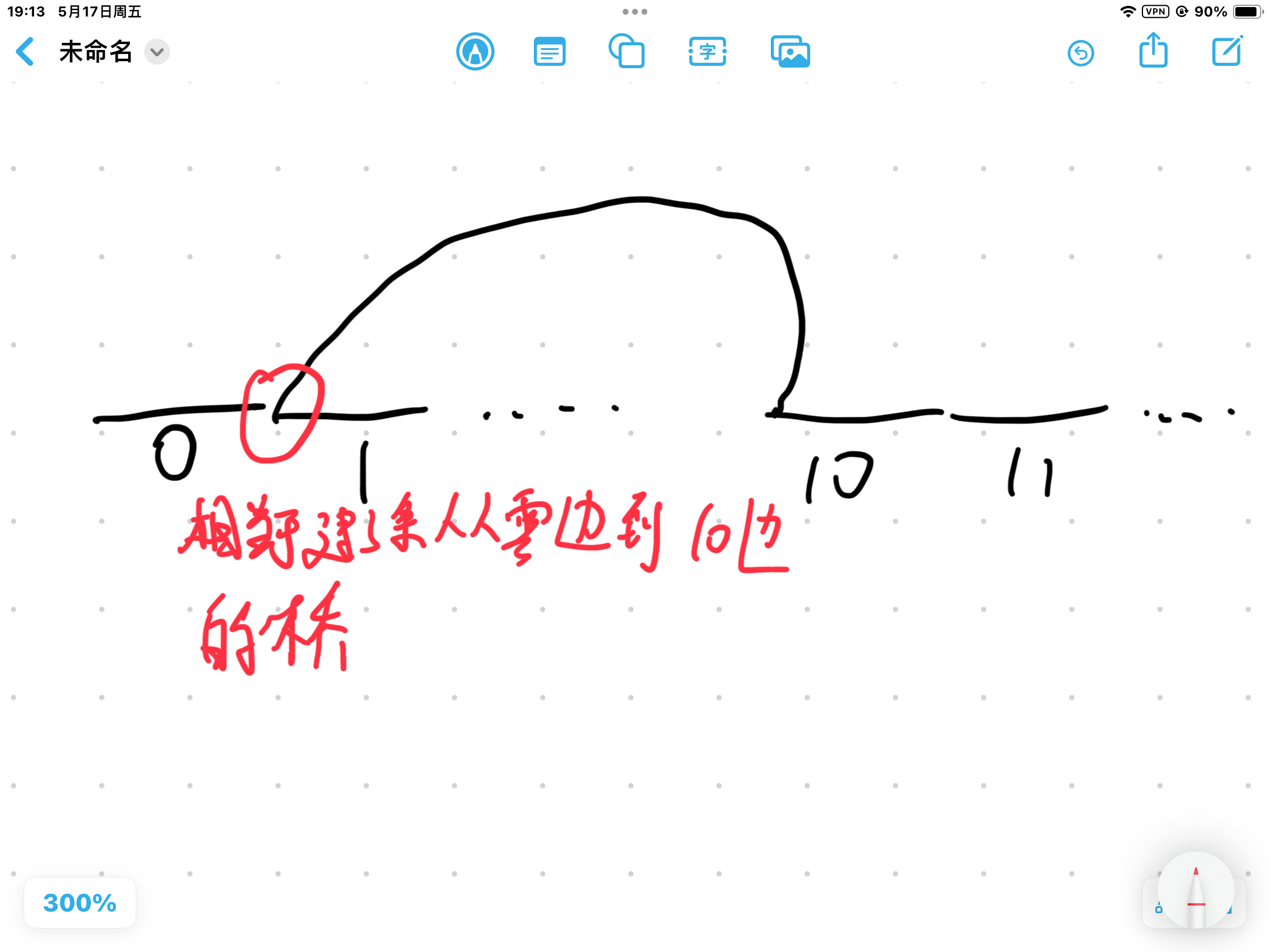
4.再换个思路，我们把区间看成路，时间看成城市，则变成了从城市 \(1\) 到城市 \(T\) 最少要走几条路？由于区间可以重叠，所以我们让编号高的城市可以免费回到编号低的城市
建图的时候变成 \((l-1) \to r,val=1\)
\(i \to (i-1) , val=0\)
从零点出发，最后求 \(dis[T]\)

code1（更优）

#include<bits/stdc++.h>
using namespace std;
const int MAX=2e9;
struct node
{
    int s,e;
}cow[25005];
bool cmp(node a,node b)
{
    return a.s<b.s;
}
int main()
{
    int n,t;
    cin>>n>>t;

    for(int i=1;i<=n;i++) cin>>cow[i].s>>cow[i].e;

    sort(cow+1,cow+1+n,cmp);

    int r=0,it=1,cnt=0;//这里的r代表目前 [1,r] 时间段有值班
    while(r<t&&it<=n)
    {
        int e=r;
        while(it<=n&&cow[it].s-1<=r) e=max(e,cow[it++].e);//执行收获操作的条件要注意！！！
        if(e==r) break;
        cnt++;
        r=e;
        //cout<<r<<endl;
    }
    if(r>=t) cout<<cnt;
    else cout<<-1;
    return 0;
}

code2（巧妙）

#include<bits/stdc++.h>
using namespace std;
const int MAX=2e9;
struct node
{
    int pos,val;
    bool operator<(const node &b)const{return b.val<val;}
};
struct edge
{
    int to,len;
};
vector<edge> G[1000006];//时间看成城市
int dis[1000006];
int main()
{
    memset(dis,0x3f,sizeof dis);
    int n,t;
    cin>>n>>t;
    for(int i=1;i<=n;i++)
    {
        int x,y;
        cin>>x>>y;
        G[x-1].push_back({y,1});
    }

    for(int i=1;i<=t;i++) G[i].push_back({i-1,0});//点看成边，

    priority_queue<node> q;
    q.push({0,0});

    while(q.size())
    {
        int now=q.top().pos,val=q.top().val;

        q.pop();
        if(dis[now]<=val) continue;

        dis[now]=val;
        for(auto next:G[now])
        {
            int to=next.to,len=next.len;
            q.push({to,dis[now]+len});
        }
    }

    if(dis[t]>25000) cout<<-1;
    else cout<<dis[t];
    return 0;
}