彻底搞定排序（一）

排序总结

微信原文

冒泡排序、插入排序、选择排序、归并排序、快速排序、计数排序、基数排序、桶排序。

速查表

类别	方法	复杂度	最好	最坏	空间	稳定性
插入排序	插入排序	\(O(n^2)\)	\(O(n)\)	\(O(n^2)\)	\(O(1)\)	稳定
	希尔排序	\(O(n^{1.3})\)	\(O(n)\)	\(O(n^2)\)	\(O(1)\)	不稳定
选择排序	选择排序	\(O(n^2)\)	\(O(n^2)\)	\(O(n^2)\)	\(O(1)\)	不稳定
	堆排序	\(O(nlog_2n)\)	\(O(nlog_2n)\)	\(O(nlog_2n)\)	\(O(1)\)	不稳定
交换排序	冒泡排序	\(O(n^2)\)	\(O(n)\)	\(O(n^2)\)	\(O(1)\)	稳定
	快速排序	\(O(nlog_2n)\)	\(O(nlog_2n)\)	\(O(n^2)\)	\(O(1)\)	不稳定
归并排序		\(O(nlog_2n)\)	\(O(nlog_2n)\)	\(O(nlog_2n)\)	\(O(n)\)	稳定

两个概念

• 原地排序

  原地排序算法，就是特指空间复杂度是\(O(1)\)的排序算法

• 稳定性

  这个概念是说，如果待排序的序列中存在值相等的元素，经过排序之后，相等元素之间原有的先后顺序不变。

冒泡排序

冒泡排序只会操作相邻的两个数据。每次冒泡操作都会对相邻的两个元素进行比较，看是否满足大小关系要求。如果不满足就让它俩互换。

原地：不涉及辅助空间\(O(1)\)

稳定：相同元素不必交换

复杂度：

• 最好情况（已经有序），需要一次遍历\(O(n)\)
• 最坏情况，需要n次遍历，\(O(n^2)\)

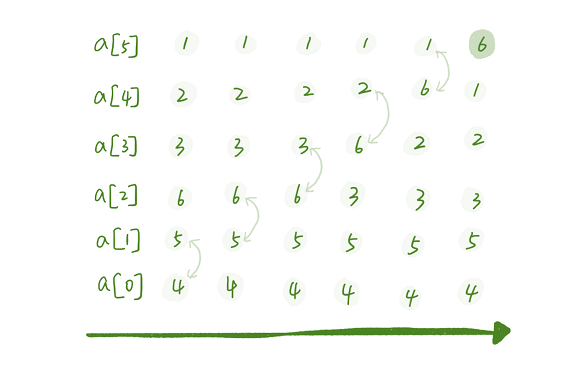
插入排序

数组中的数据分为两个区间，已排序区间和未排序区间。是取未排序区间中的元素，在已排序区间中找到合适的插入位置将其插入，并保证已排序区间数据一直有序。

插入排序也包含两种操作，一种是元素的比较，一种是元素的移动。

原地：不涉及辅助空间\(O(1)\)

稳定：相同元素可以指定顺序，后面出现的放在后面

复杂度：

• 最好情况（已经有序），需要一次遍历\(O(n)\)
• 最坏情况，需要n次遍历，\(O(n^2)\)

选择排序

选择排序算法的实现思路有点类似插入排序，也分已排序区间和未排序区间。但是选择排序每次会从未排序区间中找到最小的元素，将其放到已排序区间的末尾。

原地：不涉及辅助空间\(O(1)\)

稳定：选择排序每次都要找剩余未排序元素中的最小值，并和前面的元素交换位置，这样破坏了稳定性。

复杂度：

• 每次都要选，所以是\(O(n^2)\)

冒泡排序、插入排序、选择排序这三种排序算法，它们的时间复杂度都是 O(n2)，比较高，适合小规模数据的排序。