splay 学习笔记

upd : 之前写的什么垃圾玩意。。。

这里不侧重讲板子，板子没啥好讲的/fn。

考虑 splay 其实就是 BST ，然后 BST 的话树高不保证，于是在 splay 中加上了一个 rotate 和 splay 操作，从而可以让 splay 在旋转保证树高的期望是 \(\log\) 的。

具体的来说就是下面这样的，这里偷盗 @attack 大佬的图片。

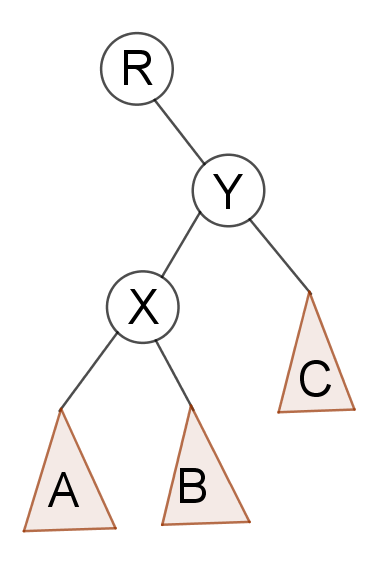
就是说对于一个节点，我们对其操作之后，我们考虑在保证原树满足 BST 性质的前提下，我们将其转到根。

对于上图， \(x\) 本来应该是 \(y\) 的左儿子，然后我们将其往上转。

这个时候发现 \(y\) 变成了 \(x\) 的右儿子，然后对应的 A，B，C 子树也在发生变化。

比如原树中根据二叉树的性质，我们可发现对于权值上的关系肯定是： \(A<X<B<Y<C\)。

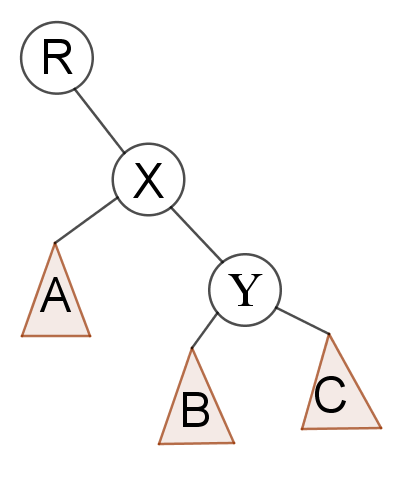
然后你发现，我们因为将 \(x\) 替代了 \(y\) 的位置，那么我们仍要保证二叉树满足这个 BST 性质。

然后我们一个很直接的想法是，对于比 x 大的，分配到他的右子树，比 x 小的，分配到左子树。

然后因为里面只有 A < X， 所以 A 仍然为 X 的左儿子，然后对于 Y， B， C 来说，我们发现可以让 Y 成为 B 和 C 的父亲， B 成为 Y 的左儿子，C 为 Y 的右儿子。

然后你发现这个好像很有规律的，对于前后变换。

那继续考虑手玩右儿子。

然后手玩为右儿子的情况就可以写出旋转的函数：

void rotate(int x) {
  int f = t[x].fa, ff = t[f].fa, c = (rs(f) == x), d = t[x].ch[c ^ 1];
  t[x].fa = ff;  if( ff ) t[ff].ch[rs(ff) == f] = x;
  t[f].fa = x;  t[x].ch[c ^ 1] = f;  t[f].ch[c] = d;  t[d].fa = f;
  pushup(f),  pushup(x);
}

啊，我好敷衍啊.... 确实挺敷衍的，不过就这样吧。

然后 splay 操作就是一直把这个提到根节点的过程中一直 rotate ，然后可以最后通过势能分析证明复杂度为 \(n \log n\) 的。

然后也可以提到某个节点，然后我们 splay 也一般用的是双旋，而非单旋，看代码把（）

void splay(int x,int tar = 0) {
  int u = x;  st[++tp] = x;
  while( t[u].fa != tar) st[++tp] = (u = t[u].fa);//记录路径
  while(tp) pushdown(st[tp--]);//下传标记
  while( t[x].fa != tar ) {
    int f = t[x].fa, ff = t[f].fa;
    if(ff != tar) {  ( (rs(ff) == f ^ rs(f) == x)  ? rotate(x) : rotate(f) );  }
    rotate(x);
  }  if( !tar ) rt = x;
}

啊，完了，然后插入什么的就和普通的 BST 一样的。直接写就完事了。

考虑维护数列的时候怎么做呢。大概就是拿下标当键值进行 splay 的建立，然后在多存一个变量表示对应的值。

然后提取区间咋做呢。就你考虑你的 \([l,r]\) 区间被提取，先进行 splay(l)，那么根据性质 \(r\) 肯定在 \(l\) 的右边子树内。

然后你想想如果我们的 \(r+1\) 是 \(l\) 的右儿子，那么 \([l+1,r]\) 就是 \(r+1\) 的左子树了。

但是还留了一个 \(l\) 在外面，好烦啊，，，

那，考虑换顺序和换点提一下，将 \(r+1\) 提到根，然后，将 \(l - 1\) 提到他的左儿子去，那么 \(l - 1\) 的右子树就是区间 \([l,r]\) 了。

然后要对区间加去见翻转啥的，直接提出来打个标记就完了，查询就直接查就完事了。

然后注意因为提取的是 \([l-1,r+1]\) 所以要插入 \(id = 0, n+1\) 的点。

然后完了。那好像基本说完了/jk/jk/jk。

还是多讲几个操作水水字数吧。

splay 进行合并咋做啊。

启发式合并，小的向大的合并，合并 \(n\) 次复杂度为 \(n\log n\) 的。

唔，分裂呢？就，先把区间 \([l,r]\) 提出来，那么 \(l -1\) 为这个区间的父亲。

那么把这个区间和他断绝父子关系就行了。然后就分裂出来了。

然后就完了。感觉很奇怪的是，别人是学 LCT 的时候重新看 splay 才学懂 LCT ，而我好像是学会 LCT 后，才一下搞懂了 splay。。。

然后粘贴一个洛谷模板题的代码：（写的很好看o_O

view code

// 德丽莎你好可爱德丽莎你好可爱德丽莎你好可爱德丽莎你好可爱德丽莎你好可爱
// 德丽莎的可爱在于德丽莎很可爱，德丽莎为什么很可爱呢，这是因为德丽莎很可爱！
#include <bits/stdc++.h>
#define int long long
using namespace std;
#define FOR(i, l, r) for(int i = (l); i <= r; ++i)
#define REP(i, l, r) for(int i = (l); i <  r; ++i)
#define DFR(i, l, r) for(int i = (l); i >= r; --i)
#define DRP(i, l, r) for(int i = (l); i >  r; --i)
#define FORV(i, ver) for(int i = 0; i < ver.size(); i++)
#define FORP(i, ver) for(auto i : ver)
template<class T>T min(const T &a, const T &b) {return a < b ? a : b;}
template<class T>T max(const T &a, const T &b) {return a > b ? a : b;}
template<class T>bool chkmin(T &a, const T &b) {return a > b ? a = b, 1 : 0;}
template<class T>bool chkmax(T &a, const T &b) {return a < b ? a = b, 1 : 0;}
inline int read() {
  int x = 0, f = 1;  char ch = getchar();
  while( !isdigit(ch) ) { if(ch == '-') f = -1;  ch = getchar();  }
  while( isdigit(ch) ) {  x = (x << 1) + (x << 3) + (ch ^ 48);  ch = getchar();  }
  return x * f;
}
const int N = 5e6, inf = 2e10;
int n, rt, tot;
struct node {
  int val, siz, cnt, sum;
  int ch[2], fa;
} t[N];
#define ls(x) t[x].ch[0]
#define rs(x) t[x].ch[1]
void pushup(int p) {
  t[p].siz = t[ls(p)].siz + t[rs(p)].siz + t[p].cnt;
}
void rotate(int x) {
  int f = t[x].fa, ff = t[f].fa;
  int c = rs(f) == x;
  int d = t[x].ch[c ^ 1]; 
  if(ff) t[ff].ch[rs(ff) == f] = x;
  t[x].fa = ff;
  t[f].fa = x;
  t[x].ch[c ^ 1] = f;
  t[f].ch[c] = d; 
  t[d].fa = f;
  pushup(f);  pushup(x);
}
void Splay(int x, int tar) {
  while( t[x].fa != tar ) {
    int f = t[x].fa, ff = t[f].fa;
    if(ff != tar) {
      ( ( (rs(ff) == f) ^ (rs(f) == x) ) ? rotate(x) : rotate(f) );
    }
    rotate(x);
  }
  if(!tar) rt = x;
}
int Find(int x) {
  int u = rt;
  while(t[u].val != x && t[u].ch[t[u].val < x]) u = t[u].ch[t[u].val < x];
  Splay(u, 0);  return u;
}
void insert(int x) {
  int u = rt, fa = 0;
  while(u && t[u].val != x) fa = u, u = t[u].ch[t[u].val < x];
  if(u) t[u].cnt++, t[u].siz++, Splay(u, 0);
  else {
    ++tot;
    t[tot].val = x;  t[tot].fa = fa;  t[tot].cnt = t[tot].siz = 1;
    if( fa ) t[fa].ch[t[fa].val < x] = tot;
    Splay(tot, 0);
  }
}
int Rank(int x) {
  int u = rt;
  while(1) {
    if(t[ls(u)].siz >= x) u = ls(u);
    else if(t[ls(u)].siz + t[u].cnt >= x) return u;
    else x -= t[ls(u)].siz, x -= t[u].cnt, u = rs(u);
  }
}
int Pre(int x) {
  Find(x);
  if(t[rt].val < x) return rt;
  int u = t[rt].ch[0];
  while(u && t[u].ch[1]) u = t[u].ch[1];
  Splay(u, 0);
  return u;
}
int Next(int x) {
  Find(x);
  if(t[rt].val > x) return rt;
  int u = t[rt].ch[1];
  while(u && t[u].ch[0]) u = t[u].ch[0];
  Splay(u, 0);
  return u;
}
void Del(int x) {
  int p = Pre(x), q = Next(x);
  Splay(p, 0);  Splay(q, p);
  int u = t[q].ch[0];
  if(t[u].cnt > 1) t[u].cnt--, t[u].siz--, Splay(u, 0);
  else {  t[q].ch[0] = 0;  }
}
signed main () {
  n = read();  insert(-inf), insert(inf);
  FOR(i, 1, n) {
    int op = read(), x = read();
    if(op == 1) {
      insert(x);
    }
    if(op == 2) {            
      Del(x);
    }
    if(op == 3) { 
      insert(x);  Find(x); printf("%d\n", t[ls(rt)].siz); Del(x);
    }
    if(op == 4) {
      printf("%d\n", t[Rank(x + 1)].val);
    }
    if(op == 5) {
      printf("%d\n", t[Pre(x)].val);
    }
    if(op == 6) {
      printf("%d\n", t[Next(x)].val);
    }
  }
  return 0;
}