菜鸡Pt的 2-sat 学习笔记

1.前言：

讲的不清楚一定要快评论下来，然后这样蒟蒻思考了给大佬一点启发。

2.正文：

\(2-sat\) 是什么呢？

其实就是这样的，\(2-sat\) 问题是形如： 有 \(n\) 个人，每个人可以是男的和女的，要满足他们之间的一类关系，比如 \(i\) 和 \(j\) 中一个是男的，一个是女的。或者都是男的，或者都是女的。让你对他们安排性别满足条件。

用正式一点的话就是，有 \(n\) 个布尔变量，每个变量可以为 \(0\) 或者 \(1\) 。让你去安排每个变量是 \(0\) 还是 \(1\) ，去满足约束条件。

当然有 \(2-sat\) 就有 \(k-sat\) 等，但是目前 \(k > 2\) 是只有暴力枚举解决的问题。

我们谈谈 \(2-sat\) 的问题是怎么解决的。

这里我们先引入一道例题

我们发现这道题里面，是一个很裸的 \(2-sat\) ，我们思考每个变量之间的关系。

我们首先发现的是每一个点，只有 \(2\) 个变量取值，我们考虑把每个变量 \(i\) 拆成两个点 \(i\) 与 \(i+n\) 。表示两个点是 \(\text{true}\) 还是 \(\text{false}\) 。

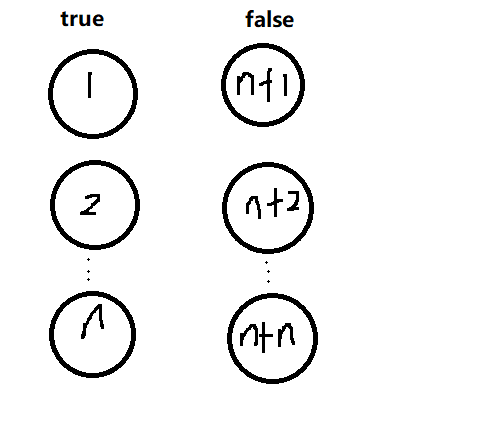
然后我们去考虑对于每一条限制怎么做。

如果有 \(a\) & \(b=0\)。

这个表明了 \(a\) 与 \(b\) 里面一定有一个是 \(0\) 。

那么我们要在 \(a\) 的 \(true\) 里 连边向 \(b\) 的 \(false\) 。并且将 \(b\) 的 \(true\) 连向 \(a\) 的 \(false\) 。

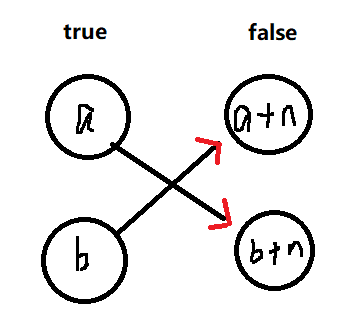
这样可以保证的是无论这两个的取值是怎样，反正最终会有一个走向 \(false\) 。所以这个建边是没问题的，这里应该没问题。

但是，有问题就是我们为什么不能去，从 \(b\) 的 \(false\) 连向 \(a\) 的 \(true\) 。

这么乍一看也没什么问题啊？

但是这样不行的，因为如果 \(b\) 为 \(false\) 其实 \(a\) 为 \(true\) 还是 \(false\) 都是没问题的。而这么连边就是不明确的关系，让人认为，选了\(b\) 为 \(false\) 则 \(a\) 就只能为 \(true\) 了，所以不行。

那么建图是怎样的呢？大概描述一下流程的话。就是：

  • \(a,b\) 不能同时选，那么选了 \(a\) 就要选 \(b+n\) ，选了 \(b\) 就要选 \(a+n\) 则 \(a\rightarrow b+n\) 和 \(b \rightarrow a+n\)
  • \(a,b\) 必须同时选，那么选了 \(a\) 就要选 \(b\) ，选了 \(b\) 就要选 \(a\) 。则 \(a\rightarrow b\) 和 \(b \rightarrow a\)
  • \(a,b\) 中至少选一个，那么选了 \(a\) 就要选 \(b+n\) ，选 \(b\) 就要选 \(a+n\) ，选了 \(a+n\) 就要选 \(b\) ，选了 \(b+n\) 就要选 \(a\) 。则 \(a\rightarrow b+n\) 和 \(b \rightarrow a+n\) 和 \(a+n \rightarrow b\) 和 \(b+n \rightarrow a\)
  • \(a,b\) 中 \(a\) 必须选，那么让 \(a+n \rightarrow a\)

然后就可以了完成建图过程，但是我们还需要知道是否存在分派方案和怎么分配。

怎么去判断是否有解，在 \(\text{hl666}\) 神仙的博客里学到了两种方法。

第一种：\(\text{DFS}\)
  1. 对于每个不确定的变量 \(a_i\) ，令其为0，然后沿边访问相连的点。
  2. 检查是否会导致任意一个 \(b\) 与 \(b+n\) 都被选中，如果不会那么撤销让 \(a_i=0\)
  3. 否则让 \(a_i=1\) 重复 \(2\) 操作。
  4. 继续考虑不确定的限制

复杂度为 \(n^2+nm\) ，可以用 \(bitset\) 优化传递闭包后进行 \(\dfrac{n^3}{w}\) 的预处理做到 \(n+m\) 的 DFS 。

这样做可以保证求解出的答案字典序最小。

第二种：\(\text{Tarjan}\)

无解的情况其实就是某一变量的 \(false\) 走到 \(true\) 而从 \(true\) 也能走到 \(false\) 也就是一个变量的取值在同一强连通分量内就无解。

而且分析一下，你还可以知道，在同一强连通分量内的变量取值相同。

怎么去求解取值呢？

我们要选的其实就是在图中被边指着的变量值，这样才可以保证不会产生矛盾。

那么在拓扑序上就是我们要选择拓扑序上较大的值。

因为在有向图中拓扑排序后，被指向的点的拓扑序大于指向它的点。

但是其实在求解 \(\text{Tarjan}\) 时已经求解除了拓扑序，只不过时反向的，可以思考 $\text{Tarjan} $ 的过程理解。

然后取两个取值中强连通分量的编号较小的所对应的值就可以了。

时间复杂度为 \(n+m\)

下面给出例题代码的参考实现：


#include<bits/stdc++.h>
using namespace std;
#define MAXN 900
struct ios_in{
 inline char gc(){
  static char buf[MAXN],*l,*r;
  return (l==r)&&(r=(l=buf)+fread(buf,1,MAXN,stdin),l==r)?EOF:*l++;
 }
 template <typename _Tp>
 inline ios_in&operator>>(_Tp&x){
  static char ch,sgn;
  for(sgn=0,ch=gc();!isdigit(ch);ch=gc()) {
   if(!~ch) return *this;
   sgn|=ch=='-';
  }
  for(x=0;isdigit(ch);ch=gc()) x=(x<<1)+(x<<3)+(ch^'0');
   sgn&&(x=-x);
   return *this;
 }
}Cin;
const int N = 3e6;
int n,m,x[N];
int dfn[N],low[N],cnt,nex[N],first[N],v[N],num;
int ins[N],tp,sc,scc[N],sz[N],s[N];
//scc[i]表示i所在scc的编号
void add(int from,int to){nex[++num]=first[from];first[from]=num;v[num]=to;	}
void tarjan(int u){
 low[u]=dfn[u]=++cnt;s[++tp]=u;ins[u]=1;
 for(int i=first[u];i;i=nex[i]){
  int to=v[i];
  if(!dfn[to]){
   tarjan(to);
   low[u]=min(low[u],low[to]);	
  }
  else if(ins[to]){
   low[u]=min(low[u],dfn[to]);	
  }	
 }
 if(dfn[u]==low[u]){
  ++sc;
  while(s[tp]!=u){
   scc[s[tp]]=sc;
   sz[sc]++;
   ins[s[tp]]=0;
   --tp;	
  }
  scc[s[tp]]=sc;
  sz[sc]++;
  ins[s[tp]]=0;
  --tp;	
 }	
} 
signed main(){
 Cin>>n>>m;
 for(int i=1;i<=m;i++){
  int a,b,c,d;
  Cin>>a>>c>>b>>d;
  if(c&&d){
   add(a,b+n);
   add(b,a+n);	
  }
  if(!c&&!d){
   add(a+n,b);
   add(b+n,a);	
  }
  if(c&&!d){
   add(a,b);
   add(b+n,a+n);	
  }
  if(!c&&d){
   add(a+n,b+n);
   add(b,a);	
  }	
 }
 for(int i=1;i<=2*n;i++)
  if(!dfn[i]) tarjan(i);	
 
 for(int i=1;i<=n;i++)
  if(scc[i]==scc[i+n]){printf("IMPOSSIBLE");return 0;}	
 
 printf("POSSIBLE\n");
 for(int i=1;i<=n;i++){
  if(scc[i]>scc[i+n]){//强连通分量小，拓扑序大，答案优秀 
   printf("1 "); 	
  }
  else printf("0 ");	
 }
 return 0;	
}

下面有思路一样的双倍经验。

不过要注意对字符串后面数字的处理要处理完，它不止一位。

到此就介绍完了 \(2-sat\) 算法，下面会更新一下例题辅助理解，期待！

3.杂题选做：

题目：洛谷P6378

题解：

我们发现这道题其实就是说要我们选择一些点把他们的点权赋值为 \(1\) ，然后使得图中被划分的 \(k\) 个部分每个部分中只有一个点的点权为 \(1\) 。

那么这就是个经典的 \(2-SAT\) 问题，首先拆点，然后分析。

我们将所有与他有边的视为一个关系。由于保证了一个部分中只有一个关键点，所以对于每一个点，与他相连的那个点之间，他们是不能同时选的，这样就可以两两连边。

考虑每一个部分之间，这也是同理的，可以让每个部分中的点都与划分部分中其他点连上边。

但是这样建图显然不行，是 \(O(n^2)\) 的。

于是考虑用一些技巧，前缀优化建图，然后就可以过了。

#include<bits/stdc++.h>
#define int long long
using namespace std;
inline char nc(){
 static char buf[100000],*p1=buf,*p2=buf;
 return p1==p2&&(p2=(p1=buf)+fread(buf,1,100000,stdin),p1==p2)?EOF:*p1++;
}
inline int read(){
 char ch=nc();int sum=0;
 while(!isdigit(ch))ch=nc();
 while(isdigit(ch))sum=sum*10+ch-48,ch=nc();
 return sum;
}
const int N = 8e6 ,inf =1e12;
int n,m,k,w;
int nex[N],first[N],v[N],num;
void add(int from,int to){nex[++num]=first[from];first[from]=num;v[num]=to;}
int dfn[N],low[N],cnt;
int ins[N],tp,sc,scc[N],sz[N],s[N];
//scc[i]表示i所在scc的编号
void tarjan(int u){
 low[u]=dfn[u]=++cnt;s[++tp]=u;ins[u]=1;
 for(int i=first[u];i;i=nex[i]){
  int to=v[i];
  if(!dfn[to]){
   tarjan(to);
   low[u]=min(low[u],low[to]);	
  }
  else if(ins[to]){
   low[u]=min(low[u],dfn[to]);	
  }	
 }
 if(dfn[u]==low[u]){
  ++sc;
  while(s[tp]!=u){
   scc[s[tp]]=sc;
   sz[sc]++;
   ins[s[tp]]=0;
   --tp;	
  }
  scc[s[tp]]=sc;
  sz[sc]++;
  ins[s[tp]]=0;
  --tp;	
 }	
} 
int las,now;
int pre(int x){return x+n*2;}
int pre2(int x){return x+n*3;}

signed main(){
 n=read(),m=read(),k=read();
 for(int i=1;i<=m;i++){
  int a,b;
  a=read(),b=read();
  add(a+n,b);add(b+n,a);	
 }
 for(int i=1;i<=k;i++){
  w=read(),las=read();
  add(las,las+2*n),add(las+3*n,las+n);
  for(int j=2;j<=w;j++){
   now=read();
   add(now,now+2*n),add(now+3*n,now+n);
   add(las+2*n,now+2*n),add(las+2*n,now+n);
   add(now,las+3*n),add(now+3*n,las+3*n);
   las=now;	
  }
 }
 for(int i=1;i<=4*n;i++) if(!dfn[i]) tarjan(i);	
 for(int i=1;i<=n;i++)
  if(scc[i]==scc[i+n]){puts("NIE");return 0;}	
 puts("TAK");
 return 0;	
}

4.参考资料：

2-SAT超入门讲解

2-SAT总结

2-sat研究

posted @ 2021-07-21 20:38  Pitiless0514  阅读(135)  评论(4)    收藏  举报