组合数学

组合数学书攻略

组合数学：

前置芝士：

平方和公式： \(1^2+2^2+\cdots+n^2=\frac{n(n+1)(2n+1)}{6}\)

概念与计数：

基本计数原理：

分类计算加法原理，分布计算乘法原理。

简单容斥与摩根定理：

• \(\begin{vmatrix}A\cup B\end{vmatrix}=\begin{vmatrix}A\end{vmatrix}+\begin{vmatrix}B\end{vmatrix}-\begin{vmatrix}A\cap B\end{vmatrix}\)
• \(\begin{vmatrix}A\cup B\cup C\end{vmatrix}=\begin{vmatrix}A\end{vmatrix}+\begin{vmatrix}B\end{vmatrix}+\begin{vmatrix}C\end{vmatrix}-\begin{vmatrix}A\cap B\end{vmatrix}-\begin{vmatrix}A\cap C\end{vmatrix}-\begin{vmatrix}C\cap B\end{vmatrix}+\begin{vmatrix}A\cap B\cap C\end{vmatrix}\)

\[\left| \bigcup_{i=1}^n A_i\right|=\sum_{\varnothing\not={\rm J}\subseteq\{1,\cdots,n\}}(-1)^{\begin{vmatrix}{\rm J}\end{vmatrix}+1}\left| \bigcap_{{\rm j}\in{\rm J}} A_j\right|\\ \]

代码可以利用 \(dfs\) 或状压实现

摩根定理： 交集的补等于补集的并，并集的补等于补集的交。

即 \(\overline{A\cup B}=\overline{A}\cap\overline{B}\) \(\overline{A\cap B}=\overline{A}\cup\overline{B}\)

\[\left| \bigcap_{i=1}^n \overline{A_i}\right|=\sum_{{\rm J}\subseteq\{1,\cdots,n\}}(-1)^{\begin{vmatrix}{\rm J}\end{vmatrix}}\left| \bigcap_{{\rm j}\in{\rm J}} A_j\right|\\\left| \bigcap_{i=1}^n A_i\right|=\sum_{{\rm J}\subseteq\{1,\cdots,n\}}(-1)^{\begin{vmatrix}{\rm J}\end{vmatrix}}\left| \bigcap_{{\rm j}\in{\rm J}} \overline{A_j}\right|\\ \]

组合计数：

排列数：

从 \(n\) 个不同元素中依次取出 \(m\) 个元素排成一列，产生的不同排列的数量为：(取 \(m\) 个，将 \(m\) 个排序)

\[A_n^m(P_n^m)=\frac{n!}{(n-m)!} \]

组合数：

从 \(n\) 个不同元素中取出 \(m\) 个组成一个集合（不考虑顺序），产生的不同集合的数量为：

\[C_n^m= \begin{pmatrix}n\\m\end{pmatrix}=\frac{n!}{m!(n-m)!} \]

性质：

• \(A_n^k=C_n^k\times k!\)
• \(C_n^m=C_n^{n-m}\)
• \(C_n^m=C_{n-1}^m+C_{n-1}^{m-1}\) （杨辉三角）
• \(\frac{k}{n}\times C_n^k=C_{n-1}^{k-1}\)
• \(\sum_{i=0}^nC_n^i=2^n\)
• \(\sum_{i=0}^n(-1)^iC_n^i=0\)

组合数求解：

单个组合数 \(O(n)\)

代码

int C(int n, int k) {
    int p = 1, q = 1;
    for (int i = n - k + 1; i <= n; ++i)
        p *= i;
    for (int i = 1; i <= k; ++i)
        q *= i;
    return p / q;
}

求 \(C_i^j(i\in[0,n-1],j\in[1,i])\) 递推 \(O(n^2)\)

代码

for (int i = 0; i < n; ++i) {
    C[i][0] = 1;
    for (int j = 1; j <= i; ++j) {
        C[i][j] = C[i - 1][j - 1] + C[i - 1][j];
    }
}

二项式定理：

\[(a+b)^n=\sum_{k=0}^nC_n^ka^kb^{n-k}\\(a-b)^n=\sum_{k=0}^n(-1)^kC_n^ka^kb^{n-k} \]

高精组合数：

求 \(C_n^m\) 的值，结果可能很大，没有模数。

\({\rm sol}:\) \(C_n^m=\frac{n!}{m!\times (n-m)!}\) $\therefore $ 所以可以对 \(n!\) 阶乘进行质因数分解为 \(\prod p_i^{c_i}\) （方法在基础数论博客里）然后对 \(m!\) 和 \((n-m)!\) 分别进行质因数分解，每次使 \(c_i\) 减一。最后统计结果。时间复杂度 \(O(n)\) （高精另算）

代码

#include <iostream>
#include <algorithm>
#include <vector>

using namespace std;


const int N = 5010;

int primes[N], cnt;
int sum[N];
bool st[N];


void get_primes(int n)
{
    for (int i = 2; i <= n; i ++ )
    {
        if (!st[i]) primes[cnt ++ ] = i;
        for (int j = 0; primes[j] <= n / i; j ++ )
        {
            st[primes[j] * i] = true;
            if (i % primes[j] == 0) break;
        }
    }
}


int get(int n, int p) // 求n!中 质因子 p 需要累乘的次数 
{
    int res = 0;
    while (n)
    {
        res += n / p;
        n /= p;
    }
    return res;
}


vector<int> mul(vector<int> a, int b)
{
    vector<int> c;
    int t = 0;
    for (int i = 0; i < a.size(); i ++ )
    {
        t += a[i] * b;
        c.push_back(t % 10);
        t /= 10;
    }
    while (t)
    {
        c.push_back(t % 10);
        t /= 10;
    }
    return c;
}


int main()
{
    int a, b;
    cin >> a >> b;

    get_primes(a);//用欧拉筛筛出 [1~a] 范围内的质数 

    for (int i = 0; i < cnt; i ++ )
    {
        int p = primes[i];
        sum[i] = get(a, p) - get(a - b, p) - get(b, p); // C(a,b) 中第 i 个质数需要累乘的次数 
    }

    vector<int> res;
    res.push_back(1);

    for (int i = 0; i < cnt; i ++ ) // 枚举质因子 
        for (int j = 0; j < sum[i]; j ++ ) // 枚举当前质因子的个数 
            res = mul(res, primes[i]); // 做高精度乘低精度 

    for (int i = res.size() - 1; i >= 0; i -- ) printf("%d", res[i]);
    puts("");

    return 0;
}

多重集排列数：

\(k\) 种元素，有 \(n_1\) 个 \(a_1\) ， \(n_2\) 个 \(a_2\) ，\(\cdots\) ， \(n_k\) 个 \(a_k\) 。有多少种排列方案。

\[\frac{(n_1+n_2+\cdots+n_k)!}{n_1!\times n_2!\times\cdots\times n_k!} \]

多重集组合数：

1.\(k\) 种元素，有 \(n_1\) 个 \(a_1\) ， \(n_2\) 个 \(a_2\) ，\(\cdots\) ， \(n_k\) 个 \(a_k\) 。从中取出 \(r\) ( \(\forall i\in[1,k],r\leq n_i\) )个的方案数。

设 \(r\) 个元素构成的集合是 \(\{x_1·a_1,x_2·a_2,\cdots,x_k·a_k\}\)\(\therefore x_1+x_2+\cdots+x_k=r\) 且 \(x_i\geq 0\) (隔板法)答案为 \(C_{r+k-1}^{k-1}\)

2.\(k\) 种元素，有 \(n_1\) 个 \(a_1\) ， \(n_2\) 个 \(a_2\) ，\(\cdots\) ， \(n_k\) 个 \(a_k\) 。从中取出 \(r\) ( \(r\leq \sum_{i=1}^kn_i\) )个的方案数为：

\[C_{k+r-1}^{k-1}-\sum_{i=1}^kC_{k+r-n_i-2}^{k-1}+\sum_{1\leq i<j\leq k}C_{k+r-n_i-n_j-3}^{k-1}-\cdots+(-1)^kC_{k+r-\sum_{i=1}^kn_i-(k+1)}^{k-1} \]

若先不考虑 \(n_i\) 的限制，从 \(S=\{\infty · a_1,\infty · a_2,\cdots,\infty · a_k\}\) 中取出 \(r\) 个元素，则方案数为 \(C_{k+r-1}^{k-1}\)设 \(S_i\) 表示包含至少 \(n_i+1\) 个 \(a_i\) 的多重集，即从 \(S\) 中先取出 \(n_i+1\) 个 \(a_i\)， 然后再任选 \(r-n_i-1\) 个元素构成 \(S_i\) ，可得不同的 \(S_i\) 的数量为 \(C_{k+r-n_i-2}^{k-1}\)那么进一步思考，从 \(S\) 中先取出 \(n_i+1\) 个 \(a_i\) 和 \(n_j+1\) 个 \(a_j\) ，然后再任选 \(r-n_i-n_j-2\) 个元素，构成的集合即为 \(S_i\cap S_j\) ，方案数为 \(C_{k+r-n_i-n_j-3}^{k-1}\)根据容斥原理可得：

\[\left| \bigcup_{i=1}^kS_i \right| =\sum_{i=1}^kC_{k+r-n_i-2}^{k-1}-\sum_{1\leq i<j\leq k}C_{k+r-n_i-n_j-3}^{k-1}+\cdots+(-1)^{k+1}C_{k+r-\sum_{i=1}^kn_i-(k+1)}^{k-1} \]

\[ 故答案为 $C_{k+r-1}^{k-1}-\left|\cup_{i=1}^kS_i\right|$ \]

板子题Devu and Flowers

代码

#include<bits/stdc++.h>
#define ll long long
using namespace std;

inline ll read(){
    ll s=0,k=1;
    char c=getchar();
    while(c>'9'||c<'0'){
        if(c=='-')k=-1;
        c=getchar();
    }
    while(c>='0'&&c<='9'){
        s=(s<<3)+(s<<1)+(c^48);
        c=getchar();
    }
    return s*k;
}

const int mod=1e9+7;
ll a[25],n,m,ans,inv[25];

ll ksm(ll a,ll b){
    ll t=1;
    for(;b;b>>=1,a=a*a%mod)
        if(b&1) t=t*a%mod;
    return t;
}

ll C(ll y,ll x){
    if(x<0||y<0) return 0;
    if(x>y) return 0;
    y%=mod;
    ll ans=1;
    for(int i=0;i<x;i++) ans=ans*(y-i)%mod;
    (ans*=inv[x])%=mod;
    if(y==0) return 1;
    return ans;
}

int main(){
    ll t=1;
    for(int i=1;i<=20;i++) t=t*i%mod;
    inv[20]=ksm(t,mod-2);
    for(int i=19;i>=0;i--) inv[i]=inv[i+1]*(i+1)%mod;
    n=read();m=read();
    for(int i=1;i<=n;i++) a[i]=read();
    for(int j=0;j< 1<<n ;j++){
        if(j==0) ans=(ans+C(n+m-1,n-1))%mod;
        else{
            ll tt=n+m;
            ll s=0;
            for(int i=0;i<n;i++)
                if(j>>i&1){
                    s++;
                    tt-=a[i+1];
                }
            tt-=s+1;
            if(s&1) ans=(ans-C(tt,n-1))%mod;
            else ans=(ans+C(tt,n-1))%mod;
        }
    }
    printf("%lld\n",(ans+mod)%mod);
    return 0;
}

计数技巧：

等价替代（映射）：

构造一个映射，将每一种原问题的方案映射为新问题的一种方案，并使答案更容易计算。例如捆绑法，插空法，隔板法等。

捆绑法： 也成整体法，即若要求若干物品相邻，可以将他们视作一个整体来计数。

插空法： 如果要求若干物品两两不相邻，可以先将其他物品放好，然后将这些物品插入空挡当中进行计数。

隔板法： 将不可区分物品分配问题、不定方程整数解问题转化为插板组合问题。

例： 把 \(n\) 个相同的苹果分给 \(k\) 个人，要求每人至少分到一个的方案数。(求 \(x_1+x_2+x_3+\cdots+x_k=n\) 的整数解，满足 \(x_i\geq 1\))把 \(n\) 个苹果排成一排，从左到右一次插入 \(k-1\) 块板子，共有 \(n-1\) 个位置可以插入，所以答案为 \(C_{n-1}^{k-1}\) 。

改变计数目标：

如果直接按照题意来计数比较困难，可以尝试通过减法、容斥原理等方法转换成容易求的目标。

改变枚举顺序：

很多时候，计数题要做的基本上是:在某个范围内枚举元素，计算它们的和。直接按照题意来做显然只能拿到暴力分(x), 我们往往需要安排一个合适的顺序来计算。

例： 求 \(\sum_{i=1}^n\sum_{j=1}^n\max(i,j)\)

\[\sum_{i=1}^n\sum_{j=1}^n\max(i,j)=\sum_{k=1}^nk\times\sum_{i=1}^n\sum_{j=1}^n[\max(i,j)==k]\ \ \ \ \ \ \ \\=\sum_{k=1}^nk\times(2k-1)\ \ \ \ \\=\sum_{k=1}^n(2n+1)k-k^2\\=\frac{4n^3+3n^2-n}{6}\ \ \ \ \ \]

\[\]

例题：

数字求和：

设 \(f(x)\) 为 \(x\) 在十进制下的各位数字之和，例如 \(f(123) = 1+2+3=6\) ，求

\[\sum_{i=0}^{10^n}f(x) \]

答案对 \(10^9+7\) 取模。

考虑除去 \(10^n\) 这一个数字之外的其他数字中：\(\forall i \in [1,9]\) ，都会在每一位上出现 \(10^{n-1}\) 次。所以这些数字对答案的贡献就是 \(\sum_{i=1}^9i\times n\times 10^{n-1}=45\times n\times 10^{n-1}\)故答案为 \(45\times n\times 10^{n-1}+1\)

圆盘染色：

\(n\) 块组成一个圆盘，用 \(m\) 种颜色染色，使得相邻两块的颜色不同。求方案数。

考虑如果 \(n\) 的颜色与 \(n-2\) 相同，则将 \(n-2,n-1,n\) 看作一个整体。那么 \(n-1\) 块有 \(m-1\) 种选择，则方案数为 \((m-1)\times f(n-2)\) ，（ \(f(i)\) 表示分成 \(i\) 块的方案数）考虑如果 \(n\) 的颜色与 \(n-2\) 不同，将 \(n-2,n-1,n\) 看作一个整体。那么 \(n-1\) 块有 \(m-2\) 种选择，则方案数为 \((m-2)\times f(n-1)\) 。\(\therefore f(n)=(m-1)\times f(n-2)+(m-2)\times f(n-1)\)( \(f(1)=0,f(2)=m\times(m-1),f(3)=m\times (m-2)\) )

数三角形：

给定一个 \(N\times M\) 的网格，请计算三点都在格点上的三角形共有多少个。注意三角形的三点不能共线。

【三角形数量】等于【任选三个点的方案数】减去【三点共线的方案数】****【三点共线的方案数】等于【横着的】加【竖着的】加【斜着的】【横着的】：\((m+1)\times C_{n+1}^3\)【竖着的】：\((n+1)\times C_{m+1}^3\)斜着的直线按斜率正负分为两种，并且这两种的方案数是相等的。因此，我们只需要计算出斜率为正的方案数，再乘以 \(2\) 即可。将核心计算内容——斜率为正的方案数记为 \(ans\) 。假设网格中 \(AB\) 平行于底边 \(x\) 轴，长度为 \(i\) ， \(BC\) 平行于侧边 \(y\) 轴，长度为 \(j\) ，那么 \(AC\) 上的整点数量为 \(\gcd(i,j)-1\) (不算 \(A,C\) 两点)。

\[\therefore ans=\sum_{i=1}^n\sum_{j=1}^m(n-i+1)(m-j+1)(\gcd(i,j)-1) \]

此时还能继续化简：

\[\begin{array}{l} =\sum_{i=1}^n\sum_{j=1}^m(n-i+1)(m-j+1)(\sum_{d\mid \gcd(i,j)}\varphi(d)-1)\\ =\sum_{i=1}^n\sum_{j=1}^m(n-i+1)(m-j+1)\sum_{d\mid\gcd(i,j)}^{d\neq 1}\varphi(d)\\ =\sum_{d=2}^{{\rm min}(n,m)}\varphi(d)\sum_{i=1}^{\lfloor\frac{n}{d}\rfloor}(n-id+1)\sum_{j=1}^{\lfloor\frac{m}{d}\rfloor}(m-jd+1)\\ =\frac{1}{4}\sum_{d=2}^{{\rm min}(n,m)}\varphi(d)(n-d+n\% d+2)\lfloor\frac{n}{d}\rfloor(m-d+m\% d+2)\lfloor\frac{m}{d}\rfloor\\ (等差数列)\end{array} \]

至此可以 \(O(n)\) 求得答案。

Counting swaps：

给定你一个 \(1∼n\) 的排列 \(p\) ，可进行若干次操作，每次选择两个整数 \(x,y\) ，交换 \(px,py\) 。用最少的操作次数将给定排列变成单调上升的序列 \(1,2,\cdots,n\) ，有多少种方式呢？

对于一个排列 \(p_1,p_2,\cdots,p_n\) ，每一个 \(p_i\) 向 \(i\) 连一条无向边，构成一张由若干环组成的无向图，目标状态即为 \(n\) 个自环。

设 \(f[i]\) 表示一个大小为 \(i\) 的环，在保证交换次数最少的情况下，有多少种方法将其变成目标状态。

每一次交换可以把大小为 \(i\) 的环拆成大小为, \(x,y\) 的两个环(\(x+y=n\)) 。设 \(T(x,y)\) 表示有多少种交换方法可以将一个大小为 \(i\) 的环拆成两个大小分别为 \(x,y\) 的环。可以发现：当 \(x=y\) 时， \(T(x,y)=x\) ，否则 \(T(x,y)=x+y\) 。

\(x\) 环需要 \(x−1\) 次交换达到目标状态，同理 \(y\) 环需要 \(y−1\) 次操作，由于 \(x\) 环和 \(y\) 环的操作互不干扰且可以随意排列，因此得到转移方程：

\[f[i]=\sum_{x+y=i}f[x]\times f[y]\times T(x,y)\times \frac{(i-2)!}{(x-1)!\times (y-1)!} \]

(在打表后可发现 \(f[n]=n^{n-2}\))假设排列中有 \(k\) 个大小为 \(L_1,L_2,\cdots,L_k\) 的环，则

\[Ans=(\prod_{i=1}^kf[L_i])\times (\frac{(n-k)!}{\prod_{i=1}^k(L_i-1)!}) \]

算法：

卡特兰数：

其对应序列为：

\[1,1,2,5,14,42,132,429,\cdots,\frac{C_{2n}^n}{n+1} \]

• $ H_n\begin{cases}\sum_{i=1}^nH_{i-1}\times H_{n-i}\ n\geq2,n\in\mathbb{N_{+}}\ 1\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ n=0,1\end{cases} $
• \(H_n=\frac{H_{n-1}\ \times(4n-2)}{n+1}\)
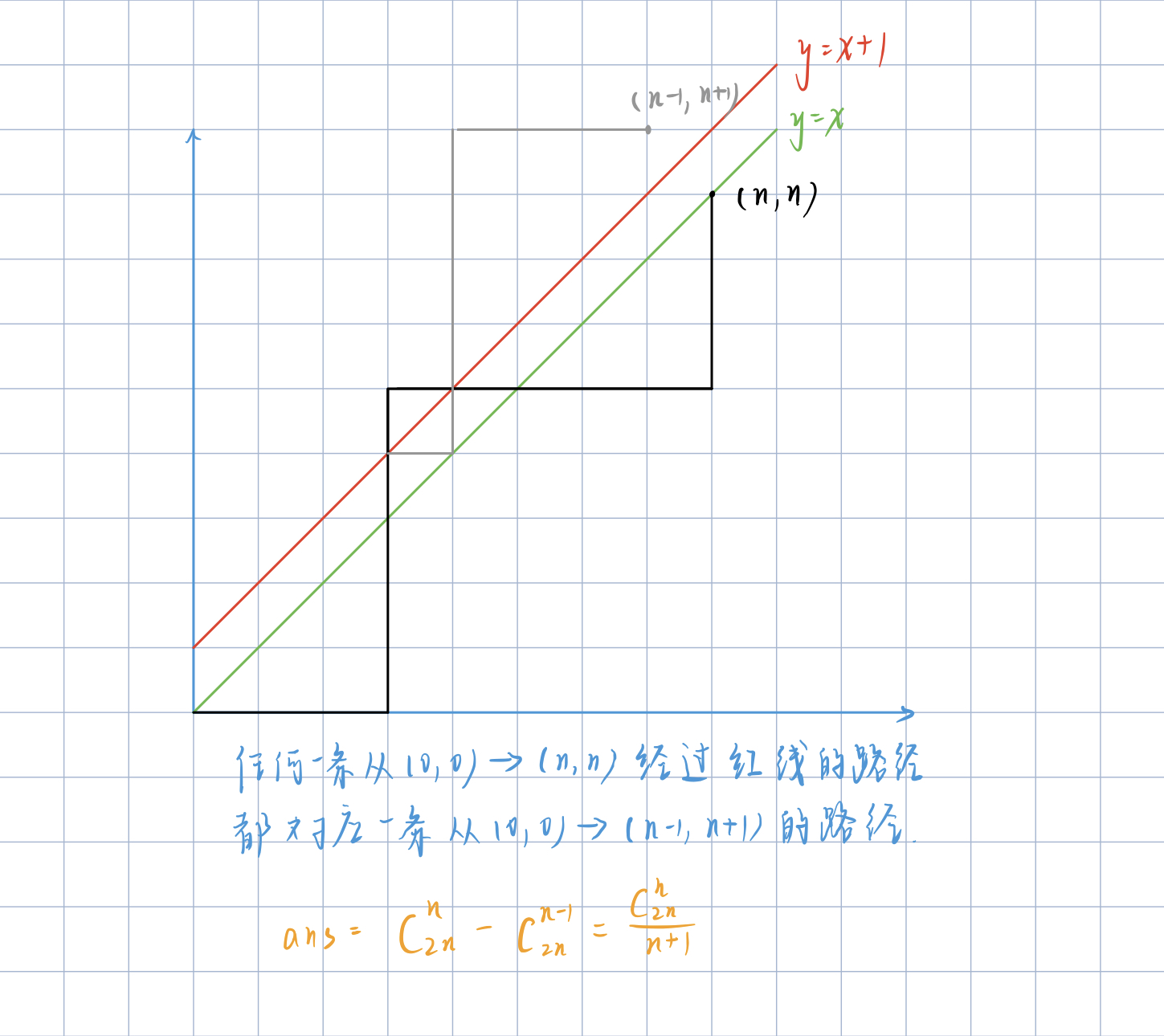
• \(H_n=C_{2n}^n-C_{2n}^{n-1}\)

对于一下问题属于 Catalan 数列：

\(1\).给定 \(n\) 个 \(0\) 和 \(n\) 个 \(1\)，排成的长度为 \(2n\) 的序列，满足任意前缀序列中 \(0\) 的个数都不少于 \(1\) 的个数的序列有多少个。(将 \(01\) 序列置于坐标系中，起点定于原点。若 \(0\) 表示向右走，\(1\) 表示向上走，路径上的任意一点，横坐标大于等于纵坐标的合法路径数量。)



\(2\).一个栈的进栈序列为 \(1,2,3, \cdots ,n\) 有多少个不同的出栈序列？

将进栈视为 \(0\) ，将出栈视为 \(1\) ，则与第一个问题相同，故答案为 \(Cat_n\)

\(3\).\(n\) 个节点，可以构造多少不同二叉树？

设 \(f(n)\) 为 \(n\) 个节点构成的不同二叉树的数量。该问题答案为 不同情况下左子树的方案数 \(\times\) 对应右子树的方案数 的和。即 \(f(n)=f(0)\times f(n-1)+f(1)\times f(n-2)+\cdots+f(n-1)\times f(0)\)会发现 \(f(n)=\sum_{i=1}^nf(i-1)\times f(n-i)\) ，与 \(Cat_n\) 的递推式相同，故答案为 \(Cat_n\) 。

卢卡斯定理/Lucas 定理：

Lucas 定理用于求解大组合数取模的问题，其中模数必须为素数。正常的组合数运算可以通过递推公式求解，但当问题规模很大，而模数是一个不大的质数的时候，就不能简单地通过递推求解来得到答案，需要用到 Lucas 定理。

对于质数 \(p\) 有：

\[\binom{n}{m}\bmod p=\binom{\lfloor n/p\rfloor}{\lfloor m/p\rfloor}\times \binom{n\bmod p}{m\bmod p} \bmod p \]

对于第二部分可以直接求组合数，对于第一部分可以继续递归 \(Lucas\) 。单次时间复杂度 \(O(p\log p)\) ，可以通过预处理达到 \(O(p+\log p)\) 。

代码

#include<bits/stdc++.h>
#define ll long long
using namespace std;

inline ll read(){
    ll s=0,k=1;
    char c=getchar();
    while(c>'9'||c<'0'){
        if(c=='-')k=-1;
        c=getchar();
    }
    while(c>='0'&&c<='9'){
        s=(s<<3)+(s<<1)+(c^48);
        c=getchar();
    }
    return s*k;
}

const int N=1e5+10;
ll T,n,m,p,a[N],b[N];

ll ksm(ll a,ll b){
    ll t=1;
    for(;b;b>>=1,a=a*a%p)
        if(b&1) t=t*a;
    return t;
}

ll init(ll n,ll p){
    a[0]=1;
    for(int i=1;i<=n;i++) a[i]=(a[i-1]*i)%p;
    b[n]=ksm(a[n],p-2);
    for(int i=n-1;i>=0;i--){
        b[i]=b[i+1]*(i+1)%p;
    }
}

ll C(ll n,ll m,ll p){
    if(m>n) return 0;
    return a[n]*b[m]%p*b[n-m]%p;
}

ll Lucas(ll n,ll m,ll p){
    if(!m) return 1;
    return (C(n%p,m%p,p)*Lucas(n/p,m/p,p))%p;
}

int main(){
    T=read();
    while(T--){
        n=read();m=read();p=read();
        init(p-1,p);
        printf("%lld\n",Lucas(n+m,m,p)%p);
    }
    return 0;
}

exLucas：

求 \(C_n^m\bmod d\) ( \(d\) 不一定为质数)

1.

将 \(d\) 质因数分解为 \(d=p_1^{c_1}\times p_2^{c_2}\times\cdots\times p_k^{c_k}\)

\(\forall i,j\in[1,k]\) , \(p_i^{c_i}\) 与 \(p_j^{c_j}\) 互质，所以可以构造出如下同余方程：

\[\begin{cases}a_1\equiv C_n^m\ (\bmod \ p_1^{c_1})\\a_2\equiv C_n^m\ (\bmod \ p_2^{c_2})\\\cdots\\a^k\equiv C_n^m\ (\bmod \ p_k^{c_k})\end{cases} \]

在求出所有的 \(a_i\) 后，就可以利用中国剩余定理求解出 \(C_n^m\) 。

所以问题转化为求出 \(C_n^m\bmod p^\alpha\) 的值。

2.

但是同余方程 \(ax\equiv 1(\bmod \ p)\) (乘法逆元) 有解的充要条件为 \(\gcd(a,p)=1\) 。

然而题目显然无法保证有解，所以无法直接求 \({\rm inv}_{m!}\) 和 \({\rm inv}_{(n-m)!}\)

所以可将原式转化为：

\[\frac{\frac{n!}{p^x}}{\frac{m!}{p^y}\times \frac{(n-m)!}{p^z}}\times p^{x-y-z}\bmod p^\alpha \]

其中 \(x\) 为 \(n!\) 中包含 \(p\) 的个数，\(y,z\) 同理。

3.

若对于一个 \(n\) 可以求出 \(\frac{n!}{p^x}\) ，那么就可以求逆元了，所以现在要求 \(\frac{n!}{p^x}\bmod p^k\) 。

对 \(n!\) 进行变形可得：

\[\begin{array}{l}n!\equiv 1\times 2\times \cdots\times n\\ \equiv (p\times 2p\times \cdots)\times\prod_{i=1,i\not\equiv 0(\bmod p)}^n i\\ \equiv p^{\lfloor\frac{n}{p}\rfloor}\times (\lfloor\frac{n}{p}\rfloor)!\times\prod_{i=1,i\not\equiv 0(\bmod p)}^n i\\ \equiv p^{\lfloor\frac{n}{p}\rfloor}\times (\lfloor\frac{n}{p}\rfloor)!\times(\prod_{i=1,i\not\equiv 0(\bmod p)}^{p^k} i)^{\lfloor\frac{n}{p^k}\rfloor}\times(\prod_{i=p^k\lfloor\frac{n}{p^k}\rfloor,i\not\equiv 0(\bmod p)}^ni)\end{array} \]

上述变形的最后一步是： 在 \(\prod_{i=1,i\not\equiv 0(\bmod p)}^n i\) 中每 \(p^k\) 个数是有循环节的。
比如说 \((1\cdot 2 \cdot 4\cdot 5\cdot 7\cdot 8)(10\cdot 11\cdot 13\cdot 14\cdot 16\cdot 17)(\bmod 3^2)\)
后面的那一部分每个数都是 \((3^2+x)\) 然后相乘，只要乘积中有一项 \(3^2\) 取模之后就是 \(0\)，所以最终只会有全选 \(x\) 的那一项有用，就是和左边一样的项。

设 \(f(n)= \frac{n!}{p^x}(\bmod p^k)\ (f(0)=1)\)

\[\therefore f(n)=f(\lfloor\frac{n}{p}\rfloor)\times(\prod_{i=1,i\not\equiv 0(\bmod p)}^{p^k} i)^{\lfloor\frac{n}{p^k}\rfloor}\times(\prod_{i=p^k\lfloor\frac{n}{p^k}\rfloor,i\not\equiv 0(\bmod p)}^ni)\\ \]

\(p^{\lfloor\frac{n}{p}\rfloor}\) 没有了是因为 \(f\) 的定义是把所有的 \(p\) 除完之后的值，那这一项显然应该包括在分母的 \(p^x\) 中。

\[\therefore 原式= \frac{f(n)}{f(m)f(n-m)}p^{x-y-z}\bmod p^k \]

这样就可以用 \(exgcd\) 求逆元了。

而三个阶乘中 \(p\) 的指数 \(x,y,z\) 是好求的，例如 \(n!\) 中 \(p\) 的个数是 \(x=\sum_i \lfloor\frac{n}{p^i}\rfloor\)。

最后利用中国剩余定理得到答案。
复杂度是 \(O(\sum p_i^{k_i})\) 预处理加 \(O(\omega(p)\log n)\) 的单次询问。\(\omega(n)\) 表示 \(n\) 的质因子个数。

代码

#include<bits/stdc++.h>
#define ll long long
using namespace std;

inline ll read(){
	ll s=0,k=1;
	char c=getchar();
	while(c>'9'||c<'0'){
		if(c=='-') k=-1;
		c=getchar();
	}
	while(c>='0'&&c<='9'){
		s=(s<<3)+(s<<1)+(c^48);
		c=getchar();
	}
	return s*k;
}

ll mod,pk[32],pi[32],cnt;
vector<vector<ll> >fac;

vector<ll> calc(int id){
	ll mod=pk[id];
	vector<ll>fac(mod+1);
	fac[0]=1;
	for(ll i=1;i<=mod;i++){
		fac[i]=fac[i-1];
		if(i%pi[id]) fac[i]=fac[i]*i%mod;
	}
	return fac;
}

void init(ll mod){
	cnt=0;fac.clear();
	for(ll i=2;i*i<=mod;i++)
		if(mod%i==0){
			pi[cnt]=i;
			pk[cnt]=1;
			while(mod%i==0){
				pk[cnt]*=i;
				mod/=i;
			}
			fac.push_back(calc(cnt));
			cnt++;
		}
	if(mod>1){
		pi[cnt]=pk[cnt]=mod;
		fac.push_back(calc(cnt));
		cnt++;
	}
}

ll ksm(ll a,ll b,ll mod){
	ll t=1%mod;
	for(;b>0;b>>=1,a=a*a%mod)
		if(b&1) t=t*a%mod;
	return t;
}

void exgcd(ll a,ll b,ll &x,ll &y){
	if(!b){
		x=1;y=0;
		return ;
	}
	ll tx,ty;
	exgcd(b,a%b,tx,ty);
	x=ty;
	y=tx-a/b*ty;
}

ll inv(ll n,ll mod){
	ll x,y;
	exgcd(n,mod,x,y);
	x=x%mod+mod;
	if(x>=mod) x-=mod;
	return x;
}

ll f(ll n,int id){
	if(!n) return 1;
	ll t=ksm(fac[id][pk[id]],n/pk[id],pk[id]);
	ll p=n%pk[id];
	(t*=fac[id][p])%=pk[id];
	return t*f(n/pi[id],id)%pk[id];
}

ll C(ll n,ll m,int id){
	ll k=0,pi=::pi[id],pk=::pk[id];
	for(ll i=n;i>=1;i/=pi) k+=i/pi;
	for(ll i=m;i>=1;i/=pi) k-=i/pi;
	for(ll i=n-m;i>=1;i/=pi) k-=i/pi;
	ll v=ksm(pi,k,pk);
	if(v==0) return 0;
	return f(n,id)*inv(f(m,id),pk)%pk*inv(f(n-m,id),pk)%pk*v%pk;
}

ll CRT(int n,ll a[],ll pk[]){
	ll ans=0;
	for(int i=0;i<n;i++){
		ans+=a[i]*(mod/pk[i])%mod*inv(mod/pk[i],pk[i])%mod;
		if(ans>=mod) ans-=mod;
	}
	return ans;
}

ll exLucas(ll n,ll m){
	ll a[32];
	for(int i=0;i<cnt;i++) a[i]=C(n,m,i);
	return CRT(cnt,a,pk);
}

int main(){
//	freopen(".in","r",stdin);
//	freopen(".out","w",stdout);
	ll n=read(),m=read();mod=read();
	init(mod);
	printf("%lld",exLucas(n,m));
	return 0;
}

第二类斯特林数：

定义：将 \(n\) 个不同的物品分成 \(m\) 个互不区分的非空组的方案数，记作 \(n \brace m\) 或 \(S(n,m)\)。通式：\({n\brace {m}}=\sum_{i=0}^{m}{(-1)^{m-i}\cdot C^{i}_{m}\cdot i^n}\)递推式：\(S(n,m)=S(n-1,m-1)+S(n-1,m)\times m\)