菱形计数与最值问题

题面

你有一个边长为 \(n\) 的正六边形。它被划分成了若干个边长为 \(1\) 的小等边三角形。
我们希望通过合并若干对有公共边的三角形，把这个六边形变成若干个边长为 \(1\) 的菱形的划分。对于每对三角形之间，它们合并有一个代价，问最小的总代价是多少。
例如下面的图，最佳划分方案是图中绿色的边作为每个菱形的边界。

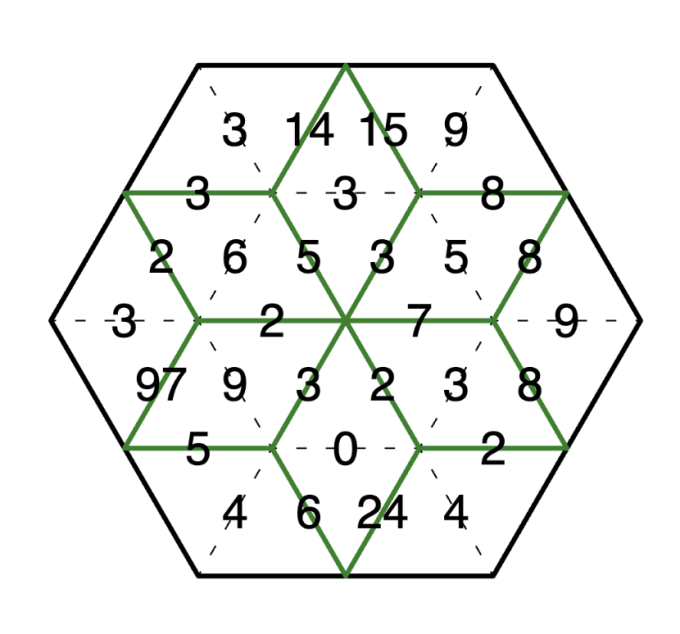
这是最值的题面，还有一个题是求方案数的题目，即：求将边长为 \(a,b,c\) 的正六边形分解成若干小菱形的方案数。

转化为三维问题

相当于一个 \(a\times b\) 的网格，每个格子上可以堆至多 \(c\) 个方块，并且每个格子的方块数量不能超过它左边和上面的格子的方块数量（所以这个题也可以用杨表来做）。

这样就看起来非常直观了，并且每一种放置方案和每一个菱形的划分或者三角形的合并的方案是一一对应的。比如说我们可以看第一个图，那么他三角形合并的方案就是讲图中所有红线两端的三角形合并到一起：

而题目给的那个图就像是这个的第二行第三个图：

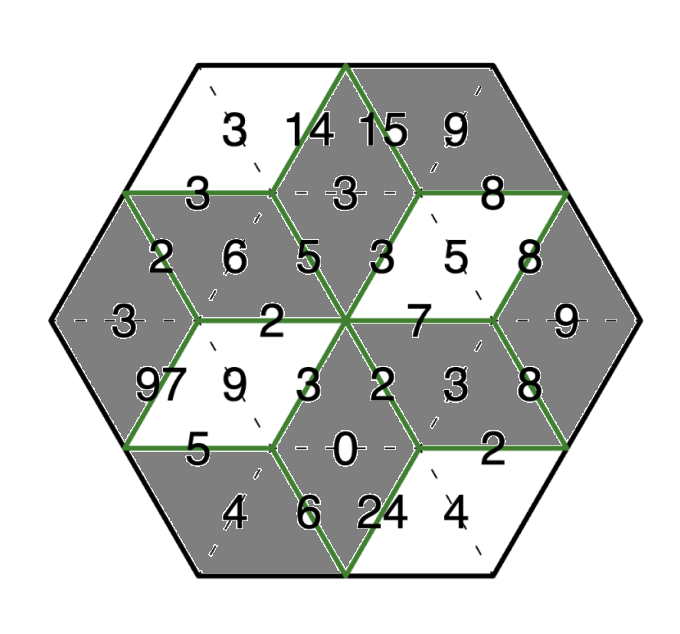
转化为不相交路径问题

将这个问题再转化：从右上角的所有格子往左下角的所有格子对应着走，且路径不相交。



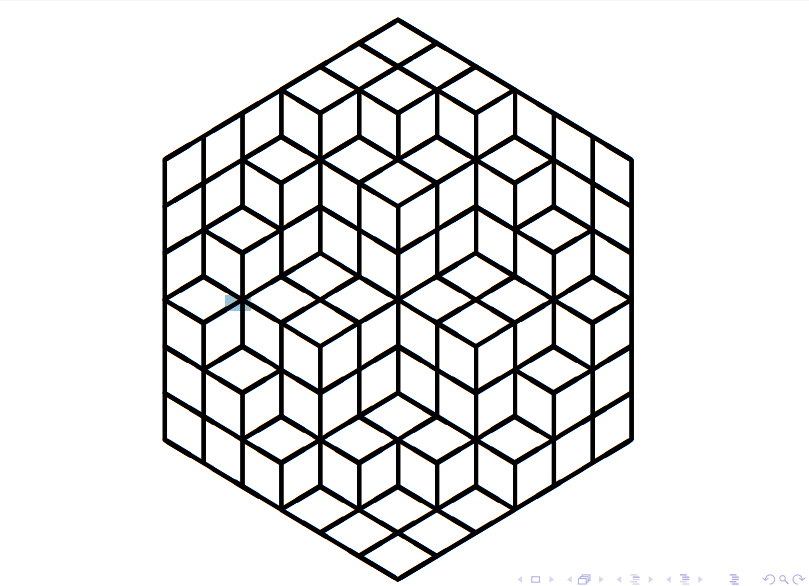
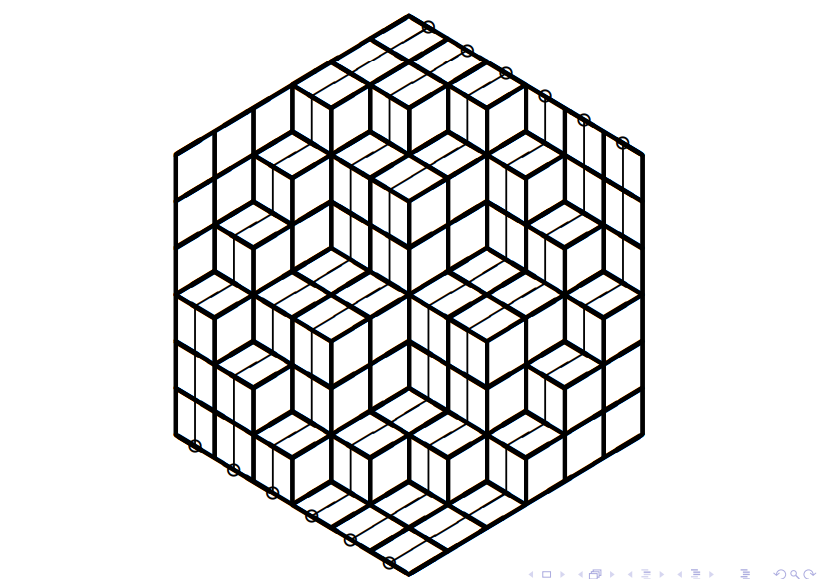
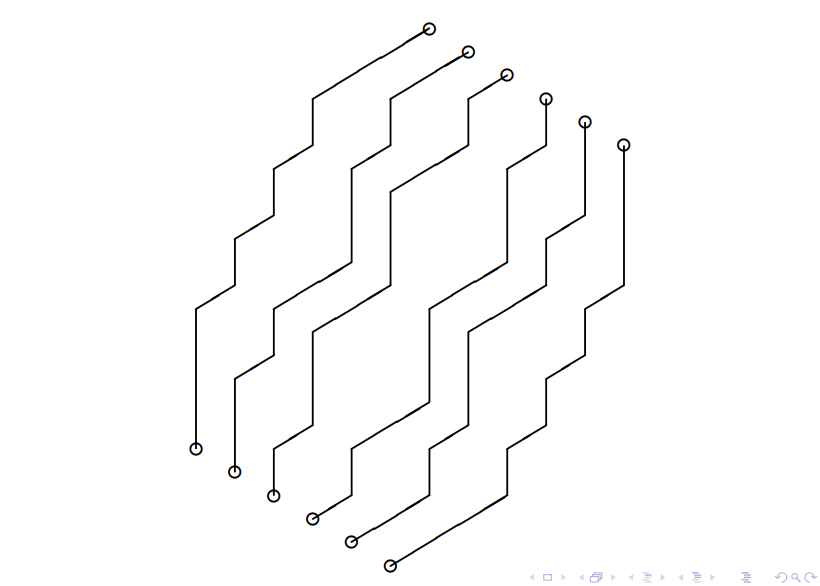
就好像右边的地势比左边要高，我们正在下山，每一个路径直走每个小正方体的上面和前面，而不走他的侧面，显然这种路径的每一种方案和题目所述的合法方案也是对应的——把每条路径的下方点满方块而其余的地方都不填。
此时如果你要求方案数的话就可以直接 \(LGV\) 引理解决。
更具体的可以看 这篇博客

本题的解决方案

但是这个题你要求的是一个最小代价，我们考虑建图费用流。把每个三角形当做点，题目给出的代价当做相邻的那两个三角形对应点之间的边权（显然边的容量都是 \(1\)，构成一个二分图完美匹配）。

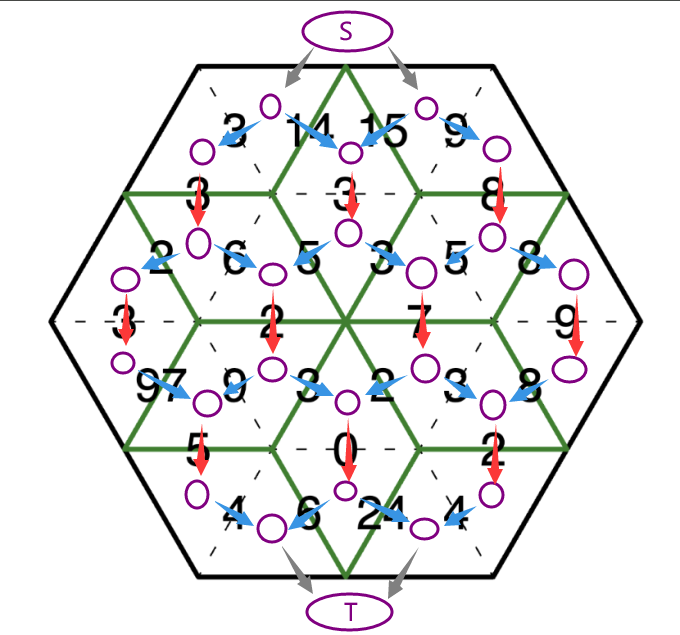
我们把这些边分成两类，一类是上下两个三角形之间的边，即图中红色的边，另一类是其他蓝色的边（\(S,T\) 是源点和汇点，他们向六边形一组对边上对应的点连费用是 \(0\) 的边）。
我们假设每个红色边权的菱形都选了（这显然不合法），然后我们往里填一些小正方形，每一个填不填相当于是破坏了一些竖着的菱形，新添加了一些横着的菱形。
那么我们就可以最开始时把所有红色的边权加到答案里，然后将红色边的边权取负数，蓝色的还是保持正数不变，然后跑 \(n\) 条最小费用的流量，再加上前面所有红色边的边权和就是答案。

注意：跑 \(n\) 条流量是因为我们要找 \(n\) 条路径。
我们同时还要求有流量的路径不交，由于这个图边的容量都是 \(1\) 所以边肯定是不交的。
而且由于这个图的特殊性，一个点最多向外连三条边，所以只要边不交那点肯定不交，因为如果你只相交一个点而边不交的话至少需要四条边，在这个题目中不存在这样的情况。

这个题还毒瘤的要 \(dijkstra\) 费用流。

代码

#include<bits/stdc++.h>
#define ll long long
using namespace std;

inline ll read(){
	ll s=0,k=1;
	char c=getchar();
	while(c>'9'||c<'0'){
		if(c=='-') k=-1;
		c=getchar();
	}
	while(c>='0'&&c<='9'){
		s=(s<<3)+(s<<1)+(c^48);
		c=getchar();
	}
	return s*k;
}

const int N=6e4+10,M=1e5+10;
const ll inf=1e18;
int n,tot,S,T,cnt,pre[N],lst[N],head[N],Start[N];
ll h[N],dis[N];
bool vis[N],nok[M];
struct edge{
	int v,nxt,i;
	ll w;
}e[M];
vector<tuple<int,ll,int> >g[N];

void add(int u,int v,ll w,int i){
	e[++cnt].v=v;
	e[cnt].w=w;
	e[cnt].i=i;
	e[cnt].nxt=head[u];
	head[u]=cnt;
}

void spfa(){
	for(int i=1;i<=tot;i++) dis[i]=inf;
	for(int i=1;i<=tot;i++) vis[i]=0;
	dis[S]=0;
	queue<int>q;
	q.push(S);
	while(!q.empty()){
		int x=q.front();
		q.pop();
		vis[x]=0;
		for(int i=head[x],v;i;i=e[i].nxt){
			v=e[i].v;
			if(dis[v]>dis[x]+e[i].w){
				dis[v]=dis[x]+e[i].w;
				if(!vis[v]){
					vis[v]=1;
					q.push(v);
				}
			}
		}
	}
}

void dijkstra(){
	for(int i=1;i<=tot;i++) dis[i]=inf;
	for(int i=1;i<=tot;i++) vis[i]=0;
	priority_queue<pair<ll,int>,vector<pair<ll,int> >,greater<pair<ll,int> > >q;
	dis[S]=0;
	q.push({0,S});
	while(!q.empty()){
		int x=q.top().second;
		q.pop();
		if(vis[x]) continue;
		vis[x]=1;
		for(int i=head[x],v;i;i=e[i].nxt){
			v=e[i].v;
			if(dis[v]>dis[x]+e[i].w){
				dis[v]=dis[x]+e[i].w;
				pre[v]=x;lst[v]=e[i].i;
				q.push({dis[v],v});
			}
		}
	}
}

ll solve(){
	cnt=0;
	for(int x=1;x<=tot;x++){
		int v,i;
		ll w;
		for(auto z:g[x]){
			tie(v,w,i)=z;
			add(x,v,w,i);
		}
	}
	spfa();
	for(int x=1;x<=tot;x++) h[x]=dis[x];
	ll ans=0;
	for(int siz=1;siz<=n;siz++){
		cnt=0;
		for(int i=1;i<=tot;i++) head[i]=0;
		for(int x=1;x<=tot;x++){
			int v,i;
			ll w;
			for(auto z:g[x]){
				tie(v,w,i)=z;
				if(nok[i]) add(v,x,h[v]-h[x]-w,i);
				else add(x,v,h[x]-h[v]+w,i);
			}
		}
		dijkstra();
		for(int i=1;i<=tot;i++) h[i]+=dis[i];
		ans+=h[T];
		for(int x=T;x!=S;x=pre[x]) nok[lst[x]]^=1;
	}
	return ans;
}

int main(){
//	freopen(".in","r",stdin);
//	freopen(".out","w",stdout);
	n=read();
	for(int i=1;i<=n<<1;i++) Start[i]=n+i/2;
	for(int i=2*n+1;i<=n<<2;i++) Start[i]=Start[4*n+1-i];
	tot=1;
	for(int i=1;i<=n<<2;i++){
		int p=tot;
		tot+=Start[i];
		Start[i]=p;
	}
	Start[(n<<2)+1]=tot;
	for(int i=1;i<=n<<1;i+=2)	{
		int j=Start[i],k=Start[i+1];
		while(j<Start[i+1]){
			ll w=read();
			g[j].push_back(make_tuple(k,w,++cnt));
			w=read();
			g[j].push_back(make_tuple(k+1,w,++cnt));
			j++; k++;
		}
	}
	for(int i=2*n+2;i<=n<<2;i+=2){
		int j=Start[i-1],k=Start[i];
		while(k<Start[i+1]){
			ll w=read();
			g[j].push_back(make_tuple(k,w,++cnt));
			w=read();
			g[j+1].push_back(make_tuple(k,w,++cnt));
			j++; k++;
		}
	}
	ll ans=0;
	for(int i=2;i<n<<2;i+=2){
		int j=Start[i],k=Start[i+1];
		while(j<Start[i+1]){
			ll w=read();
			ans+=w;
			g[j].push_back(make_tuple(k,-w,++cnt));
			j++;k++;
		}
	}
	S=tot;T=++tot;
	for(int i=1,j=Start[n<<2];i<=n;i++){
		g[S].push_back(make_tuple(i,0,++cnt));
		g[j].push_back(make_tuple(T,0,++cnt));
		j++;
	}
	printf("%lld",ans+solve());
	return 0;
}