[Решение] 瑰丽华尔兹

这个人思维和记忆一样差，所以写的更冗长，并且目的是备忘。

原题

洛谷

\(N \cdot M\) 的地图，有若干障碍物，指定 \(K\) 个时间段内只能向指定方向走，单位时间走单位距离或选择不动，问最长路。

入题

从最朴素的角度切入，如果我们使用搜索，枚举所有可能性，自然会产生指数级的状态，且大部分都不优——求最值并不需要劣状态。

考虑缩减状态至多项式级，这是搜索向记忆化，即动态规划转变的标志。

不难想到转移方法：

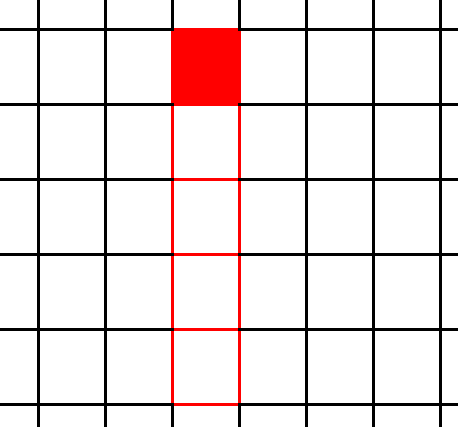
红色填充的格子当前的最长路，可以从包括自身的所有上一个时间段内的格子的最长路（红色边框）转移而来。

若 \((a,b)\) 在指定方向反面，指定时间段 \(k\) 内可以抵达且之间没有障碍物，即：

\[dp(i,j)=\max\limits_{(a,b) \in period(k)} dp(a,b)+distance((i,j),(a,b)) \]

时间复杂度： \(\mathcal O(KNM(N+M))\)

状态数： \(\mathcal O(KNM)\)

空间复杂度可以通过 顺次 处理第 \(k\) 个时间段压缩 \(K\), 为 \(\mathcal O(NM)\)。

其实就是滚动的思想。

优化

转移的时间复杂度是 \(\mathcal O(N+M)\)，不够有效率。

考虑转移是有顺序的，是定向依次转移，并且可转移区间大小指定，考虑滑动窗口-单调队列优化。

时间复杂度： \(\mathcal O(KNM)\)

状态数： \(\mathcal O(KNM)\)

代码与细节

#define rep(i,j,k) for(ri i=(j);i<=(k);i++)
#define Wh while
#define re register
#define cn const
#define ri re int

cn int N = 225;
cn int dx[5]={0,-1,1,0,0},
	   dy[5]={0,0,0,-1,1};
//方向增量
int n,m,cx,cy,k;
//地图大小 起始位置 时间段数
char s[N][N];
//地图
int dp[N][N];
//递推数组
int fr,ed,ans;
//单调队列的起始 答案
struct ele {
	int v,p;
}q[N];
//单调队列
void Proc(int x,int y,int tim,int d) {
	fr=1,ed=0;
	//初始化
	for(ri i=1;x&&x<=n&&y&&y<=m;++i,x+=dx[d],y+=dy[d]) {
		//i 记录相对位置
		if(s[x][y]=='x') fr=1,ed=0;//有障碍物：之前的状态都不可能转移到后面来
		else {
			Wh(fr<=ed&&q[ed].v+i-q[ed].p<dp[x][y]) --ed;//维护的的比较方式就是单调队列排序的方式
			Wh(fr<=ed&&i-q[fr].p>tim) ++fr;//去除时间段外的状态
			q[++ed]={dp[x][y],i};
            //在更新前加入很重要。若队首非自身，而自身转移后再入队，那么从自身转移就和从队首转移相同。
            //若干迭代后，若队首在时间段外，而自身仍在内，此时从自身转移相当于从队首转移，而这不合法，错误。
            //本质上是从第k个时间段转移到同时间段的结果，而实际上应当从第k-1个时间段转移。
			dp[x][y]=q[fr].v+i-q[fr].p;//转移。如果队首不是自身，那队首一定更优，符合单调性；否则得到原来的值。
			ans=std::max(ans,dp[x][y]);//统计答案
		}
	}
}

signed main() {
	read(n,m,cx,cy,k);
	rep(i,1,n) std::cin>>s[i]+1;
	memset(dp,128,sizeof dp);
	//设置为 -INF
	dp[cx][cy]=0;
	//确保只有起始点能出发
	ri x,y,z,tim;
	rep(i,1,k) {
		read(x,y,z);
		//读入区间信息
		tim=y-x+1;
			 if(z==1) rep(j,1,m) Proc(n,j,tim,z);
		else if(z==2) rep(j,1,m) Proc(1,j,tim,z);
		else if(z==3) rep(j,1,n) Proc(j,m,tim,z);
		else          rep(j,1,n) Proc(j,1,tim,z);//从边界开始依次更新
	}
	std::cout<<ans;
	return 0;
}