BUAA ObjectOriented Unit1总结
一句话来说,第一单元的作业就是处理一个表达式,展开其中不必要的括号并尽可能进行化简,从而输出化简后最短的字符串。其中,第一次作业仅需支持幂函数,而第二次作业需要支持简单情况下的三角函数、自定义函数以及求和函数,到了第三次作业,这些函数之间可以互相嵌套而产生递归调用。可以说,这些作业有着非常多的细节需要仔细考量,但总体来说,可以将其分解成三个互相独立的部分:
- 解析输入
- 数学化简
- 输出结果
这三个模块的耦合程度非常低,可分别进行单独调试,遇到了bug也非常容易对其定位并加以解决,至于每次作业的迭代,都只需分别对这三个部分进行修改,无需进行大幅度重构。(此处省略几万字自卖自夸......)
第一次作业
代码部分
架构分析
解析输入
在第一次作业中,数据结构为三个部分:
- Expr\(\rightarrow\)Term \(|\) Expr \(\pm\) Term
- Term \(\rightarrow\) Factor \(|\) Term \(\times\) Factor
- Factor \(\rightarrow\) Number \(|\) Pow \(|\) Expr
通过这三个部分就可以把数据存储起来。那怎么处理带指数的Expr呢?我的做法是,当场读,当场解析,读到带指数的Expr时,我返回的是指数个Factor(当然,指数为0就让整体直接返回1),这样一处理,就没有带指数的Expr了。
按照上述的数据结构,使用递归下降的方法就能轻松地完成输入的解析。值得一提的是,如果想要支持Wrong Format!的输出,就要对解析到的每一个单元进行格式判断,使得代码变长,但如果预先假定所有的输入都是符合规范的,就可以省去很多不必要的麻烦。
数学化简
第一次作业的化简还是比较简单的,首先是使用Expr.addsimplify()方法遍历Expr的每一个Term,看看是否有Factor是Expr的形式(也就是是否有括号),如果有,那就对该Term使用Term.multsimplify()的方法进行化简,返回一个新的(也就是拆完括号后的)Expr,而Term.multsimplify()中涉及到Factor和Expr之间的相乘,普通的乘法(Factor乘Expr)可以直接用ArrayList的add方法进行实现,唯一要考虑的就是Expr和Expr的相乘。因此需要构造Expr.mult()方法来分别遍历两个Expr的Term,通过合并Term中装载Factor的ArrayList进行乘法运算,得到新的(也就是乘完后的)Expr,再对该Expr进行递归的化简,之后返回化简后的(也就是无括号的)Expr。如此一来,Expr中就没有括号了,之后通过HashMap储存指数与系数,就可以实现合并同类项,根据合并完同类项的HashMap,就可以返回最终化简后的(也就是无括号,无同类项的)Expr了。
值得一提的是,这种化简方法极大地模拟了人手算的过程,在每一次乘法运算拆括号后都会进行加法运算来合并同类项,极大地减少了运算过程中项的数量,就算是\((1+x)^{1000}\)也能一秒得出结果。而在使用这套方法前,我使用的是另外一套化简方法,该方法基于的是乘法分配律,当我遇到Term中含有Factor是Expr的形式(也就是是含有括号),我就将该Term进行分裂,成为多个新的(也就是不含有该括号的)Term,这种做法虽然代码量极少,但无法在乘法运算拆括号的过程中加入合并同类项的加法运算,导致运算过程中项会非常多,连\((1+x)^{25}\)也会产生爆栈的Error。
输出结果
由于这一次作业的结构非常简单(我懒癌犯了),我就没有写递归的toString方法,而是根据生成的储存指数与系数的HashMap进行输出打印。
性能优化
- 在输出时,系数为1或-1可以进行省略,指数为1可以进行省略
- 指数为2,就可以把\(x\ast\ast2\)化为\(x\ast x\)。
- 如何尽量保证第一项为正呢?我的做法是,如果输出时发现该
Term为负,就append到最后,如果发现该Term为正,就insert到最前面。
分析部分
类图分析
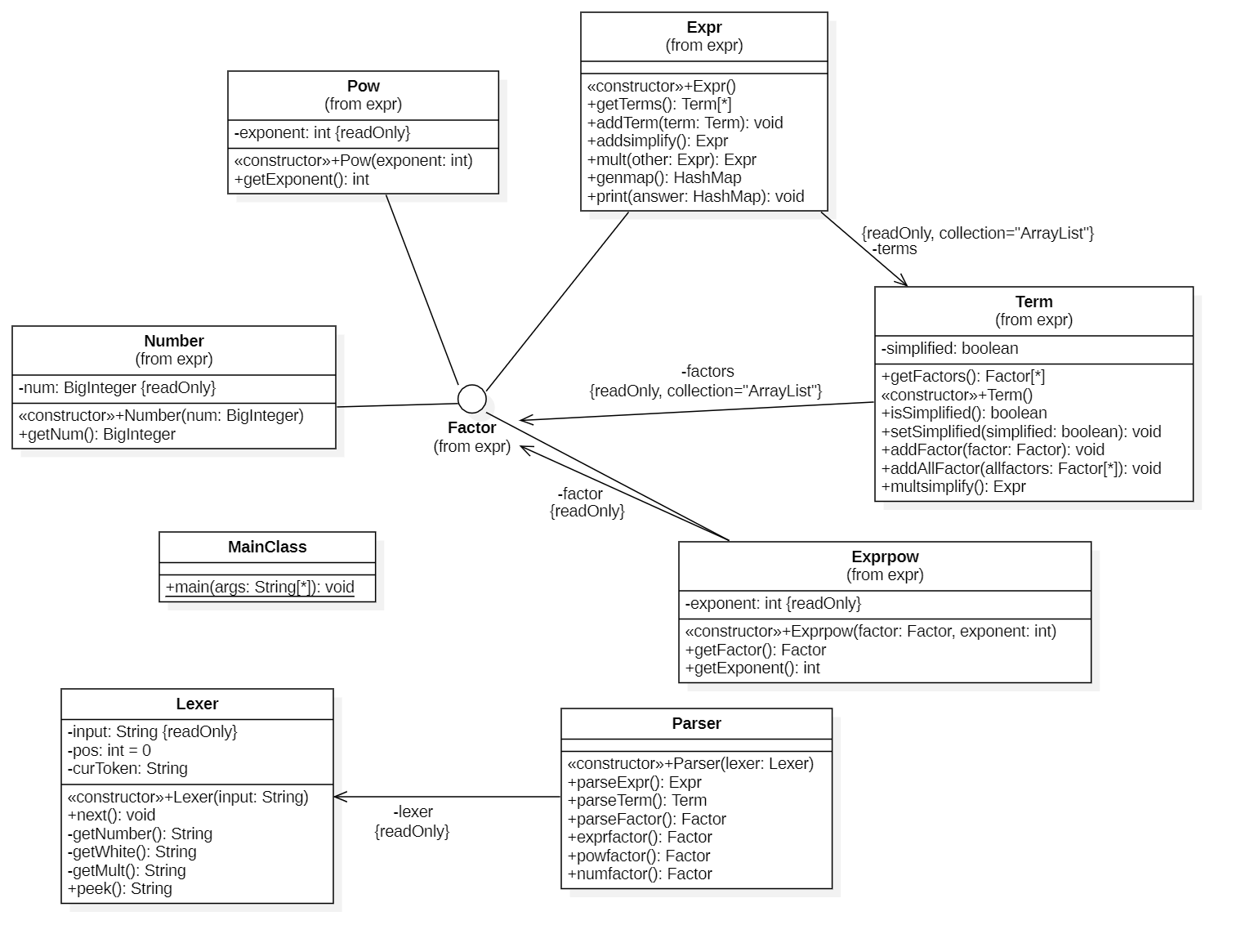
复杂度分析
| Class | OCavg | OCmax | WMC |
|---|---|---|---|
| Parser | 7.571428571428571 | 15.0 | 53.0 |
| MainClass | 1.0 | 1.0 | 1.0 |
| Lexer | 2.3333333333333335 | 6.0 | 14.0 |
| expr.Term | 1.4285714285714286 | 4.0 | 10.0 |
| expr.Pow | 1.0 | 1.0 | 2.0 |
| expr.Number | 1.0 | 1.0 | 2.0 |
| expr.Exprpow | 1.0 | 1.0 | 3.0 |
| expr.Expr | 6.142857142857143 | 18.0 | 43.0 |
| Method | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
| Parser.powfactor() | 14.0 | 4.0 | 7.0 | 7.0 |
| Parser.parseTerm() | 28.0 | 3.0 | 14.0 | 15.0 |
| Parser.Parser(Lexer) | 0.0 | 1.0 | 1.0 | 1.0 |
| Parser.parseFactor() | 3.0 | 3.0 | 3.0 | 3.0 |
| Parser.parseExpr() | 24.0 | 4.0 | 15.0 | 15.0 |
| Parser.numfactor() | 4.0 | 4.0 | 4.0 | 4.0 |
| Parser.exprfactor() | 15.0 | 5.0 | 8.0 | 8.0 |
| MainClass.main(String[]) | 0.0 | 1.0 | 1.0 | 1.0 |
| Lexer.peek() | 0.0 | 1.0 | 1.0 | 1.0 |
| Lexer.next() | 6.0 | 2.0 | 5.0 | 7.0 |
| Lexer.Lexer(String) | 0.0 | 1.0 | 1.0 | 1.0 |
| Lexer.getWhite() | 3.0 | 1.0 | 3.0 | 4.0 |
| Lexer.getNumber() | 2.0 | 1.0 | 3.0 | 3.0 |
| Lexer.getMult() | 2.0 | 1.0 | 3.0 | 3.0 |
| expr.Term.Term() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Term.setSimplified(boolean) | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Term.multsimplify() | 7.0 | 1.0 | 4.0 | 4.0 |
| expr.Term.isSimplified() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Term.getFactors() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Term.addFactor(Factor) | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Term.addAllFactor(ArrayList) | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Pow.Pow(int) | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Pow.getExponent() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Number.Number(BigInteger) | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Number.getNum() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Exprpow.getFactor() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Exprpow.getExponent() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Exprpow.Exprpow(Factor, int) | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Expr.print(HashMap) | 51.0 | 1.0 | 18.0 | 18.0 |
| expr.Expr.mult(Expr) | 4.0 | 1.0 | 4.0 | 4.0 |
| expr.Expr.getTerms() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Expr.genmap() | 12.0 | 1.0 | 6.0 | 6.0 |
| expr.Expr.Expr() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Expr.addTerm(Term) | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Expr.addsimplify() | 42.0 | 1.0 | 13.0 | 13.0 |
从总体来说,Parser和Expr的复杂度较高,其他类的复杂度很低。具体原因是因为我在这两个块中实现了一些初步化简功能,虽然复杂度变高了,维护成本大了,但我认为这种做法会让我思路更清晰。但最大的败笔就是print方法,由于该方法是我偷懒写出来的输出方法,导致模块设计复杂度和圈复杂度很高。这也导致我在之后必须舍弃这个方法,重新写toString方法。
测试部分
自测
- 和室友合作搞了一个自动评测机(基于
python的sympy),使用相同的递归下降构造表达式,之后将输出结果和sympy展开后的结果进行字符串对比 - 手造了几组较小的数据进行测试,比如
0,x,1-1之类的
在自测部分中,使用自动评测机跑了非常久,便认为几乎没有bug了
互测
公测和互测中均未被Hack,且没有丢性能分。但是在房间中成功找出了别人的1个bug,该bug是由于该同学直接使用字符串替换将\(1*x\)替换为\(x\),而没有考虑完全,比如\(81*x\)中的\(1*x\)就不应该进行这样的替换。
第二次作业
代码部分
架构分析
在第二次作业中,需要额外支持sin和cos的三角函数,f(...)、g(...)、h(...)的自定义函数,sum的求和函数,同时,需要支持简单的括号嵌套(srds在第一次作业中我就已经支持括号嵌套了),同时对于新加的三个函数的数据加入了一些限制,比如Factor不能是Expr等(srds我觉得第三次作业一定会支持,就在第二次作业中也支持了)。由于我的架构较好,所以只需加一些代码,不用打补丁重构啥的。
解析输入
在第二次作业中,数据结构为五个部分:
- Expr\(\rightarrow\)Term \(|\) Expr \(\pm\) Term
- Term \(\rightarrow\) Factor \(|\) Term \(\times\) Factor
- Factor \(\rightarrow\) Number \(|\) Pow \(|\) Expr \(|\) Function
- Function \(\rightarrow\) Diyfunction \(|\) Sumfunction \(|\) Trifunction
- Totaldiyfunctions
相比于第一次作业,新增了Function接口,并使其继承Factor接口,用以储存新增的三种函数Diyfunction(自定义函数)、Sumfunction(求和函数)、Trifunction(三角函数)。同时,还新增了一个比较独立的类Totaldiyfunctions用于储存自定义函数的定义式。
相比于第一次作业,由于新增了三种函数,需要对原来递归下降的解析进行修改,我的做法是,当场解析,当场代入,也就是说,在解析到三种函数时,我调用该函数的simplify方法来对函数进行化简,返回化简后的Factor,这样的话,之后就没有任何后顾之忧。当然,难点就来到了每种函数的simplify方法了,除了Trifunction只需对里面的内容进行化简外,Diyfunction和Sumfunction均需要使用替换带入的方法,一种简单又省事的办法就是直接使用字符串替换(干净又卫生啊),但我觉得这样不够优雅(其实是因为我觉得需要考虑字符串有重合部分,比如sin和i,还要考虑代入要加括号啥的太麻烦了,怕出bug),于是,我就使用了数据结构层面的递归代入,但这样做需要有一个致命前提,就是你每想实现一次代入,就要深拷贝一份新的函数内容出来,于是我就对每个类写了一个copy方法(因为我用不来自带的clone方法啊),在这些基础上,就可以实现递归的代入,在代入完成后,化简一次,目的还是如第一次作业中所说,减少项的数量,让程序能跑更大的数据,跑得更快。
值得一提的是,由于新加入了三种函数,导致原来的方法会变长,很不雅观(代码风格被扣分了),所以我删除了部分Wrong Format!的拓展。
数学化简
由于函数在解析时已经进行化简了,所以相比于第一次作业来说,只需修改Term的化简和Expr的化简。
既然解析时已经做了函数的化简了,那数学化简部分第二次作业比第一次作业多了啥呢?答案是Trifunction。由于它的存在,不能简单地只储存系数和指数了,所以在Term中需要新写一个merge方法,该方法基于HashMap实现,该HashMap存储的是基元和指数,分别通过getRadix()和getExp()得到,所谓的基元,就是不带指数的内容,当遍历到的Factor的基元在HashMap中,就将对应的值和指数相加进行合并,如果不在HashMap中,就新建一个基元和指数的键值对。
至于Expr中的合并同类项,需要修改原HashMap中的内容。由于项不再是简单的幂函数形式,项是否相等该如何判断呢?答案是重写每一个类的hashCode和equals方法。之后在Expr中建立一个HashMap套HashSet的结构(即HashMap<HashSet<Factor>, BigInteger>),键是merge之后的Term,值为Coefficient(也就是系数),合并同类项的方法也和第一次作业一样,遍历到的Term在HashMap中,就将系数和对应的值相加,如果该Term不在HashMap中,就新建一个键值对。
输出结果
由于项变复杂了,第一次作业中的简单处理不好用了,于是我在Expr、Term、Factor中构造了递归的toString()方法,实现了答案的输出。
性能优化
在第一次作业的基础上,还做了以下优化:
Trifunction中为0时,转为Number的0或1- 将
Trifunction里面的负号提到外面 - 由于当时时间不够
(这次是真的时间不够,不是懒癌犯了),就没有做\(sin(x)^2+cos(x)^2=1\)的化简
分析部分
类图分析

复杂度分析
| Class | OCavg | OCmax | WMC |
|---|---|---|---|
| Parser | 8.818181818181818 | 16.0 | 97.0 |
| MainClass | 5.0 | 5.0 | 5.0 |
| Lexer | 2.111111111111111 | 7.0 | 19.0 |
| expr.Trifunction | 1.8571428571428572 | 5.0 | 26.0 |
| expr.Totaldiyfunctions | 1.0 | 1.0 | 3.0 |
| expr.Term | 4.466666666666667 | 16.0 | 67.0 |
| expr.Sumfunction | 3.4 | 13.0 | 17.0 |
| expr.Pow | 1.2222222222222223 | 3.0 | 11.0 |
| expr.Number | 1.2857142857142858 | 3.0 | 9.0 |
| expr.Exprpow | 1.0 | 1.0 | 6.0 |
| expr.Expr | 2.4615384615384617 | 9.0 | 32.0 |
| expr.Diyfunction | 2.2857142857142856 | 9.0 | 16.0 |
| Method | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
| Parser.trifactor(String) | 39.0 | 12.0 | 14.0 | 16.0 |
| Parser.sumfactor() | 14.0 | 1.0 | 13.0 | 13.0 |
| Parser.removed(String, Number, int) | 2.0 | 2.0 | 2.0 | 2.0 |
| Parser.powfactor(String) | 14.0 | 4.0 | 7.0 | 7.0 |
| Parser.parseTerm() | 28.0 | 3.0 | 14.0 | 15.0 |
| Parser.Parser(Lexer) | 0.0 | 1.0 | 1.0 | 1.0 |
| Parser.parseFactor() | 9.0 | 6.0 | 12.0 | 12.0 |
| Parser.parseExpr() | 24.0 | 4.0 | 15.0 | 15.0 |
| Parser.numfactor() | 4.0 | 4.0 | 4.0 | 4.0 |
| Parser.exprfactor() | 15.0 | 5.0 | 8.0 | 8.0 |
| Parser.diyfactor(String) | 14.0 | 4.0 | 10.0 | 10.0 |
| MainClass.main(String[]) | 7.0 | 1.0 | 5.0 | 5.0 |
| Lexer.setTotaldiyfunctions(Totaldiyfunctions) | 0.0 | 1.0 | 1.0 | 1.0 |
| Lexer.peek() | 0.0 | 1.0 | 1.0 | 1.0 |
| Lexer.next() | 8.0 | 2.0 | 6.0 | 9.0 |
| Lexer.Lexer(String) | 0.0 | 1.0 | 1.0 | 1.0 |
| Lexer.getWhite() | 3.0 | 1.0 | 3.0 | 4.0 |
| Lexer.getTotaldiyfunctions() | 0.0 | 1.0 | 1.0 | 1.0 |
| Lexer.getNumber() | 2.0 | 1.0 | 3.0 | 3.0 |
| Lexer.getMult() | 2.0 | 1.0 | 3.0 | 3.0 |
| Lexer.getFunction() | 2.0 | 1.0 | 3.0 | 3.0 |
| expr.Trifunction.Trifunction(String, int, Factor) | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Trifunction.toString() | 5.0 | 1.0 | 5.0 | 5.0 |
| expr.Trifunction.substitute(String, Factor) | 7.0 | 1.0 | 5.0 | 5.0 |
| expr.Trifunction.substitute(BigInteger) | 3.0 | 1.0 | 3.0 | 3.0 |
| expr.Trifunction.setExponent(int) | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Trifunction.setContent(Factor) | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Trifunction.hashCode() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Trifunction.getRadix() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Trifunction.getName() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Trifunction.getExponent() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Trifunction.getExp() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Trifunction.getContent() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Trifunction.equals(Object) | 4.0 | 3.0 | 4.0 | 6.0 |
| expr.Trifunction.copy() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Totaldiyfunctions.Totaldiyfunctions() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Totaldiyfunctions.getDiyfunctions() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Totaldiyfunctions.addFunction(Diyfunction) | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Term.toString() | 21.0 | 1.0 | 12.0 | 12.0 |
| expr.Term.Term() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Term.substitute(String, Factor) | 40.0 | 1.0 | 16.0 | 16.0 |
| expr.Term.substitute(BigInteger) | 28.0 | 1.0 | 13.0 | 13.0 |
| expr.Term.setSimplified(boolean) | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Term.multsimplify() | 7.0 | 1.0 | 4.0 | 4.0 |
| expr.Term.merge() | 18.0 | 1.0 | 9.0 | 9.0 |
| expr.Term.isSimplified() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Term.hashCode() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Term.getFactors() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Term.getCoefficient() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Term.equals(Object) | 4.0 | 3.0 | 3.0 | 5.0 |
| expr.Term.copy() | 1.0 | 1.0 | 2.0 | 2.0 |
| expr.Term.addFactor(Factor) | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Term.addAllFactor(ArrayList) | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Sumfunction.Sumfunction(BigInteger, BigInteger, Factor) | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Sumfunction.simplify() | 29.0 | 1.0 | 12.0 | 13.0 |
| expr.Sumfunction.getRadix() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Sumfunction.getExp() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Sumfunction.copy() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Pow.setName(String) | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Pow.Pow(String, int) | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Pow.hashCode() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Pow.getRadix() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Pow.getName() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Pow.getExponent() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Pow.getExp() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Pow.equals(Object) | 4.0 | 3.0 | 3.0 | 5.0 |
| expr.Pow.copy() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Number.Number(BigInteger) | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Number.hashCode() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Number.getRadix() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Number.getNum() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Number.getExp() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Number.equals(Object) | 3.0 | 3.0 | 2.0 | 4.0 |
| expr.Number.copy() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Exprpow.getRadix() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Exprpow.getFactor() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Exprpow.getExponent() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Exprpow.getExp() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Exprpow.Exprpow(Factor, int) | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Exprpow.copy() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Expr.toString() | 8.0 | 1.0 | 5.0 | 5.0 |
| expr.Expr.substitute(String, Factor) | 1.0 | 1.0 | 2.0 | 2.0 |
| expr.Expr.substitute(BigInteger) | 1.0 | 1.0 | 2.0 | 2.0 |
| expr.Expr.mult(Expr) | 4.0 | 1.0 | 4.0 | 4.0 |
| expr.Expr.hashCode() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Expr.getTerms() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Expr.getRadix() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Expr.getExp() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Expr.Expr() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Expr.equals(Object) | 3.0 | 3.0 | 2.0 | 4.0 |
| expr.Expr.copy() | 1.0 | 1.0 | 2.0 | 2.0 |
| expr.Expr.addTerm(Term) | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Expr.addsimplify() | 22.0 | 4.0 | 8.0 | 9.0 |
| expr.Diyfunction.simplify(Totaldiyfunctions) | 24.0 | 3.0 | 9.0 | 9.0 |
| expr.Diyfunction.setContent(Expr) | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Diyfunction.getRadix() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Diyfunction.getExp() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Diyfunction.Diyfunction(String) | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Diyfunction.copy() | 1.0 | 1.0 | 2.0 | 2.0 |
| expr.Diyfunction.addArgument(Factor) | 0.0 | 1.0 | 1.0 | 1.0 |
第二次作业复杂度较高的几个地方主要是新加入的三种函数的部分,由于要使用递归替换,而且为了性能,替换中总要特判几下(比如处理sin(0)和sin(-1)之类的数据),并且,这三个函数的加入加重了Parser的复杂度,原因是我在Parser中就要将新加入的三种函数化简了,这也是架构带来的硬伤。之后就是Term的toString方法了,原因是不同因子输出的格式有所不同,且为了性能得加入很多特判。(虽然也有我代码水平的问题了)总体来说,由于第二次作业花的时间少,导致复杂度非常高,可以说是是三次作业中最丑的了。
测试部分
自测
- 在第一作业的评测机上进行了修改,由于
python的sympy会对三角函数进行化简,所以不能使用字符串对比的方法来验证是否正确,而是改为将100个数代入后对比得到的结果是否一样。 - 手造了几组较小的数据进行测试,比如
0,sin(x),1-1之类的 - 值得一提的是,评测机生成了一个答案约为72.7k的数据,我们整个宿舍都觉得这个数据非常强,就把它奉为检验的最强防线,这个数据甚至沿用到了第三次作业
互测
公测和互测中被Hack了一个点,该点的bug是由于手误,if...else...结构中少写了三行的else...内容,能暴露这个bug的只能是非常限定的小数据。这件事也告诉我,不能过度依靠评测机,评测机虽然能生成非常复杂的数据来检测,但还需自己构造那些非常限定的小数据。同时,我还在房间中成功找出了别人的1个bug,该bug是由于该同学对于\(sin(-1)^2\)等数据中,将-直接提到外面,不考虑指数。除了WA掉一个点外,由于没有做\(sin(x)^2+cos(x)^2=1\)的化简,导致性能分也丢了5分。(属实是屋漏偏逢连夜雨了)
第三次作业
代码部分
架构分析
相比于第二次作业,第三次作业基本上没有什么新东西的加入,我只做了一些代码的美化工作,比如把公共部分提出来成为新的方法。
解析输入
数据结构还是和第二次作业一样的五个部分,解析时遇到三种函数也是当场就进行化简。
数学化简
相比于第二次作业,实现了绝大多数情况下\(sin(x)^2+cos(x)^2=1\)的化简。具体方法是,遍历地将\(sin(Factor)^k\times Term(k\ge2)\)替换为\((1-cos(Factor.simplify())^2)\times sin(Factor.simplify())^{k-2}\times Term\),将\(sin(Factor)^k\times Term(k\lt2)\)替换为$ sin(Factor.simplify())^k\times Term$,如果替换并化简后的表达式长度比原来的要更短,就输出更短的那个结果。同理,还有将cos化为sin的版本,将这三个版本的结果长度进行比较,输出最短的。这种方法虽然无法覆盖所有的情况,但它比较简单,且效果显著。
其次,由于本次作业中Trifunction中可以是Expr了,为了丢掉多余的括号,在Trifunction的化简部分要加入一些判断,判断Expr中是否只有一个Term,且该Term中只有一个Factor,如果是这样的话,就可以直接拆包将里面的Factor拆出来。
最后,如果Trifunction中的Expr里全是负项,就可以提出一个负号。那如何得知Expr里全是负项呢?我想到了一个简单的办法就是直接判断Expr.toString()是不是负号打头。原理就是,Expr.toString()方法中,会尽可能地让正项放在前面,如果第一项都为负了,那么整个Expr中的项都是负的,也就可以把公共的负号提出来了,具体提出的方法和第二次作业一样,sin需要考虑指数,cos直接丢掉就好。当然,在对里面的Expr做Expr.toString()的方法进行判断前,需要对其使用Expr.addsimplify()方法进行化简,这也就形成了一个递归的过程,使得类似于sin(sin(sin(-1)))的数据能将最里面的负号提到最外面。
输出结果
本次作业的输出与第二次作业的差别不大,唯一要注意的点是Trifunction中,如果为Expr需要加括号,其他情况则不需要(这也就是上述化简中需要尽可能拆包的原因)。
性能优化
在第二次作业的基础上,还做了以下优化:
- 将
Trifunction里面的负号提到外面(这次需要考虑内部为Expr和嵌套的情况) - \(sin(x)^2+cos(x)^2=1\)的化简
分析部分
类图分析

复杂度分析
| Class | OCavg | OCmax | WMC |
|---|---|---|---|
| Parser | 6.0 | 18.0 | 72.0 |
| MainClass | 7.0 | 7.0 | 7.0 |
| Lexer | 2.111111111111111 | 7.0 | 19.0 |
| expr.Trifunction | 2.6875 | 7.0 | 43.0 |
| expr.Totaldiyfunctions | 1.0 | 1.0 | 3.0 |
| expr.Term | 4.176470588235294 | 14.0 | 71.0 |
| expr.Sumfunction | 3.2 | 12.0 | 16.0 |
| expr.Pow | 1.25 | 3.0 | 10.0 |
| expr.Number | 1.2857142857142858 | 3.0 | 9.0 |
| expr.Exprpow | 1.1428571428571428 | 2.0 | 8.0 |
| expr.Expr | 3.0 | 12.0 | 45.0 |
| expr.Diyfunction | 2.2857142857142856 | 9.0 | 16.0 |
| Method | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
| Parser.trifactor(String) | 36.0 | 13.0 | 16.0 | 19.0 |
| Parser.sumfactor() | 6.0 | 1.0 | 5.0 | 5.0 |
| Parser.removed(String, Number, int) | 2.0 | 2.0 | 2.0 | 2.0 |
| Parser.removed(String, Expr, int) | 10.0 | 3.0 | 6.0 | 6.0 |
| Parser.powfactor(String) | 7.0 | 3.0 | 4.0 | 4.0 |
| Parser.parseTerm() | 18.0 | 1.0 | 10.0 | 10.0 |
| Parser.Parser(Lexer) | 0.0 | 1.0 | 1.0 | 1.0 |
| Parser.parseFactor() | 9.0 | 6.0 | 12.0 | 12.0 |
| Parser.parseExpr() | 10.0 | 4.0 | 8.0 | 8.0 |
| Parser.numfactor() | 3.0 | 3.0 | 3.0 | 3.0 |
| Parser.exprfactor() | 8.0 | 4.0 | 5.0 | 5.0 |
| Parser.diyfactor(String) | 5.0 | 4.0 | 5.0 | 5.0 |
| MainClass.main(String[]) | 11.0 | 1.0 | 8.0 | 8.0 |
| Lexer.setTotaldiyfunctions(Totaldiyfunctions) | 0.0 | 1.0 | 1.0 | 1.0 |
| Lexer.peek() | 0.0 | 1.0 | 1.0 | 1.0 |
| Lexer.next() | 8.0 | 2.0 | 6.0 | 9.0 |
| Lexer.Lexer(String) | 0.0 | 1.0 | 1.0 | 1.0 |
| Lexer.getWhite() | 3.0 | 1.0 | 3.0 | 4.0 |
| Lexer.getTotaldiyfunctions() | 0.0 | 1.0 | 1.0 | 1.0 |
| Lexer.getNumber() | 2.0 | 1.0 | 3.0 | 3.0 |
| Lexer.getMult() | 2.0 | 1.0 | 3.0 | 3.0 |
| Lexer.getFunction() | 2.0 | 1.0 | 3.0 | 3.0 |
| expr.Trifunction.Trifunction(String, int, Factor) | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Trifunction.toString() | 7.0 | 1.0 | 7.0 | 7.0 |
| expr.Trifunction.substitute(String, Factor) | 5.0 | 1.0 | 5.0 | 5.0 |
| expr.Trifunction.substitute(BigInteger) | 5.0 | 1.0 | 5.0 | 5.0 |
| expr.Trifunction.sintocos() | 6.0 | 1.0 | 5.0 | 6.0 |
| expr.Trifunction.setContent(Factor) | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Trifunction.insidechange() | 11.0 | 1.0 | 9.0 | 9.0 |
| expr.Trifunction.hashCode() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Trifunction.getRadix() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Trifunction.getName() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Trifunction.getExponent() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Trifunction.getExp() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Trifunction.getContent() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Trifunction.equals(Object) | 4.0 | 3.0 | 4.0 | 6.0 |
| expr.Trifunction.costosin() | 6.0 | 1.0 | 5.0 | 6.0 |
| expr.Trifunction.copy() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Totaldiyfunctions.Totaldiyfunctions() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Totaldiyfunctions.getDiyfunctions() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Totaldiyfunctions.addFunction(Diyfunction) | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Term.toString() | 21.0 | 1.0 | 12.0 | 12.0 |
| expr.Term.Term() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Term.substitute(String, Factor) | 36.0 | 1.0 | 13.0 | 14.0 |
| expr.Term.substitute(BigInteger) | 27.0 | 1.0 | 12.0 | 12.0 |
| expr.Term.setSimplified(boolean) | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Term.removed(String, Number, int) | 2.0 | 2.0 | 2.0 | 2.0 |
| expr.Term.removed(String, Expr, int) | 10.0 | 3.0 | 6.0 | 6.0 |
| expr.Term.multsimplify() | 7.0 | 1.0 | 4.0 | 4.0 |
| expr.Term.merge() | 18.0 | 1.0 | 9.0 | 9.0 |
| expr.Term.isSimplified() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Term.hashCode() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Term.getFactors() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Term.getCoefficient() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Term.equals(Object) | 4.0 | 3.0 | 3.0 | 5.0 |
| expr.Term.copy() | 1.0 | 1.0 | 2.0 | 2.0 |
| expr.Term.addFactor(Factor) | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Term.addAllFactor(ArrayList) | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Sumfunction.Sumfunction(BigInteger, BigInteger, Factor) | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Sumfunction.simplify() | 28.0 | 1.0 | 11.0 | 12.0 |
| expr.Sumfunction.getRadix() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Sumfunction.getExp() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Sumfunction.copy() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Pow.Pow(String, int) | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Pow.hashCode() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Pow.getRadix() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Pow.getName() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Pow.getExponent() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Pow.getExp() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Pow.equals(Object) | 4.0 | 3.0 | 3.0 | 5.0 |
| expr.Pow.copy() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Number.Number(BigInteger) | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Number.hashCode() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Number.getRadix() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Number.getNum() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Number.getExp() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Number.equals(Object) | 3.0 | 3.0 | 2.0 | 4.0 |
| expr.Number.copy() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Exprpow.getRadix() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Exprpow.getFactor() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Exprpow.getExponent() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Exprpow.getExp() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Exprpow.Exprpow(Factor, int) | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Exprpow.expand() | 1.0 | 1.0 | 2.0 | 2.0 |
| expr.Exprpow.copy() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Expr.toString() | 8.0 | 1.0 | 5.0 | 5.0 |
| expr.Expr.substitute(String, Factor) | 1.0 | 1.0 | 2.0 | 2.0 |
| expr.Expr.substitute(BigInteger) | 1.0 | 1.0 | 2.0 | 2.0 |
| expr.Expr.sintocos() | 8.0 | 1.0 | 7.0 | 7.0 |
| expr.Expr.mult(Expr) | 4.0 | 1.0 | 4.0 | 4.0 |
| expr.Expr.hashCode() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Expr.getTerms() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Expr.getRadix() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Expr.getExp() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Expr.Expr() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Expr.equals(Object) | 3.0 | 3.0 | 2.0 | 4.0 |
| expr.Expr.costosin() | 8.0 | 1.0 | 7.0 | 7.0 |
| expr.Expr.copy() | 1.0 | 1.0 | 2.0 | 2.0 |
| expr.Expr.addTerm(Term) | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Expr.addsimplify() | 29.0 | 4.0 | 11.0 | 12.0 |
| expr.Diyfunction.simplify(Totaldiyfunctions) | 24.0 | 3.0 | 9.0 | 9.0 |
| expr.Diyfunction.setContent(Expr) | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Diyfunction.getRadix() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Diyfunction.getExp() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Diyfunction.Diyfunction(String) | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Diyfunction.copy() | 1.0 | 1.0 | 2.0 | 2.0 |
| expr.Diyfunction.addArgument(Factor) | 0.0 | 1.0 | 1.0 | 1.0 |
虽然第三次作业的指标相较于第二次作业来说并没有下降,但是也没有出现新的红指标了。这样看来的话,新加入部分的耦合度还是比较好的。
测试部分
自测
和第二次作业的部分几乎一样。但有了第二次作业的教训,对小数据的构造更上心了。
互测
公测和互测中均未被Hack,但是由于未做二倍角化简等丢了3分性能分。但是在房间中成功找出了别人的9个bug(应该有7个不同质的)。这些bug分为这几种:
sum函数中,循环变量没有使用BigIntegersum函数中,使用字符串替换时,没有套括号,导致\(sum(i,-2,-1,i^2)\)算出来的结果为-5- 对于\(sin(-1)^2\)等数据中,将
-直接提到外面,不考虑指数 - 结果为0时,输出空串
- 结果为\(sin((-x))\)等数据中,输出的结果为\(sin(-x)\),没有输出必要的括号
- \(sin(0)^0\)输出0而不是1
心得体会
总的来说,第一单元让我懂得了很多。首先,它让我知道了我的思考总是不全面的,总是简单想完就开写,每次都会遇到致命缺陷的地方。第一次作业中,我一开始的思路的实现需要一边遍历ArrayList一边对其进行修改,这样就会造成遍历顺序出错,其次,由于使用分配律,导致算不了很复杂的式子,只能通过重构来解决,第二次作业中,由于需要使用递归替换,就必须实现拷贝的方法,而当时我并不会clone,只能写了个拷贝的方法加进去才能解决,第三次作业中,由于架构原因,每到关键步都得化简,使得代码重复部分较多,这些都是非常大的硬伤,而每次都要等到写到那个地方才能发现,且这些都不好解决,硬要解决还得从老远之前重写。其次,第一单元暴露了我两个缺点。首先是为了图方便而无所不用其极,导致代码破破烂烂,其次是为了优化性能而无所不用其极,导致代码处处臃肿,甚至还有专门外挂的方法来对输出进行优化。
但不得不说,我确实感觉自己提高了很多。首先是有了一次写大工程代码的经验,让我有机会去思考如何构造大工程的代码,并合理地布局,让代码看起来思路清晰。其次,由于三次作业是递进关系,也让我收获了如何让自己的代码可迭代性更强的技巧。在知识层面上,我收获了面向对象编程的技巧,以及一些类似于递归下降,重写hashCode的方法之类的技能和技巧。同时,我也收获了成功的喜悦,在做第一次作业之前,我从来没有做大工程的经历,当看到题目后我甚至一点思路都没有,看完训练栏目后,都处于懵逼的状态,后来还是艰难地开了头,之后越写思路越清晰,到最后发现自己成功完成后还觉得很不可思议,“嘿,我还真就做出来了!”那次让我整整开心了三天。但是之后第二次作业由于时间太紧了,加上WA了一个点,心里甚至都有点不好受。第三次作业,由于加的东西太少了,没啥感觉。同时,我心境上也更加成熟了,知道万事开头难,坚持下去就一定能做出来,知道了花的时间越多,回报就越大,知道了有些东西不能去盲目追求了。
最后,虽然第二次作业时由于花费时间较少而WA了一个点,稍微有点遗憾之外,第一单元还是结束了,希望我第二单元能够做得更好吧。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号