圆的排列问题

问题

给定n个圆的半径序列，将它们放到矩形框中，各圆与矩形底边相切，求具有最小排列长度的圆排列。

解析

利用回溯法。计算当前遍历到的圆，与前面已经排列好的圆相切之后的圆心坐标，这个地方要注意一点，并不是一定和第i-1个圆相切，比如

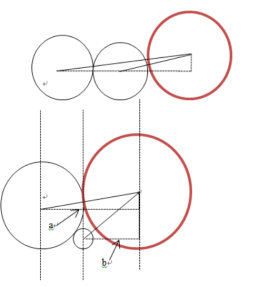
所以要从头遍历1-i，找出最大的x坐标，即为此圆的圆心坐标。

根据回溯的基本思想，当遍历到的圆等于总数n时，即表示已经完成了一组排列，此时可以计算这种情况下的长度，再接着回溯。在不断的回溯完成排列中，不断更新最小值ans（还可以顺便更新记录此时的排列情况，在最后输出），最短长度即为ans。

①. 在计算圆心坐标时，采用化简，x^2 = sqrt((r1+r2)^2-(r1-r2)^2)  =>  x = 2 * sqrt(r1 * r2)

②. 在计算长度时，遍历找到最左端和最右端的坐标，相减即是此时的长度。

 

设计

double get(int x){//计算圆心坐标
　　double cnt=0.0;
　　for(int i=1;i<x;i++){
    　　cnt=max(cnt,p[i]+2.0*sqrt(r[x]*r[i]));
　　}
    return cnt;
}
void solve(int c){
    if(c==n){//如果遍历到的圆的数目等于n，则表示已经搜索到了叶节点，排列完成。
        计算此时的长度;
        return;
    }
    for(int i=x;i<=n;i++){
        swap(r[x],r[i]);
        if(满足条件){
            搜索下一个点;
        }
        swap(r[x],r[i]);//回溯
    }      
}

分析

最坏情况下的排列树需要n!此计算，每次计算需要O(n)，所以总的复杂度为O((n+1)!)。

源码

/*
author: keke
project name:圆排列问题
Time Complexity: O((n+1)!)
*/
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define db double
const int maxn = 110;
int n;
db r[maxn], ans = 1e9, p[maxn],ans1[maxn];
db com() {
    db l=0.0,h=0.0;
    for(int i=1;i<=n;i++){
        l=min(l,p[i]-r[i]);
        h=max(h,p[i]+r[i]);
    }
    if(ans>h-l){
        ans=h-l;
        for(int i=1;i<=n;i++)ans1[i]=r[i];
    }
}
db get(int x) {
    db sum = 0.0;
    for (int i = 1; i < x; i++)sum = max(sum, p[i] + 2.0 * sqrt(r[i] * r[x]));
    return sum;
}
void solve(int x) {
    if (x > n) {
        com();
        return;
    }
    for (int i = x; i <= n; i++) {
        swap(r[x], r[i]);
        db cnt = get(x);
        if (cnt + r[1] + r[x] < ans) {
            //圆排列的圆心横坐标以第一个圆的圆心为原点。
            //所以，总长度为第一个圆的半径+最后一个圆的半径+最后一个圆的横坐标。
            p[x] = cnt;
            solve(x + 1);
        }
        swap(r[x], r[i]);//回溯
    }
}
int main() {
    ios::sync_with_stdio(false);
    cout << fixed << setprecision(2);
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> r[i];
    solve(1);
    cout << "最短长度为" << ans << "\n";
    cout << "最优情况下，圆的半径依次为";
    for (int i = 1; i <= n; i++) cout << ans1[i] << (i == n ? "\n" : " ");
    return 0;
    // good job!
}