LCS算法

1. 问题

两个串a和b，求最长的、公共的、子序列的长度。

比如a={1,2,3,4,5},b={3,2,1,4,5};

那么很明显lcs的长度为3，这个串是{3,4,5}，这个公共子串不唯一。

 

2. 解析

很容易想到一个动态规划做法，dp[i][j]表示，a的前i位，b的前j位的lcs。

 

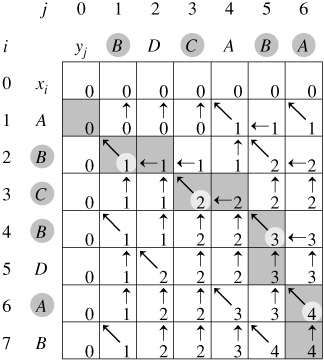
3. 设计

状态转移方程：

if(a[i]==b[j])dp[i][j]=max(dp[i][j],dp[i-1][j-1]+1);//当前两个字符一样

else dp[i][j]=max(dp[i-1][j],dp[i-1][j]);

在转移前，要将dp[i][0]和dp[0][j]初始化为0。

 

4. 分析

dp过程中，套了两层for，分别为1->n，1->m，所有时间复杂度为O(NM)。

 

5. 源码

/*
author: keke
project name:LCS算法 
Time Complexity: O(nm)
*/
#include<iostream>
using namespace std;
int dp[1001][1001],a1[2001],a2[2001],n,m;
int main() {
    //dp[i][j]表示两个串从头开始，直到第一个串的第i位
    //和第二个串的第j位最多有多少个公共子元素
    cin>>n>>m;
    for(int i=1; i<=n; i++)cin>>a1[i],dp[i][0]=0;
    for(int i=1; i<=m; i++)cin>>a2[i],dp[0][i]=0;
    for(int i=1; i<=n; i++) {
        for(int j=1; j<=m; j++) {
            if(a1[i]==a2[j])dp[i][j]=max(dp[i][j],dp[i-1][j-1]+1);
            else dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
        }
    }
    cout<<dp[n][m];
}