投资问题（动态规划）

1. 问题

设m元钱，n项投资，函数fi(x)表示将x元投入第i项项目所产生的效益，i=1,2,...,n.

问：如何分配这m元钱，使得投资的总效益最高？

 

2. 解析

 　　

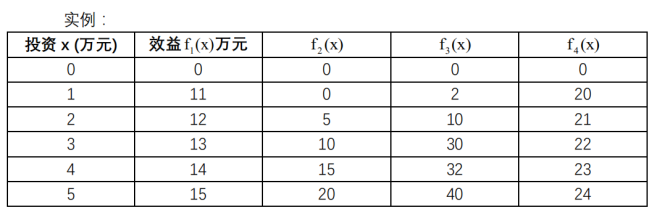
　　我们维护一个二维数组dp，dp[i][j]表示前i个项目投资j元钱的最大效益，使用动态规划时，考虑如何将问题划分成子问题，我们可以先从第一个项目考虑，然后考虑前两个项目，然后前三个项目，到第m个项目时，为m分配x元钱，n-x元钱的最大效益为dp[m-1][n-x]，这样我们可以得到递推方程：

　　dp[x][y]=max{f（x，i）+dp[x-1][y-i]}（i的取值[0，y]）

 

3. 设计

for (int i = 1; i <= n; i++) {
        for (int j = 0; j <= money; j++) {
            dp[i][j] = 0;
            for (int k = 0; k <= j; k++) {
                if (dp[i][j] < f[i][k] + dp[i - 1][j - k])
                    dp[i][j] = f[i][k] + dp[i - 1][j - k];
         　　}
        }
}

 

4. 分析

 

 

 

5. 源码

#include <iostream>
#include <math.h>
using namespace std;
const int M = 5;
const int N = 6;
int MaxProfit(int dp[M][N],int f[M][N],int n,int money) {
    for (int i = 1; i <= n; i++) {
        for (int j = 0; j <= money; j++) {
            dp[i][j] = 0;
            for (int k = 0; k <= j; k++) {
                if (dp[i][j] < f[i][k] + dp[i - 1][j - k])
                    dp[i][j] = f[i][k] + dp[i - 1][j - k];
            }
        }
    }
    return dp[n][money];
}
int main() {
    int dp[M][N] = { 0 };
    int f[M][N] = { 0,0,0,0,0,0,
                    0,11,12,13,14,15,
                    0,0,5,10,15,20,
                    0,2,10,30,32,40,
                    0,20,21,22,23,24
                  };
    cout << MaxProfit(dp, f, 4, 5);
    return 0;
}