归并排序

1. 问题

　　归并排序（MERGE-SORT）是利用归并的思想实现的排序方法，该算法采用经典的分治（divide-and-conquer）策略（分治法将问题分(divide)成一些小的问题然后递归求解，而治(conquer)的阶段则将分的阶段得到的各答案"修补"在一起，即分而治之)。

 

2. 解析

　　

 

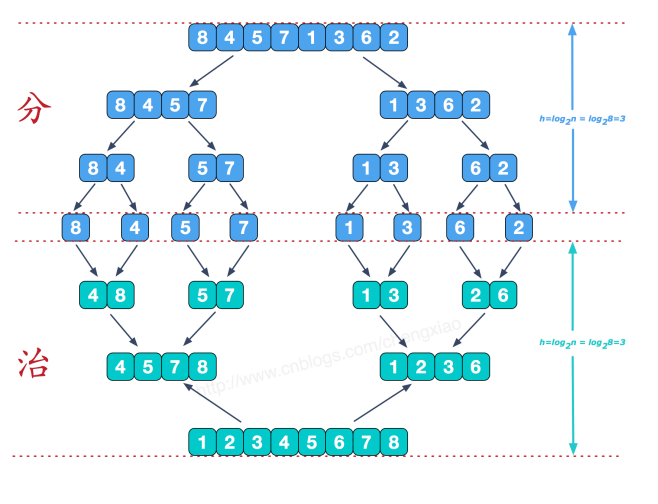
　　可以看到这种结构很像一棵完全二叉树，我们采用递归去实现（也可采用迭代的方式去实现）。分阶段可以理解为就是递归拆分子序列的过程，递归深度为log2n。

-------------------------------------------------------------------------------------------------------------------------------------

　　

 

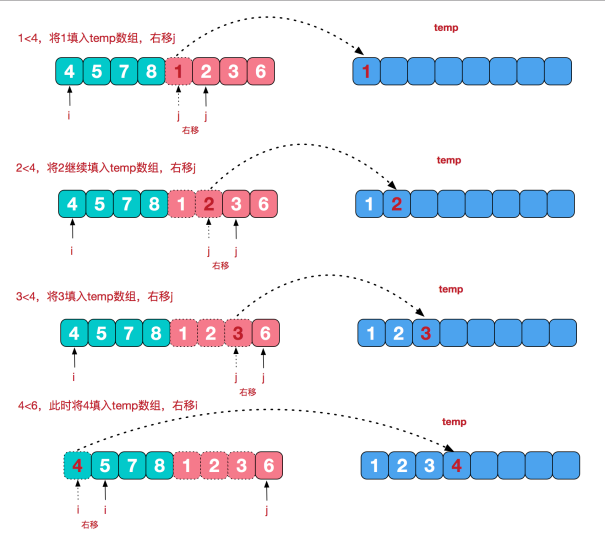
　　　再来看看治阶段，我们需要将两个已经有序的子序列合并成一个有序序列，比如上图中的最后一次合并，要将[4,5,7,8]和[1,2,3,6]两个已经有序的子序列，合并为最终序列[1,2,3,4,5,6,7,8]，来看下实现步骤。

 

3. 设计

void solve(int low,int high){
    if(low>=high)return;
    int temp[maxn];
    int mid=(low+high)>>1,l1=low,r1=mid+1,k=low;
　　//分
    solve(low,mid);
    solve(mid+1,high);
　　//治
    while(l1<=mid&&r1<=high){
        if(p[l1]>p[r1])sumac8+=mid-l1+1,temp[k++]=p[r1++];
        else temp[k++]=p[l1++];
    }
    while(l1<=mid)temp[k++]=p[l1++];
    while(r1<=high)temp[k++]=p[r1++];
    for(int i=low;i<=high;i++)p[i]=temp[i];
}

 

4. 分析

　　从上文的图中可看出，每次合并操作的平均时间复杂度为O(n)，而完全二叉树的深度为|log2n|。总的平均时间复杂度为O(nlogn)。

 

5.源码

　　

/*
author: keke
project name:二分归并排序算法
Time Complexity: O(nlogn)
*/
#include<stdio.h>
using namespace std;
int a[100001],temp[100001];
void bin(int l,int r){
    if(l==r) return ;
    int mid=(l+r)>>1;
    bin(l,mid);
    bin(mid+1,r);
    int i=l,j=mid+1,k=l;
    while(i<=mid && j<=r){
        if(a[i]<=a[j])temp[k++]=a[i++];
        else temp[k++]=a[j++];
    }
    while(i<=mid)temp[k++]=a[i++];
    while(j<=r)temp[k++]=a[j++];
    for(int i=l;i<=r;++i)a[i]=temp[i];
}
int main(){
    int n;
    scanf("%d",&n);
    for(int i=1;i<=n;++i)scanf("%d",&a[i]);
    bin(1,n);
    for(int i=1;i<=n;++i)printf("%d ",a[i]);
    return 0;
}