计数题目选做

AT_agc040_c Neither AB nor BA

题目大意：

一个由 \(ABC\) 构成的串是好的，当且仅当可以通过不删 \(AB\) 和 \(BA\) 的相邻的两个字符把它删空。
现在给定 \(n\)，求长度为 \(n\) 的字符串有多少是好的。
\(n \le 10^7,2 | n\)。

解题思路：

首先注意到 \(C\) 这个字符是没有施加任何限制的，所以可以看成任意填 \(A/B\)。
那么现在变成了如何判定一个 \(AB\) 串是否合法。
因为 \(AA\) 和 \(BB\) 形的 删除可能导致了 \(ABABABABAB\) 这种数量很多但不能删的情况。
也就是这样刻画会非常复杂。

但注意到因为是一次删两个，所以奇偶性永远不会变。
这样我们就找到了永恒的东西。

然后套套路，将偶数位置的 \(A/B\) 切换，那么一次就是删一个 \(AB/BA\) 了。
这样就很好了啊，因为只要 \(A,B\) 同时有，就一定会相交。

相交就意味着一定可以删除。
所以现在的问题就变为了 \(AB\) 不能有绝对众数，\(C\) 这时候就是用来平衡的了。

因为不能有绝对众数，而绝对众数只能有一个，所以简单容斥一下就好了。
\(O(n)\)。

AT_agc020_f Arcs on a Circle

题目大意：

你有 \(n\) 个线段，每个线段长度给定，现在在一个环上，每个线段的初始坐标在实数范围内随机，求覆盖整个环的概率。
\(n \le 6, L \le 50\)。

解题思路：

遇到小数部分，直接套路地枚举大小关系，然后这个题直接状压就行了。
\(O(2^n \times n! \times n^2 \times L^2)\)

AT_agc019_f Yes or No

题目大意：

已知一套试卷中有 \(N\) 个选 \(A\)，\(M\) 个选 \(B\)，你知道，需要逐一蒙 \(N+M\) 个题，而且你每蒙完一个就会给出这个题的答案。
而且答案在一开始就随机定了，问你期望答对多少题。
\(N,M \le 5 \times 10^5\)

解题思路：

首先我们肯定是要知道我们要怎么填这个答案，策略显然是填剩下多的那个。
于是我们就有一个网格图，往左走表示选 \(Yes\)，往右走表示选 \(No\)，由于 \(N,M\) 是对称的，所以不妨设 \(N > M\)。
所以我们的最优策略就会如下图红线一样（蓝线代表斜对角）

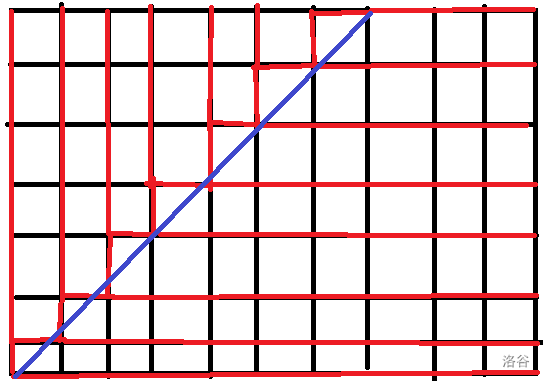
我们现在就是要求的每一条路径于红线交的期望数量。
考虑这个折线中横着的太难看了，而把他们去掉之后正好是一层一层的。
所以就是单独算这些的贡献然后加 \(N\)。
\(O(n)\)。