首先，0-1背包问题描述：
给你一个可装载最大重量为maxWeight的背包和N个物品，每个物品有重量(w)和价值(v)两个属性。
其中第i个物品的重量为w[i]，价值为v[i]，现在问，这个背包能装的最大价值是多少？
然后，我们按照题目假设如下：
//重量数组
int[] ws = new int[]{1,2,3,4,5};
//价值数组
int[] vs = new int[]{2,4,5,5,6};
求maxWeight=11时，最大价值，及其对应的物品序列。
那么，具体的极值填充过程如下：
如果背包最大承重为：[1,2,3,4,5,6,7,8,9,10,11]，那么对应的最大价值及其相应的物品填充序列，如下图：
横坐标（土色底色）从0到11，代表背包最大承重；
纵坐标（绿色底色）从0到5，代表重量数组；
纵坐标（蓝色底色）{0,2,4,5,5,6}代表重量对应的价值；
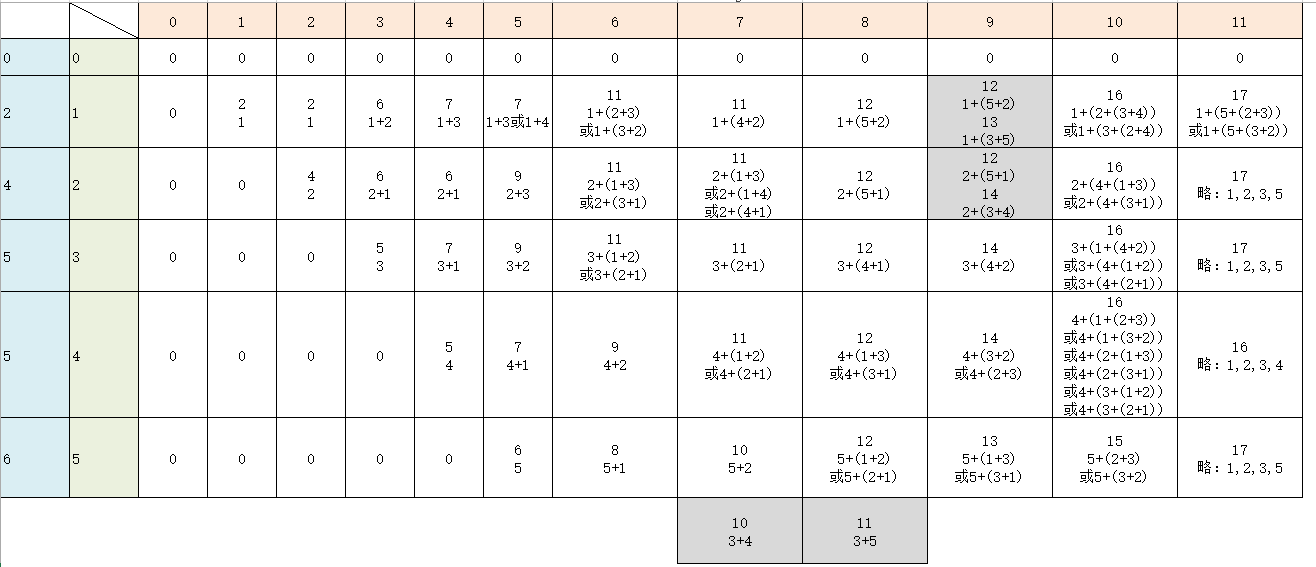
图解：
图中，如：
的含义为：最大承重为6的包，包内放置物品1的话，最大价值为11，其包含的物品为1,2,3共3件物品。
整个表格的所有白底色单元都上上述含义。其计算过程遵循如下规则：
想要知道最大承重为6的包，包内如果放置了物品1，那么其最大价值为：
物品1的价值（2） +
（最大承重为（6-1）= 5 的这一列里， 不包含物品1的，物品组合的价值的，最大值）
很好理解对吧。典型的递归对吧。
按照这个计算过程，能计算出所有白底单元的值，则，最终可以得到任意最大承重的包的，最大价值及其对应的物品组合。
另外，
灰色底色的特例，是因为在计算9列时，发现用这个计算方法无法计算出包内含1、含2的最大值，
但由于在计算含3、含5时，把上述遗漏的情况又包含了，所以其实没有最大价值及其物品组合，只是没法在第一时间找出，
只能在所有物品计算完毕后才能获得。这一点不影响计算的正确性。
这样，0-1背包问题，其实质，是基于一个二维数组，或者说二维坐标系的，极值填充选择问题。即如图：
设Y轴为 “放入重量为 y 的物品”，设X轴为 “限定总重量为 x ”，那么通过不断地填充极值，最终会形成一个，形如如下图的极值柱状图：
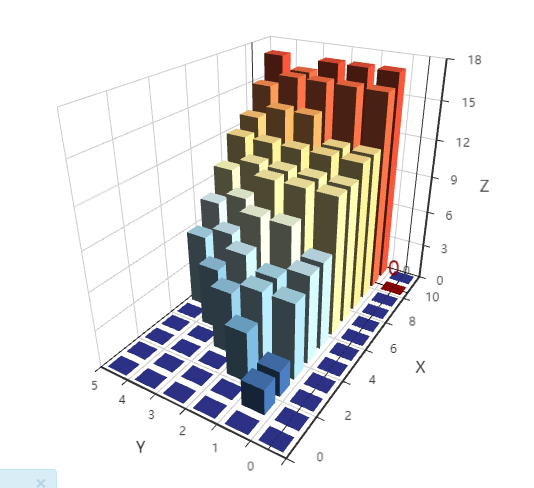
本文是用表格和图形的方式，对0-1背包问题进行了拆分式理解，
如果需要具体的代码，可以参照 labuladong 的0-1背包问题的代码。
