算法浅谈:插入-标记-查找
前言
lxl 的课属实让我受益匪浅,这篇博客就来谈一谈他自创的算法:插入-标记-查找
算法概述
这是一个离线算法,用到了扫描线思想和数据结构,它可以秒掉这样一类问题:
- 给定 \(n\) 个映射 \(f_i(x)\;(i \in [1,n])\) 和 \(m\) 个询问
- 每个询问形如给定 \(x,l,r\) 求 \(f_r(f_{r-1}(\dots f_{l+2}(f_{l+1}(f_l(x)))\dots))\),也就是以 \(x\) 为初值,从 \(l\) 到 \(r\) 依次对当前值做一次映射,求最后的值。
这个算法的优点是代码简单,面对不同的题目时核心代码(除了数据结构部分)都差不多,赛场上容易写出来。
但是这个算法也有缺点,首先,它不能解决在线问题,而且他虽然能秒题,但不一定是最优解(有时会多一个 \(\text{log}\)),导致容易被他的发明者卡常。
算法思路
首先我们知道几乎所有数据结构都可以全局做某个操作,那么我们考虑对于所有 \(i\;(i\in[1,n])\),所以我们可以把需要做 \(f_i\) 这个映射的询问统一处理,这样就只需要 \(O(n)\times O(\text{数据结构全局操作})\) 的时间就可以解决问题。
算法流程
对于一组询问,我们先对左端点排序,然后开始从左往右扫描线,对于扫到的每个位置 \(i\),我们做如下操作:
- 如果当前点是一个询问的 \(l\),那么把它对应的 \(x\) 放入数据结构;
- 将数据结构进行全局 \(f_i\) 映射;
- 如果当前点是一个询问的 \(r\),那么就把这个问题的答案赋值为这个问题插入时对应的那个节点的当前值。
如果你觉得上面的东西有些难懂,不妨看看下面的图解。
算法图解
我们设 \(f_i(x)=x+i\)(当然这个映射根本不需要这个算法,这里只是演示用),两个询问分别为 \((0,3,-5),(2,5,4)\)。
则初始时如下图(下面的方框代表数据结构,这里数据结构的内部修改就不演示了,这不是重点)
然后扫描线扫到 \(0\),我们发现这个位置是第 \(1\) 个询问的左端点,所以将对应的 \(-5\) 加入数据结构,然后全局加 \(0\),于是变成这个样子:
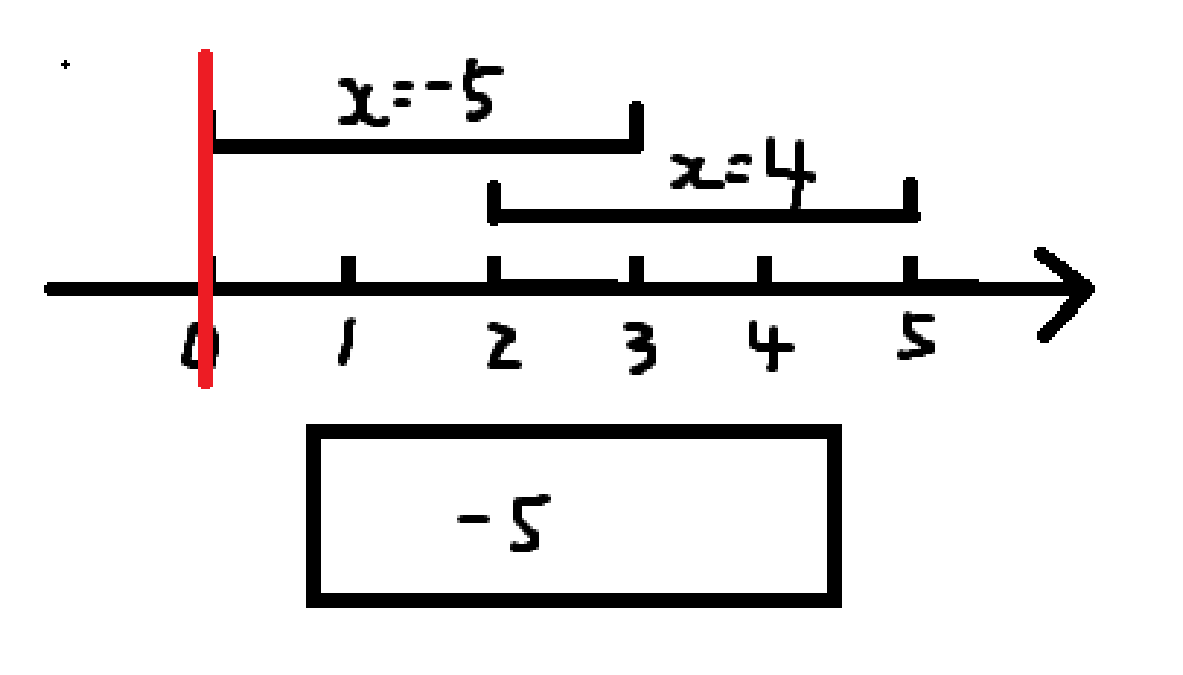
然后扫描线扫到 \(1\),全局加 \(1\),于是变成这个样子:
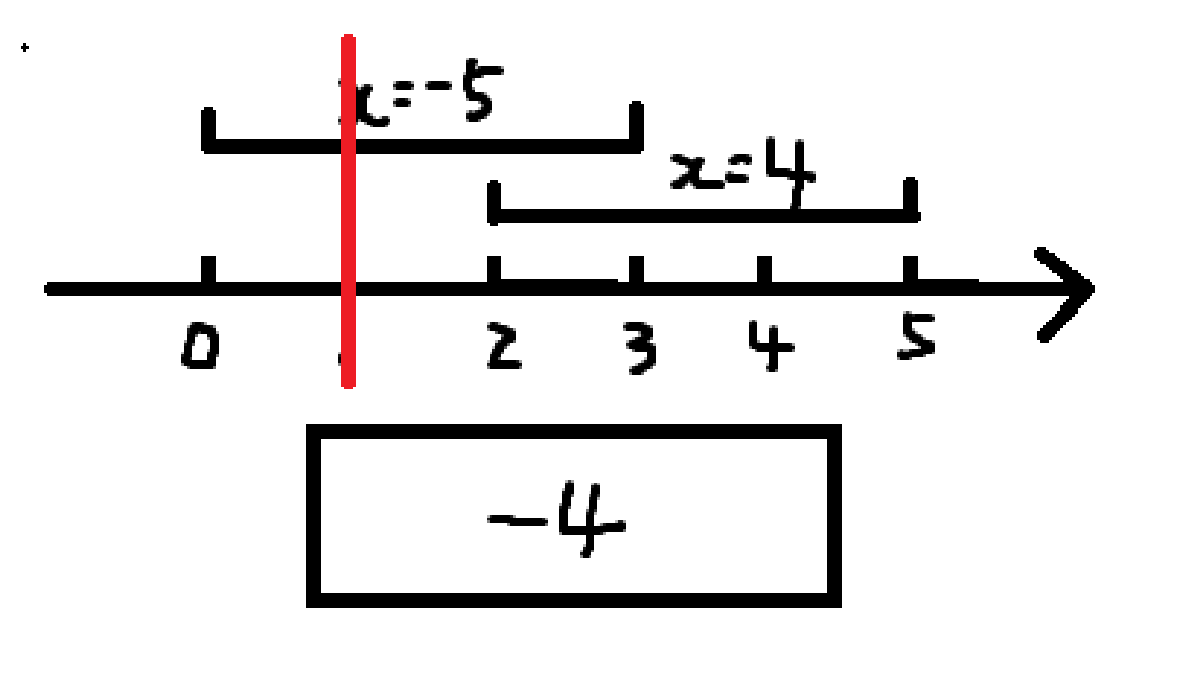
然后扫描线扫到 \(2\),我们发现这个位置是第 \(2\) 个询问的左端点,所以将对应的 \(4\) 加入数据结构,然后全局加 \(2\),于是变成这个样子:
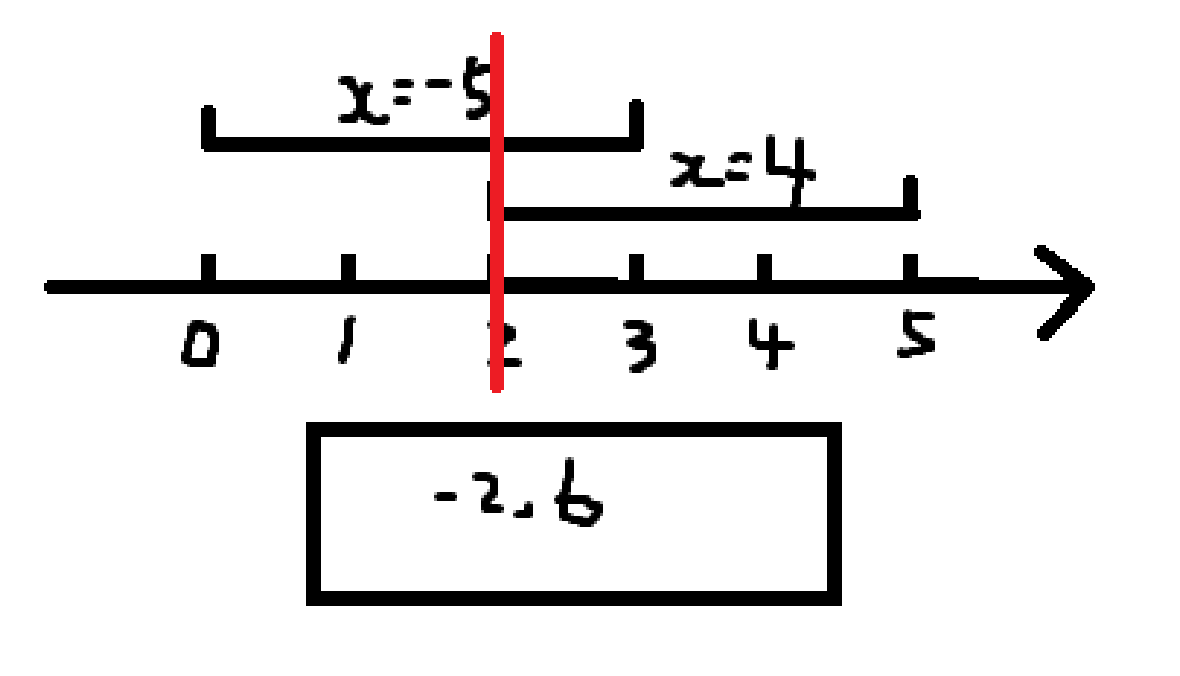
然后扫描线扫到 \(3\),全局加 \(3\),我们发现这个位置是第 \(1\) 个询问的右端点,所以第 \(1\) 个询问的答案就是 \(1\)(左端点在全局修改之前判,右端点在全局修改之后判),于是变成这个样子:
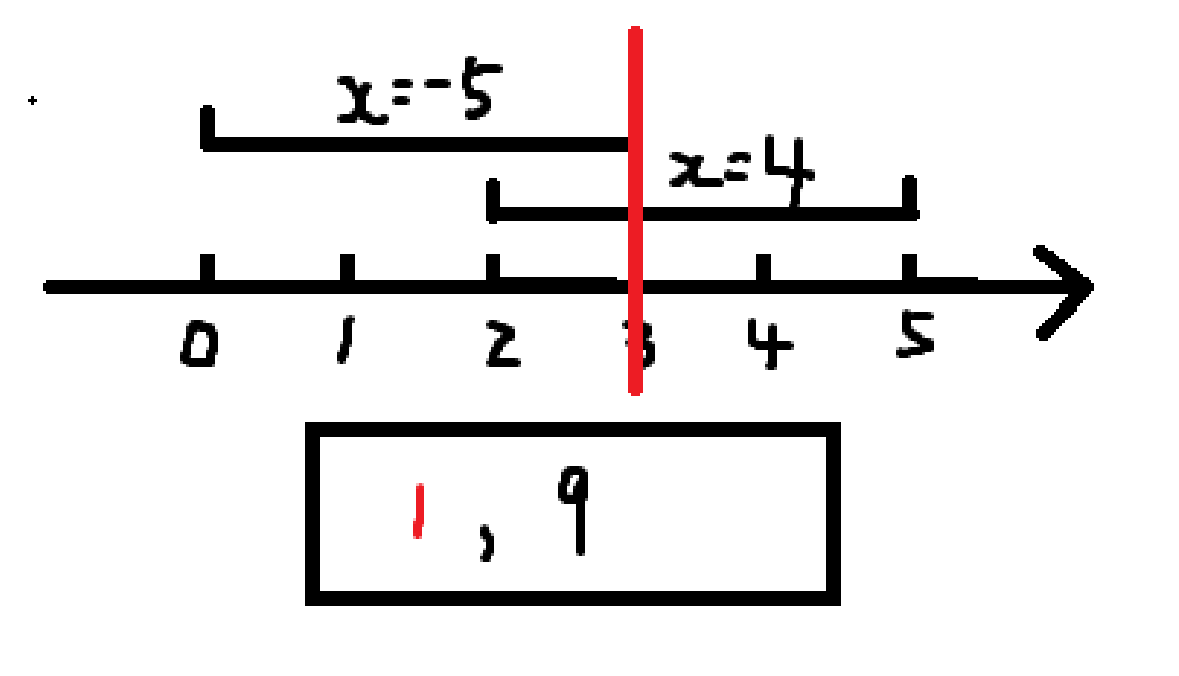
然后扫描线扫到 \(4\),全局加 \(4\),于是变成这个样子:
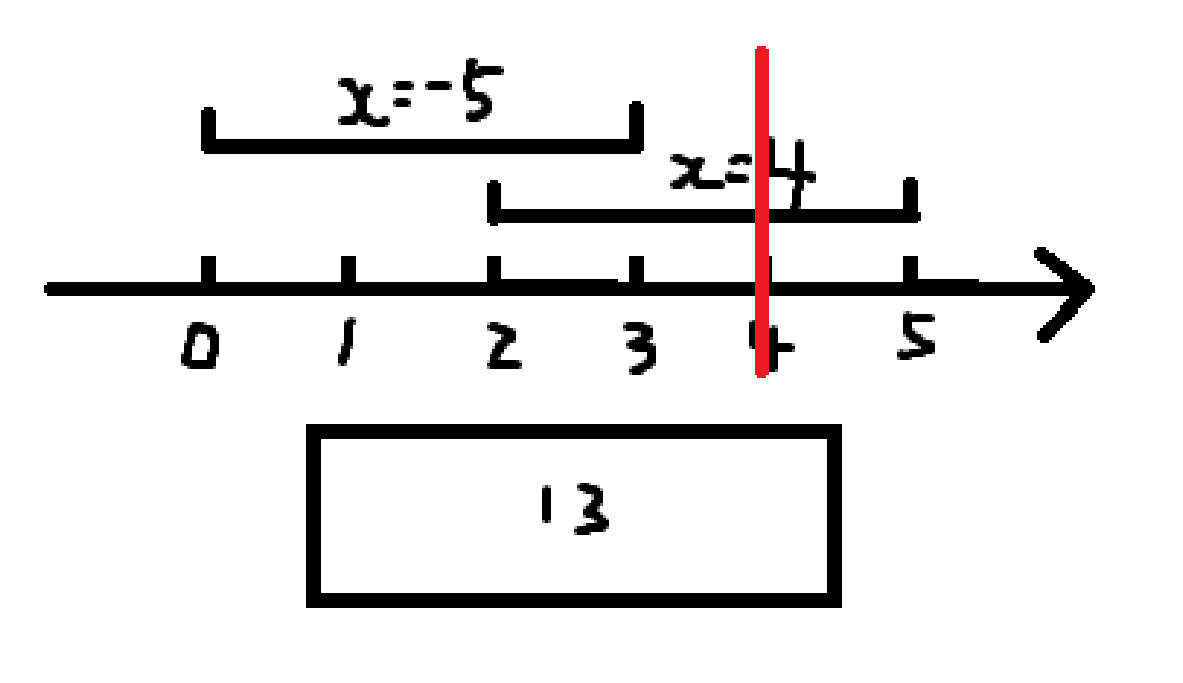
然后扫描线扫到 \(5\),全局加 \(5\),我们发现这个位置是第 \(2\) 个询问的右端点,所以第 \(2\) 个询问的答案就是 \(18\),于是变成这个样子:
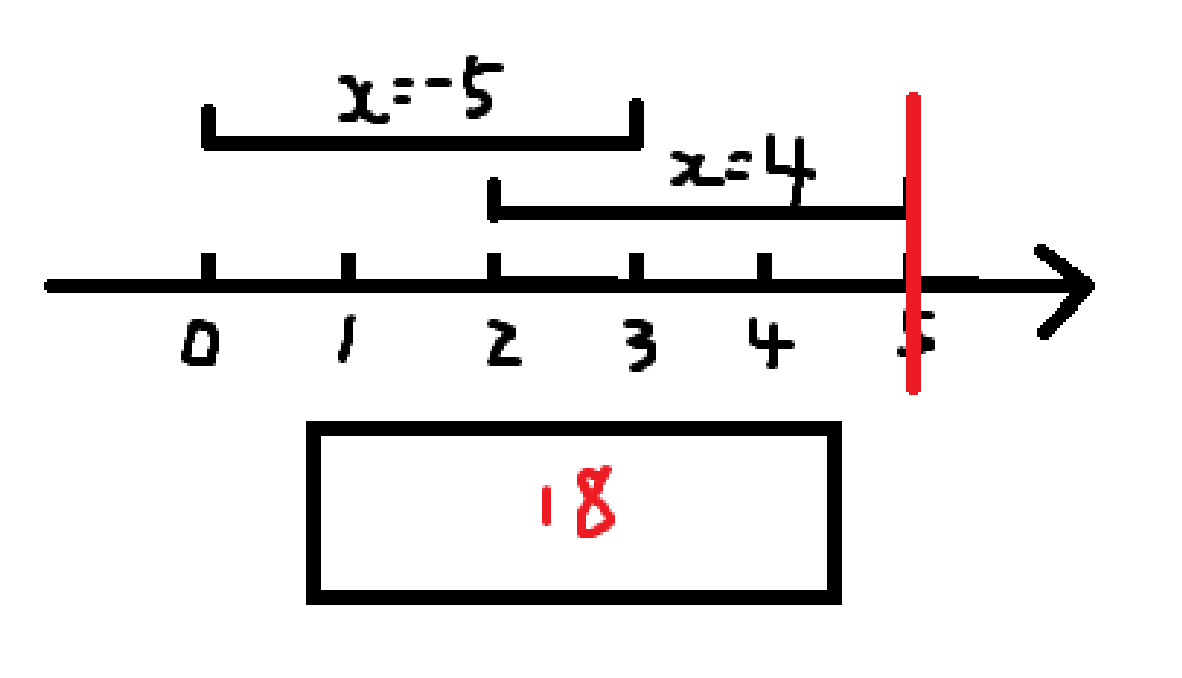
至此,答案全部求出,算法结束。
实现细节
在看图解的时候,想必大家发现了好多细节问题,接下来一一阐明:
- Q:怎么知道数据结构中每个询问对应的节点呢?
A:开一个指针数组 \(it\),\(it_i\) 指向数据结构中的第 \(i\) 个询问对应的节点。 - Q:数据结构全局修改都有懒标记,查询时如何确保标记已经全部下传呢?
A:对于每个节点,开一个 \(fa\) 指针,查询前写一个递归即可。
例题与代码
题目大意
给定一个常数 \(p\) 和长度为 \(n\,(1\le n\le 10^6)\) 的数组 \(a\),定义 \(f_i(x)=x+a_i-[x+a_i\ge p]\times p\,(i\in[1,n])\)。
给定 \(m\) 个询问,每个询问给定 \(l,r\),求 \(f_r(f_{r-1}(\dots f_{l+2}(f_{l+1}(f_l(0)))\dots))\)。
这题就是这个算法的模板加一个有交合并(详见代码)平衡树,思路不多赘述。
Code
这道题虽是模板,但被卡常,如果你 \(\text{Time limit exceeded on test}\ge\text{10}\),那么你就对了。
#include <bits/stdc++.h>
using namespace std;
#define int long long
constexpr int maxn = 1000010;
struct question {
int l, r, i;
} ql[maxn], qr[maxn]; // ql: 对 l 排序,qr:对 r 排序
int n, m, p, a[maxn], ans[maxn], it[maxn]; // it 为指针,ans 为答案
struct FHQnode {
int v, ran, ls, rs, tag, fa;
} ;
struct FHQtreap {
FHQnode node[maxn];
int cnt, root;
void pushup(int u) { // 前文的细节 2,维护 fa
node[u].fa = 0;
if (node[u].ls) node[node[u].ls].fa = u;
if (node[u].rs) node[node[u].rs].fa = u;
return ;
}
void pushdown(int u) {
node[node[u].ls].v += node[u].tag;
node[node[u].ls].tag += node[u].tag;
node[node[u].rs].v += node[u].tag;
node[node[u].rs].tag += node[u].tag;
node[u].tag = 0;
return ;
}
void split(int u, int &l, int &r, int x) {
if (!u) {
l = r = 0;
return ;
}
pushdown(u);
if (node[u].v <= x) {
l = u;
split(node[u].rs, node[u].rs, r, x);
node[u].fa = 0;
} else {
r = u;
split(node[u].ls, l, node[u].ls, x);
}
pushup(u);
return ;
}
int merge(int l, int r) {
if (!l || !r) return l + r;
if (node[l].ran <= node[r].ran) {
pushdown(l);
node[l].rs = merge(node[l].rs, r);
pushup(l);
return l;
} else {
pushdown(r);
node[r].ls = merge(l, node[r].ls);
pushup(r);
return r;
}
}
int Merge(int l, int r) { // 与这个算法关系很深的技巧(用的非常多): 平衡树有交和并,详见 https://rainlycoris.github.io/posts/P5494/(by @DaydreamWarrior in luogu)
if (!l || !r) return l + r;
int L, R;
if (node[l].ran <= node[r].ran) {
split(r, L, R, node[l].v);
pushdown(l);
node[l].ls = Merge(node[l].ls, L);
node[l].rs = Merge(node[l].rs, R);
pushup(l);
return l;
} else {
split(l, L, R, node[r].v);
pushdown(r);
node[r].ls = Merge(node[r].ls, L);
node[r].rs = Merge(node[r].rs, R);
pushup(r);
return r;
}
}
void ins(int i) {
node[++cnt] = {0, rand(), 0, 0, 0, 0};
it[i] = cnt;
int l, r;
split(root, l, r, 0);
root = merge(merge(l, cnt), r);
return ;
}
void update(int k) {
node[root].tag += k;
node[root].v += k;
int l, r;
split(root, l, r, p - 1);
node[r].tag -= p;
node[r].v -= p;
root = Merge(l, r);
return ;
}
void pushalldown(int u) { // 前文的细节 1
if (node[u].fa) pushalldown(node[u].fa);
pushdown(u);
return ;
}
} t;
signed main() {
srand((unsigned)time(NULL));
ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr);
cin >> n >> m >> p;
for (int i = 1; i <= n; i++) {
cin >> a[i];
}
for (int i = 1; i <= m; i++) {
ql[i].i = i;
cin >> ql[i].l >> ql[i].r;
}
for (int i = 1; i <= m; i++) {
qr[i] = ql[i];
}
sort(ql + 1, ql + 1 + m, [](question a, question b){return a.l < b.l;});
sort(qr + 1, qr + 1 + m, [](question a, question b){return a.r < b.r;}); // 排序,为后面的双指针做准备
for (int i = 1, j = 1, k = 1; i <= n; i++) {
while (ql[j].l == i) { // 双指针
t.ins(ql[j].i);
j++;
}
t.update(a[i]);
while (qr[k].r == i) { // 双指针
t.pushalldown(it[qr[k].i]);
ans[qr[k].i] = t.node[it[qr[k].i]].v;
k++;
}
}
for (int i = 1; i <= m; i++) {
cout << ans[i] << '\n';
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号