L01_机器学习基本概念(李宏毅机器学习_学习笔记)

目录

• 什么是机器学习
  • 不同类别的函数(Function)
    • 1. 回归(Regression)
    • 2. 分类
    • 3. 结构化学习
• 如何找到想要的函数(Function)
  • 1.建立一个含有位置参数的函数
  • 2.定义损失函数
  • 3.最优化(Optimization)
• 模型的变形：\(Sigmoid\to ReLU\)
• 总结

什么是机器学习

让机器具有寻找一个函数(Function)的功能

不同类别的函数(Function)

1. 回归(Regression)

函数输出一个标量

2. 分类

给出不同的选项，函数输出正确的那一个。

3. 结构化学习

产生一个有结构的物件，比如画一张图，写一篇文章。

如何找到想要的函数(Function)

1.建立一个含有位置参数的函数

我们可以使用线性的函数进行训练，但是使用线性模型太过简单，无法很好的模拟出现实的情况，我们需要更加复杂的模型我们可以使用constant + sum of a set of Sigmoid Function逼近不同的曲线

Sigmoid Function(S型曲线)：

\[\begin{align*} y &= c\dfrac{1}{1+e^{-(b+wx_{1})}}\\ &= c\cdot sigmoid(b+wx_{1}) \end{align*} \]

不同参数的影响如下图所示:

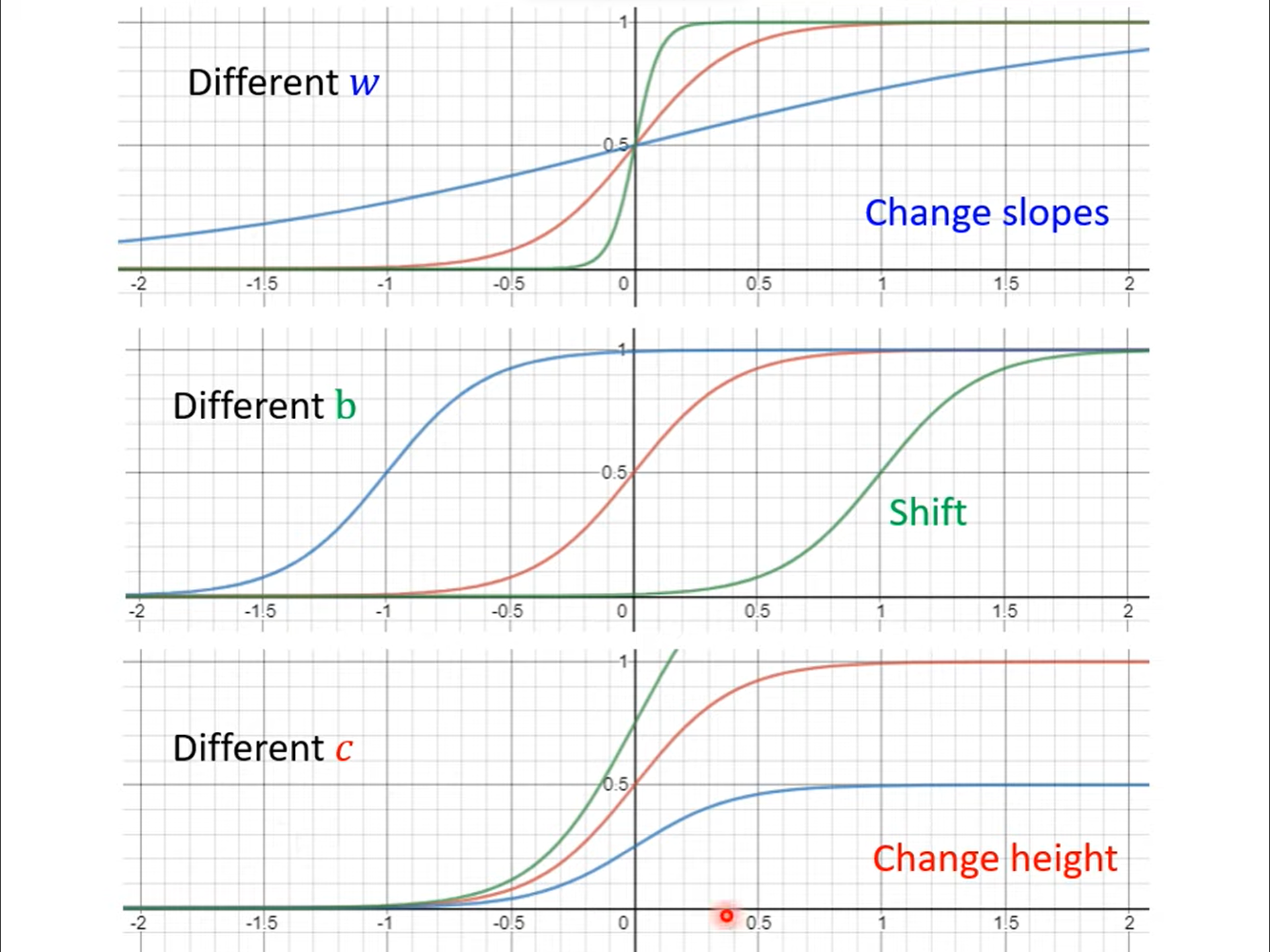
所以我们可以进一步写出新的Model：

\[y=b+\sum_{i}c_{i}\cdot sigmoid(b_{i}+w_{i}x_{1}) \]

如果我们利用多个已知的数据(features)进行预测，则有：

\[y=b+\sum_{i}c_{i}\cdot sigmoid(b_{i}+\sum_{j} w_{ij}x_{j}) \]

其中，\(j\) 是 \(features\) 的编号，\(i\) 是 \(sigmoid\) 的编号。

使用线性代数的知识对式子进行化简可以得到：

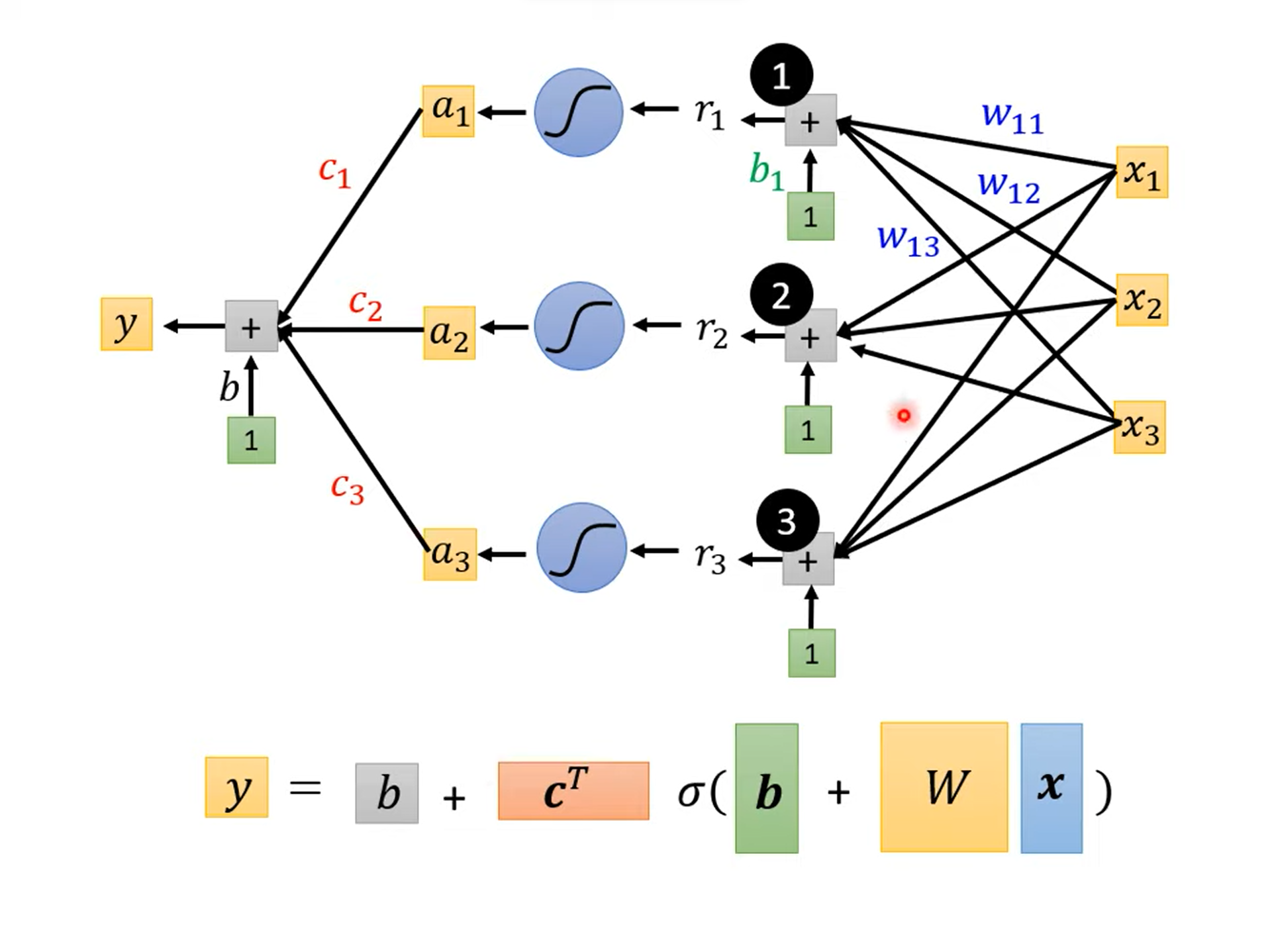
可以将所有的未知参数构成一个向量\(\theta\)：

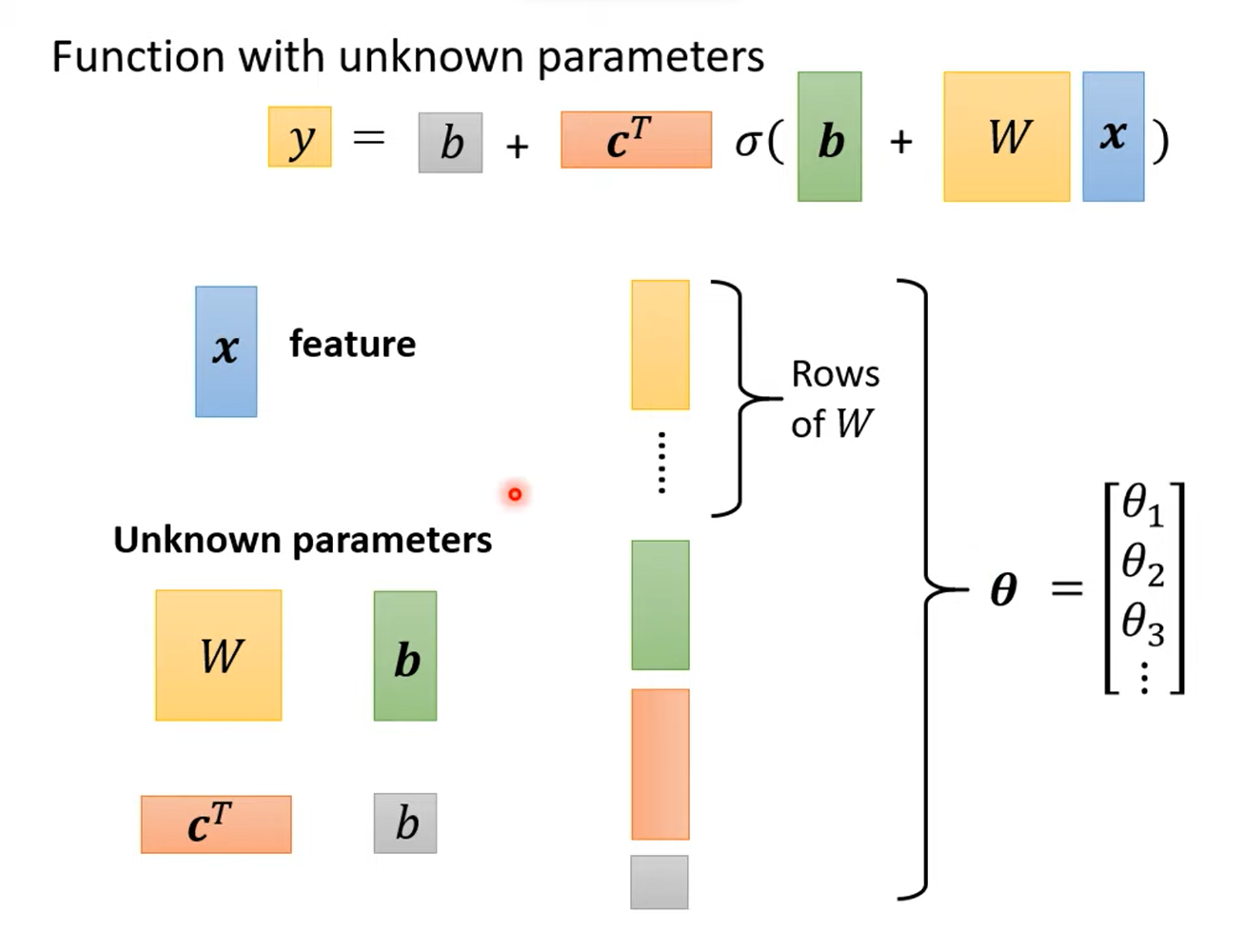
2.定义损失函数

损失函数是所有参数的函数\(L(\mathbf{\theta})\)，表示使用一组参数建立起的模型的好坏。

\[e=\hat{y}-y \\ Loss:\quad \frac{1}{N}\sum_{n}e_{n} \]

3.最优化(Optimization)

找一组最优的参数\(\theta^{*}=arg\quad \mathop{min}\limits_{\theta}L\)

使用梯度下降(Gradient Descent)

• 随机选取一个初始值\(\mathbf{\theta^{0}}\)

• 计算梯度\(\mathbf{g}=\nabla L(\mathbf{\theta^{0}})\)

  接着计算

  \(\mathbf{\theta^{1}}\gets \mathbf{\theta^{0}} - \eta\mathbf{g}\)

  \(\mathbf{\theta^{2}}\gets \mathbf{\theta^{1}} - \eta\mathbf{g}\)

  \(\cdots\cdots\)

• 迭代更新\(\mathbf{\theta}\)的值

但是在实际的最优化过程中，我们将很多的数据分成好多份，每一份算出一个\(L^{i}\)出来，然后使用它迭代计算\(\mathbf{\theta}^{*}\)。具体过程如下图所示：

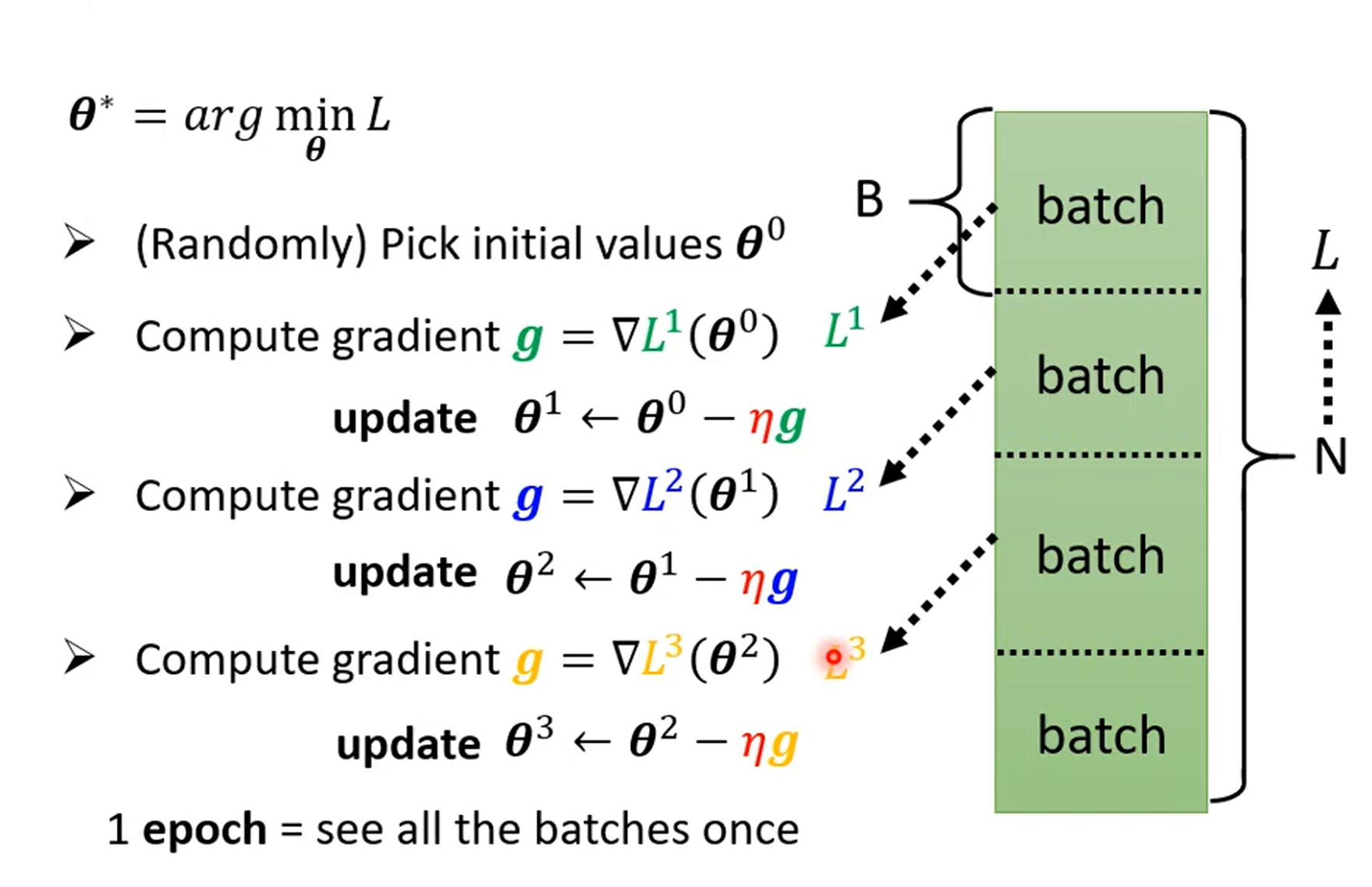
\(\textbf{update}\)：是使用一个\(batch\)中的数据训练出的\(L\)迭代一次。

\(\textbf{epoch}\)：使用每一个\(batch\)迭代过一次\(\mathbf{\theta}\)。

模型的变形：\(Sigmoid\to ReLU\)

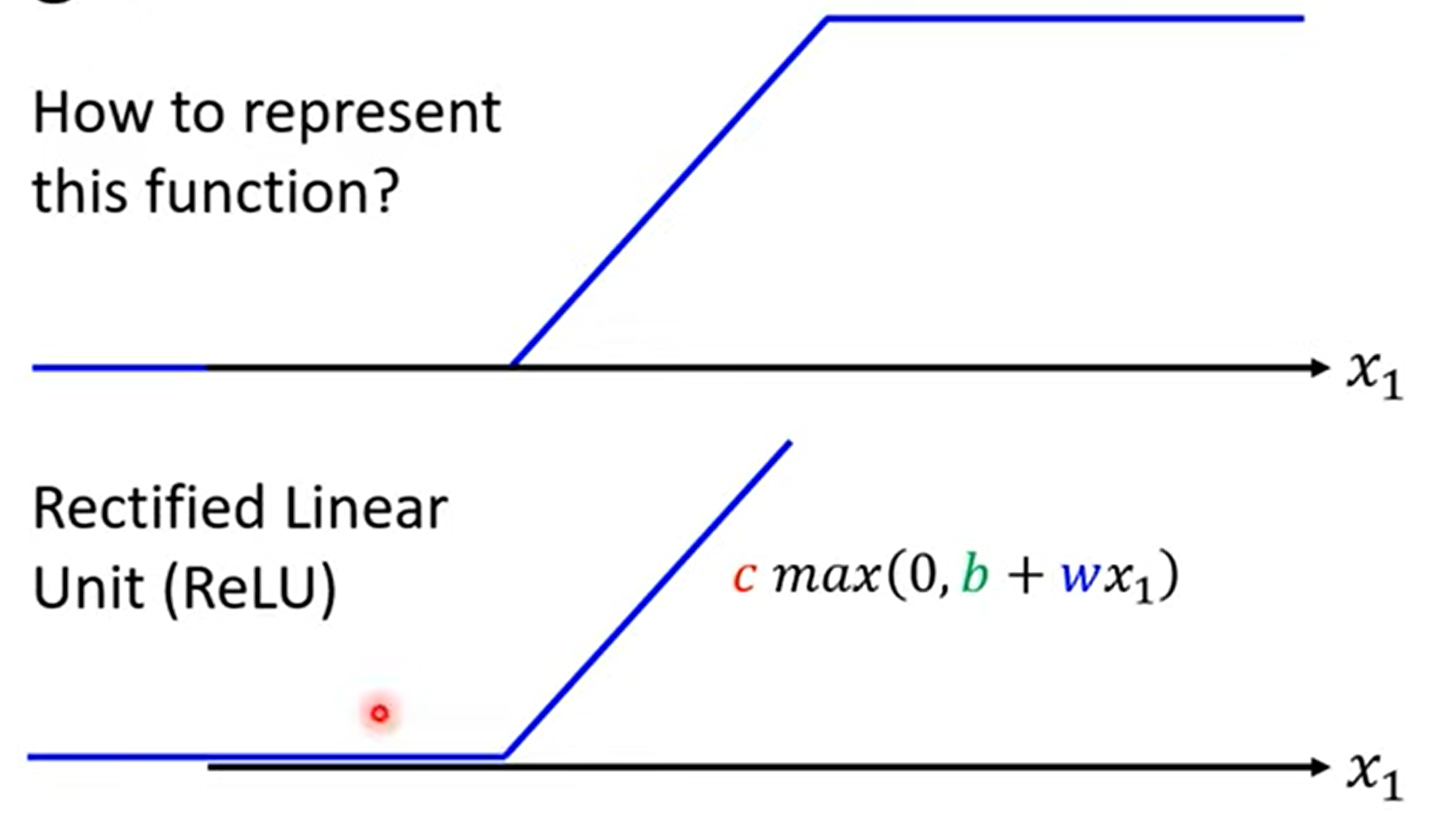
两个\(ReLU\)可以形成一个\(HardSigmoid\)

总结

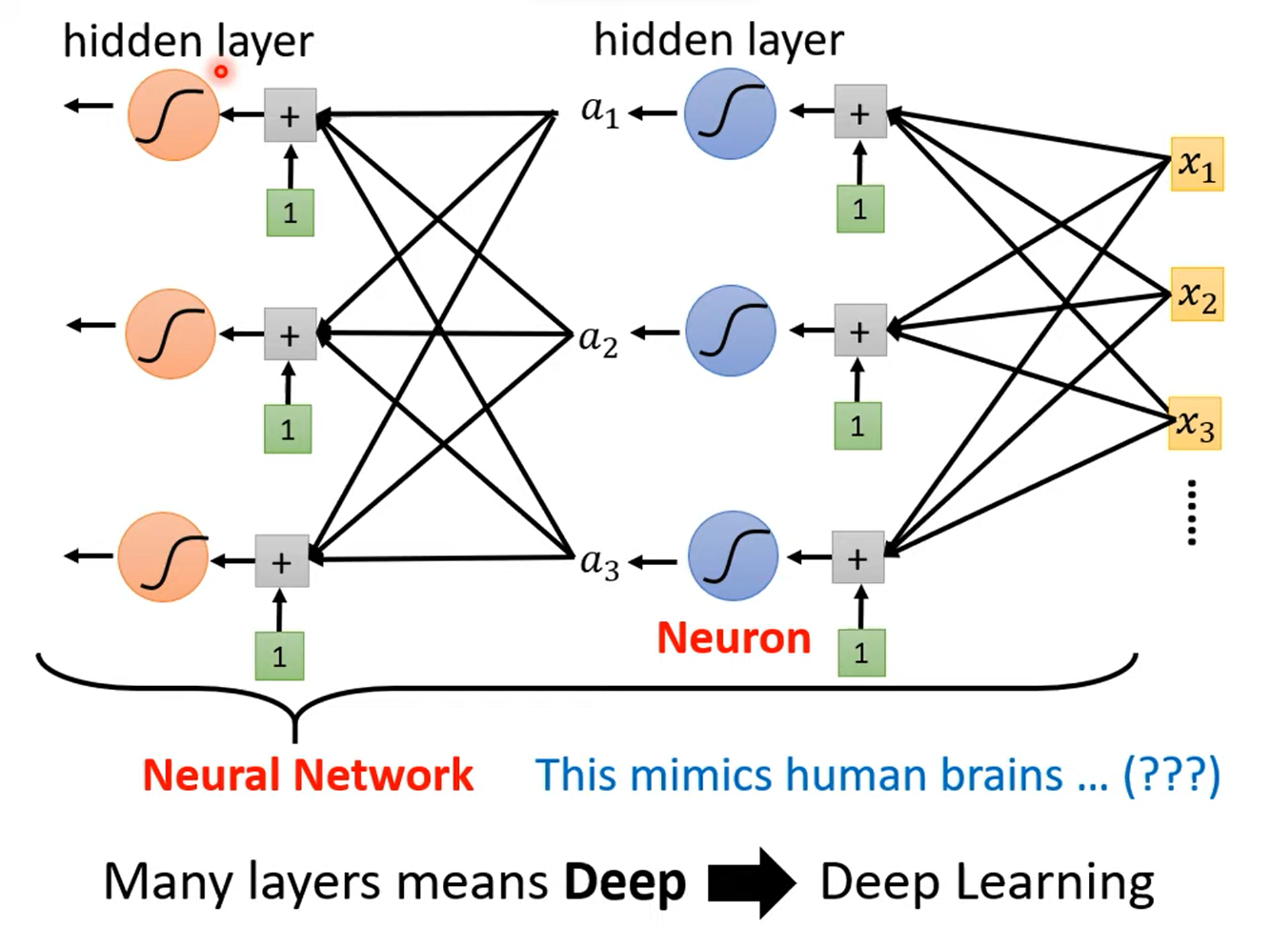
但是，随着\(layer\) 逐渐的加深，可能会出现在训练数据上较好，在预测数据上却比较差的情况，我们称它作\(\textbf{overfitting}\)。

文章中所有图片均来源与李宏毅老师的2021年机器学习课程