切割线放缩

这两天一直在刷导数大题，一个题经常是做近半个小时做不出来看答案，一个题下来几乎要用上一个小时的时间，而在这个过程中发现了很牛逼的东西，切割线放缩。

首先先说一下这东西大概啥时候用，一般碰到只有一个极值点，并且函数又增减性变化的函数，和有一条水平线的情况使用。

形式化来说就是一个函数 \(f(x)=a\) 的解分别为 \(x_1,x_2\)，要求证明 \(x_1 \pm x_2 < b+(a)\)，其中 \(b\) 是常数，不等号的方向不固定。

接下来来道例题讲解一下这个东西。

例如这道2021全国新高考Ⅰ卷的压轴22题

第一问不说。

第二问对于 \(2<\frac{1}{a}+\frac{1}{b}\) 的情况，直接将 \(\frac{1}{a}，\frac{1}{b}\) 换元，然后就是最典的那道极值点偏移了。

具体讲解后面的情况，后面这东西我看答案给了一个很傻逼的放缩，感觉我不是很能独立想出来，刚好庭哥说这个题可以切割线放缩我们来尝试一下。

首先我们先画出 \(f(x)\) 的图像，大概就长这样

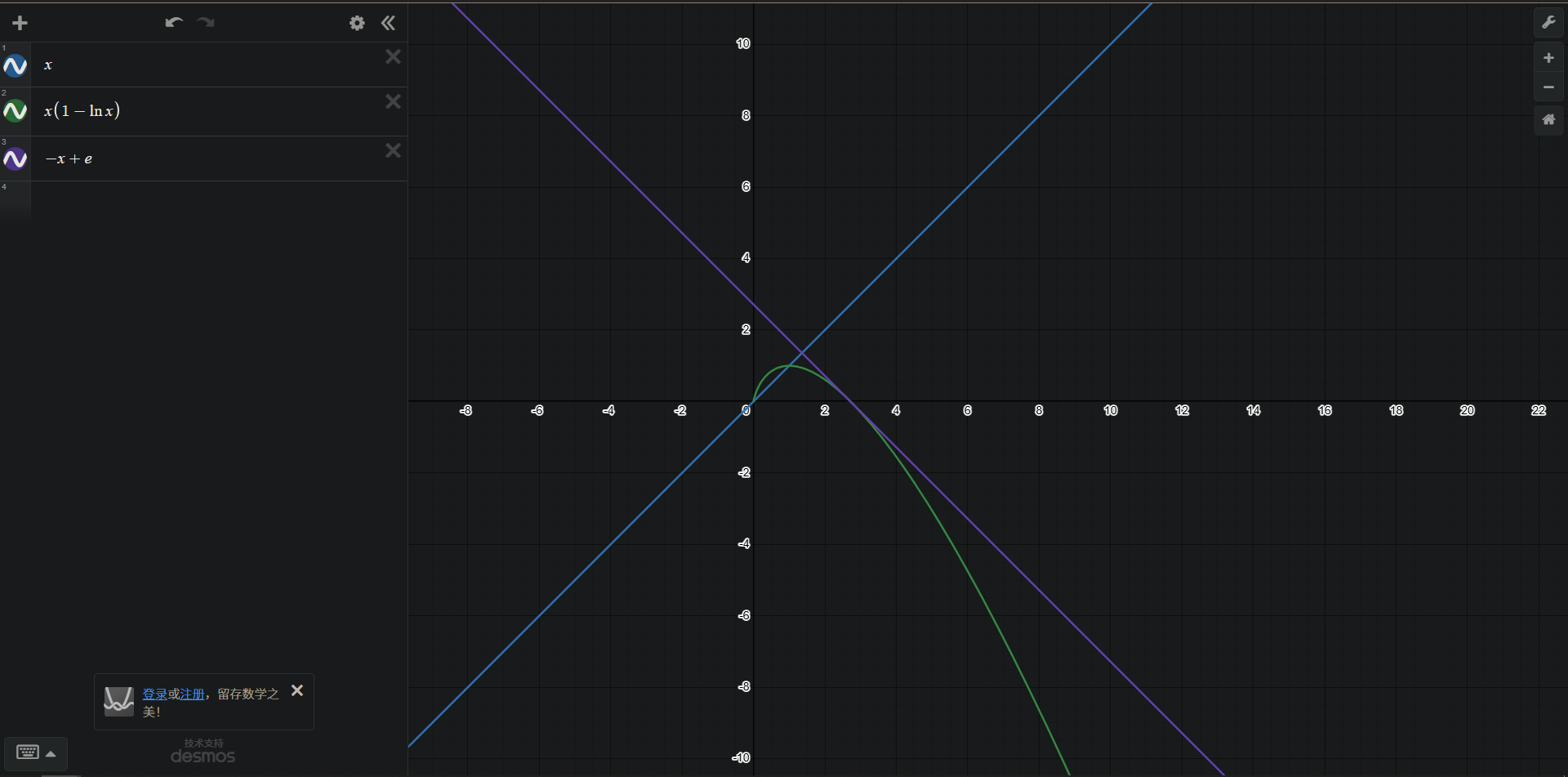
绿色的是图像，剩下两条直线是后面用的切割线。

我们一般使用过函数零点的切线来放缩（这算是一种约定俗成吧好像），显然 \(f(x)\) 的一个零点是 \(e\)，我们可以得到这条切线方程 \(y=-x+e\)，我们随便设一条水平线 \(y=a\)，那么我们设 \(x_1,x_2\) 分别是 \(f(x)=a\) 的两个解，令 \(x_1 < x_2\)。我们已知切线方程，那么当 \(y=a\) 时，切线的横坐标就是 \(e-a\)，并且根据图像可以看出一定有 \(e-a>x_2\)，也可以直接求导证，这里方便我就直接用眼盯了。而题目要求我们证明 \(x_1+x_2<e\)，那么我们现在只需要证明 \(x_1 < a\) 即可，我们尝试将 \((a,a)\) 和极值点放到一条直线上，组成一条函数的割线，于是就有了 \(y=x\) 这条直线，我们用眼盯刚好发现这条线在 \([0,1]\) 时刚好在函数内部（我也不知道叫啥了，我觉得这么叫比较形象），于是可以得到 \(x_1<a\)，原命题得证。

后话：还有一道比较好的题，但是那个计算量我感觉比这个大很多，所以只选了这个。貌似这个东西当时并不流行，这两年才兴起的，傻逼出题人。