「Solution」 BZOJ3894 文理分科

Problem

Link

题意：有 \(n*m\) 个同学，每个同学选科目有一个满意值，若 ta 上下左右的同学与 ta 选的科目相同则有额外的满意值，求最大的满意值。

Solution

利用最小割的思路来做，问题转化为 总贡献-最小割。

考虑建模。

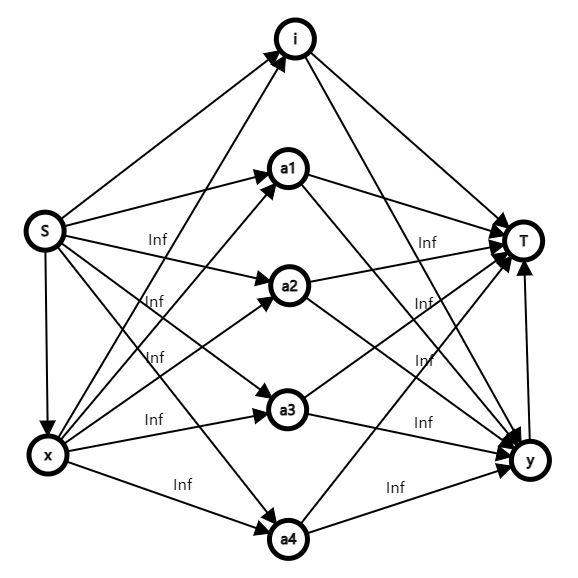
\(s \rightarrow i\) 容量为 \(i\) 选文科的贡献。

\(i \rightarrow t\) 容量为 \(i\) 选理科的贡献。

\(a1,a2,a3,a4\) 同理。

\(s \rightarrow x\) 容量为同选文科的贡献。

\(y \rightarrow t\) 容量为同选理科的贡献。

我们来证明一下，每一个割法下来都是一个合法（符合题目定义）的方案。

一条容量为正无穷的边，则意味这这条边不会被割。

• 当 \(i,a1,a2,a3,a4\) 选理。

则 \(s \rightarrow i\) 被割掉，\(a1,a2,a3,a4\) 同样被割。

最后发现还可以通过 \(s \rightarrow x\) 走向 \(T\) ，则 \(s \rightarrow x\) 也要被割掉。所以割贡献就是 \(i,a1,a2,a3,a4\) 的选文的贡献 + 同文的贡献。最终得到的就是都选理的贡献。（都选文科同理）

• 当 \(i\) 选理，\(a1\) 选文，\(a2-a4\) 随便选。即选科不相同。

这说明已经不能得到同选理科的贡献了。

割掉每个点没选的科目的边后，则直接通过 \(S \rightarrow node \rightarrow T\) 的路径已经没有了。只有通过 \(x,y\) 两点的路了。

不难发现存在 \(S \rightarrow a1 \rightarrow y \rightarrow T\) 的路径，由于 \(S \rightarrow a1\) 不能割，\(a1 \rightarrow x\) 容量为无穷也不能割，所以只能割掉 \(y \rightarrow T\)。\(S \rightarrow x \rightarrow i \rightarrow T\) 同理。

所以既不是全选文科，也不是全选理科的情况一定不会算上同选文和同选理的贡献。

Code

//by Poison
//c++11 Dinic
#include <queue>
#include <cstdio>
#include <vector>
#include <algorithm>

using namespace std;

#define Maxn 500
#define LL long long
#define rep(i, j, k) for(int i = (j); i <= (k); i ++)
#define per(i, j, k) for(int i = (j); i >= (j); i --)

int dx[4] = {0, 1, 0, -1};
int dy[4] = {1, 0, -1, 0};

struct Score {
	int art, science;
	int sart, sscience;
} a[Maxn + 5][Maxn + 5];

struct Flow_Edge {
    int v, u;
    long long cap, flow = 0;
    Flow_Edge (int v, int u, LL cap) : v (v), u (u), cap (cap) {}
} ;

struct Dinic {
    const LL Maxn_Flow = 1e18;

    int n, m = 0, s, t;
    queue < int > q;
    vector < int > ptr, level;
    vector < Flow_Edge > edge;
    vector < vector < int > > adj;

    Dinic (int n, int s, int t) : n (n), s (s), t (t) {
        adj.resize (n + 1);
        ptr.resize (n + 1);
        level.resize (n + 1);
    }

    void Add_Edge (int v, int u, LL c) {
        edge.emplace_back (v, u, c);
        edge.emplace_back (u, v, 0);
        adj[v].push_back (m);
        adj[u].push_back (m + 1);
        m += 2;
    }

    bool Bfs () {
        while (q.size ()) {
            int v = q.front (); q.pop ();
            for (int id : adj[v]) {
                if (edge[id].cap - edge[id].flow < 1) continue;
                if (level[edge[id].u] != -1) continue;
                level[edge[id].u] = level[v] + 1;
                q.push (edge[id].u);
            }
        }
        return level[t] != -1;
    }

    LL Dfs (int v, LL pushed) {
        if (!pushed) return 0;
        if (v == t) return pushed;
        for (int& i = ptr[v]; i < (int) adj[v].size (); i ++) {
            int id = adj[v][i];
            int u = edge[id].u;
            if (level[v] + 1 != level[u] || edge[id].cap - edge[id].flow < 1) continue;
            LL tr = Dfs (u, min (pushed, edge[id].cap - edge[id].flow));
            if (!tr) continue;
            edge[id].flow += tr;
            edge[id ^ 1].flow -= tr;
            return tr;
        }
        return 0;
    }

    LL Flow () {
        LL f = 0;
        while (true) {
            fill (level.begin (), level.end (), -1);
            level[s] = 0;
            q.push (s);
            if (!Bfs ()) break;
            fill (ptr.begin (), ptr.end (), 0);
            while (LL pushed = Dfs (s, Maxn_Flow)) f += pushed;
        }
        return f;
    }
} ;

int main () {
    int n, m;
    scanf ("%d %d", &n, &m);
    
    int tot = 0;
    rep (i, 1, n) 
    	rep (j, 1, m) {
    		scanf ("%d", &a[i][j].art);
			tot += a[i][j].art;
		}
	rep (i, 1, n) 
    	rep (j, 1, m) {
    		scanf ("%d", &a[i][j].science);
			tot += a[i][j].science;
		}
	rep (i, 1, n) 
    	rep (j, 1, m) {
    		scanf ("%d", &a[i][j].sart);
			tot += a[i][j].sart;
		}
	rep (i, 1, n) 
    	rep (j, 1, m) {
    		scanf ("%d", &a[i][j].sscience);
			tot += a[i][j].sscience;
		}
    	
	Dinic T (n * m * 3 + 1, 0, n * m * 3 + 1);
	int s = 0, t = n * m * 3 + 1;
	
	rep (i, 1, n) {
		rep (j, 1, m) {
			T.Add_Edge (s, (i - 1) * m + j, a[i][j].art);
			T.Add_Edge ((i - 1) * m + j, t, a[i][j].science);
			T.Add_Edge (s, n * m + (i - 1) * m + j, a[i][j].sart);
			T.Add_Edge (n * m * 2 + (i - 1) * m + j, t, a[i][j].sscience);
			T.Add_Edge (n * m + (i - 1) * m + j, (i - 1) * m + j, 1e18);
			T.Add_Edge ((i - 1) * m + j, n * m * 2 + (i - 1) * m + j, 1e18);
			rep (k, 0, 3) {
				int x = i + dx[k];
				int y = j + dy[k];
				if (x < 1 || y < 1 || x > n || y > m) continue;
				T.Add_Edge (n * m + (i - 1) * m + j, (x - 1) * m + y, 1e18);
				T.Add_Edge ((x - 1) * m + y, n * m * 2 + (i - 1) * m + j, 1e18);
			} 
		}
	}
	
	printf ("%lld", tot - T.Flow ());
    return 0;
}