复健计划
10.18
T1 向量
给 \(n\) 位数字(\(n\le2e5\)),每次操作将两位数字合并,如果合并后仍为两位数,则写成两位数的形式,求最大操作次数。
结论:操作次数总是固定的。考虑数字总和,合并要么不变要么 \(-10\),所以感性理解和跟顺序没有关系,大于 \(10\) 就减。
T2 顺序

构造,显然下界为 \(n+m-2\),上界为 \(nm-1\)。
考虑对下界的构造,构造成一个王字。
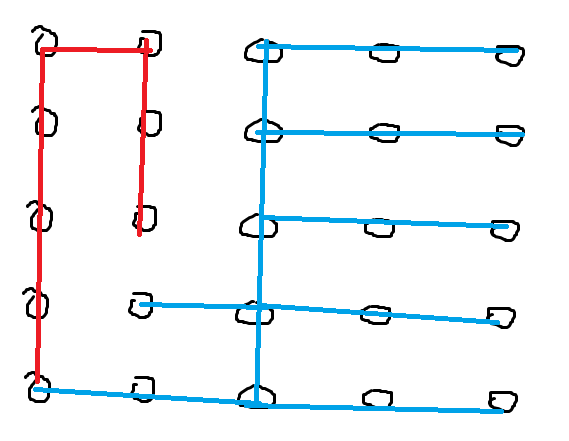
蓝线是下界骨架,红线走 \(s\) 构造下界与上界之间的值。
注意如果 \(n,m\) 都是偶数取不到下界且与奇数有一定区别,一奇一偶可以交换 \(nm\),最后输出调换即可。
T3 缺损的表达式
建表达式树直接 \(dp\) 即可。
T4 熵值

每次操作都减少一个 \(d\),所以两个点最多操作一次,且不会成环,换言之,这些点最后将会形成森林。对于每个联通块,最小代价是最小生成树,最后 \(dp\) 即可。
10.18
T2

结论:在所有 \(2t+1\) 个字符串中,存在一个唯一出现次数为奇数的字母,出现的字母要么后面不变在最后一个字符串出现,要么被替换时出现。
T4
给定长度为 \(n\) 的序列,求 \(mex\) 为 \(0\) 到 \(n\) 的子序列个数。
给一组样例分析:
固定左端点为 \(1\),则 \(mex\) 为:
左端点右移一位,则 \(mex\) 为:
分析可以发现,在左端点由 \(i\) 变为 \(i+1\) 的过程中,\(mex\) 数组发生改变的是一段区间,左边界是第一个大于 \(a_i\) 的,右边界为下一个 \(a_i\) 的位置减一。用 \(set\) 维护连续段和时间戳即可。
11.5
B
给一个完全图 \(G\),\(|G|\le3000\) ,每次询问加入一条边,求最小生成树的权值和。
用一种新式的求最小生成树方法,令 \(S\) 为未加入的点集,\(T\) 为最小生成树中的点集,类似 \(dij\) 每次把距离 \(S\) 集合最小的点加入进 \(T\) 并修改信息,可以做到 \(O(n^2)\)。
然后每次修改就删一条加一条 \(O(qn)\)。
D
有一个 \(k\times k\) 的矩阵(\(k\) 并未给出),其中每个格子的石子数 \(\ge m\),且对角线格子石子数和小于等于 \(n\),任意选择 \(k\) 个行和列都不相同的格子石子数都一样。
最后一个限制很强可以从最后一个格子开始推。由题意 \(a_{x,i}+a_{y,j}=a_{x,j}+a_{y,i}\),于是得到 \(a_{x,i}-a_{y,i}=a_{x,j}-a_{y,j}\),这启发我们转化问题,对 \(k\) 行 \(k\) 列都赋一个权值,\(a_{i,j}=x_i+y_j\),这个矩阵合法,显然这是充分的。考虑和小于 \(n\),先减去 \(k\times m\),剩下的值分配到 \(2k\) 个行列权值中(可以有剩余),可能算重(\(x\) 加 \(y\) 减),限制至少一个为 \(0\),方案数为 \(\dbinom{n-k\times m+2k}{2k}-\dbinom{n-k\times m+k}{2k}\)
11.26
B
在一条数轴上,有 \(n\) 个杆子,价格为 \(c_i\),若当前位置为 \(x\),则可以跳到 \(x-v_i\) 和 \(x+v_i\) 上(购买后可以重复用),求走到任意一个格子上的最小费用。
转化能走到每一个格子的条件为选出若干个杆子 \(\gcd_{v_i}=1\)。发现钦定某个杆子必选以后最多只有 \(\log\) 个质因数,爆搜即可。
C
不是很会描述。

考场上脑子太死了。考虑先把原序列分为一个个块,设块的个数为 \(m\),那么有 \(m!\) 种排列符合条件,但是这样做是忽略了两个块拼成一个块的情况,考虑容斥,设合并后块的个数为 \(x\) 那么贡献是 \(x!\times 2^{d}\times(-1)^{m-x}\),这里的 \(d\) 是不为 \(1\) 的个数,次幂是因为长度不为一的块可以左右调换。
直接做是 \(O(n^3)\) 的,考场倒在这里是没想到的。把容斥系数装进 \(dp\)。令 \(f_{i,j}\) 为处理完前 \(i\) 个块,合并完剩下 \(j\) 个块的答案。
如果 \(a_i=1\) 有 \(f_{i,j}=f_{i-1,j-1}\times(-1)\times j\),否则 \(f_{i,j}=f_{i-1,j-1}\times(-2)\times j\)
如果不从 \(i-1\) 转移过来那么填入的数肯定不是 \(1\) 了。
\(f_{i,j}=\sum_{k=0}^{i-2}f_{k,j-1}\times(-2)\times j\)
容易优化。
D
好像是 border 论啥的,不会。
11.28
简单写一下。
A
求有多少个可重集的和等于 \(n\),其中 \(n\le10^5\)。
根分,如果可重集只有 \(\le \sqrt n\) 的数,可以用完全背包,发现这个时候集合大小是大于的 \(\sqrt n\)。
集合小于等于 \(\sqrt n\) 可以 \(dp\),令 \(f_{i,j}\) 为 \(i\) 个元素,和为 \(j\)。两种转移,一种是直接加入一个 \(1\),另外一种是全部加一。
B
不难的题。给 \(l_i,r_i,w_i\) 表示将编号在 \(l_i\) 到 \(r_i\) 之间的点两两之间连一条权值 \(w_i\) 的边,求 \(1\) 到 \(n\) 的最短路长度。
考虑一个点 \(u\) 从 \(v\) 转移过来,如果转移过来的这条边对应的 \(l_i \le v\) 那么可以也从 \(l_i\) 转移,所以按 \(l_i\) 扫描线,每次到 \(r_i\) 与 \(w_i+dis_i\) 取 \(\min\),其中 \(dis_i\) 表示走到 \(i\) 的最短路径长度。
D
给一棵树,两个聪明人玩游戏,轮流移动旗子,限制要比上一个人移动的距离远,走不了时游戏结束,求旗子在树上的每一个点是先手必胜还是后手必胜。
考虑一个链编号为 \(1\dots n\),显然旗子在 \(1\) 和 \(n\) 先手必胜,往内缩,考虑 \(2\) 和 \(n-1\),发现我们可以走对应的点使得对手下一步走到 \(1\) 或 \(n\)。
一直往内缩,如果长度为奇数则中间那个点是后手必胜,先手不管走到哪都是先手必胜点,其余情况都是先手必胜。
考虑树,把树的直径拉出来,发现树的直径以外的点实际上可以在直径找到和他等价的点,做法同链。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号