图论中的一些名词的定义。

最近zkx大佬在学图论，有一些定义很秀，压根读不懂，所以按照自己的理解来总结一下。

ps:在不同的情况下可能定义不同，要根据上下文感性理解

比较基础的

图

图：将点用边连起来，点与边共同组成图。
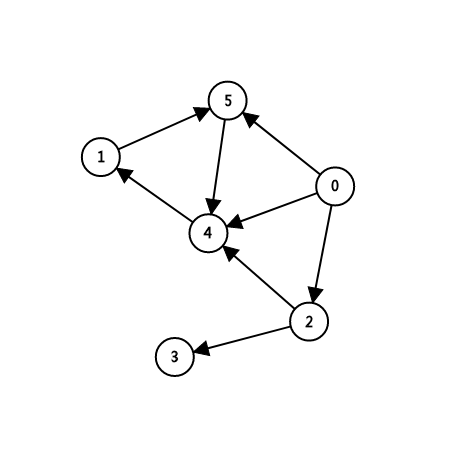
下面这两个都是图。

有向图

有向图：连接点的边有方向（只能按照边的方向走）。

上面的左图就是有向图,可以从 \(0\) 走到 \(2\)，但不能从 \(2\) 走到 \(0\)。

无向图

无向图：连接点的边没有方向（相当于两条反向的有向边）。

上面的右图就是无向图,可以从 \(0\) 走到 \(2\)，也可以从 \(2\) 走到 \(0\)。

节点的入度

入度：在有向图（上图左）中，以这个点为终点的边的数目叫做这个点的入度。

上图左中以 \(4\) 号点为终点的边有 \(0 \rightarrow 4\)、\(1 \rightarrow 4\)、\(2 \rightarrow 4\) 所以 \(4\) 号点的入度为 \(3\)。

节点的出度

出度：在有向图（上图左）中，以这个点为起点的边的数目叫做这个点的出度。

上图左中以 \(0\) 号点为起点的边有 \(0 \rightarrow 2\)、\(0 \rightarrow 3\)、\(0 \rightarrow 4\) 所以 \(0\) 号点的出度为 \(3\)。

节点的度

度：在无向图（上图右）中，连接这个点的边的数目叫做这个点的度。

上图右中连接 \(4\) 号点的边有 \(0 \leftrightarrow 4\)、\(1 \leftrightarrow 4\)、\(2 \leftrightarrow 4\)、\(5 \leftrightarrow 4\) 所以 \(4\) 号点的度为 \(4\)。

边/点权

边权：可以理解为走这条边的花费。

点权：可以理解为走到这个点的花费。

下图每一条边的边权都是 \(7\)。

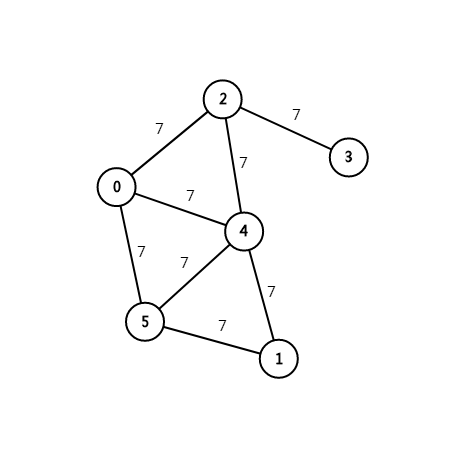
连通

连通：如果从 \(u\) 号点可以走到 \(v\) 号点就称 \(u\) 和 \(v\) 连通。

下图左 \(2\) 和 \(5\) 是连通的， \(2\) 和 \(1\) 是不连通的。

下图右 \(2\) 和 \(5\) 是连通的， \(2\) 和 \(1\) 也是连通的。

强连通

强连通：如果从 \(u\) 号点可以走到 \(v\) 号点，从 \(v\) 号点可以走到 \(u\) 号点，就称 \(u\) 和 \(v\) 强连通。

环

环：从 \(u\) 又走回了 \(u\)，你所走的路径构成了环。

如下图中 \(1 \rightarrow 5\)、\(5 \rightarrow 4\)、\(4 \rightarrow 1\) 构成了一个环。

连通图

连通图：图中任意两点都连通的图叫做连通图。

完全图

完全图：在不计算边权的情况下，不能再连边的图（没有两个点之间没有边了）。

如下图就是一个完全图。

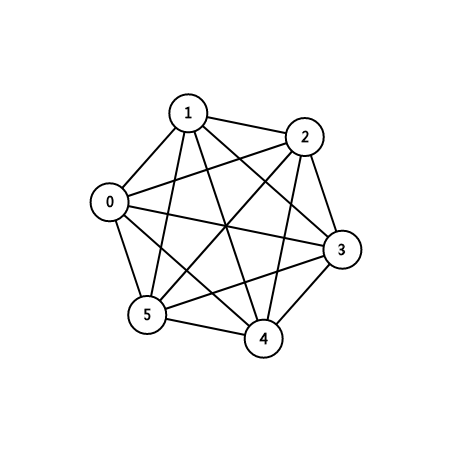
如果一个无向图是完全图，那么有 \(\frac{n \times (n-1)}{2}\) 条边，\(n\) 是顶点个数。第一个点可以和其他 \(n - 1\) 个点连边，第二个点可以和其他 \(n - 2\) 个点连边，因为第一个点和它连过了，其他点类似。所以最后的边数是 $ 1 + 2 + 3 + ... + n - 1 $，等差数列求和公式 \(\frac{n \times (n-1)}{2}\) 。

如果一个有向图是完全图，每个点都可以连出去 \(n-1\) 条边，所以边数为 $ n \times (n-1)$。

百度百科上说完全图是无向图，但一本通上既说了无向图，也说了有向图，咱也不知道，咱也不敢问。

然而，完全图的绘图，其顶点放置在正多边形的点上，已经在13世纪中出现。这样的绘画有时被称为神秘玫瑰。

bb多了，应该只bb定义的

稠密/稀疏图

稠密图：边数接近完全图的图，总而言之，就是边很多。

稀疏图：边数远少于完全图的图，总而言之，就是边很少。

不算基础吧

顶点集合

顶点集合：是原图中点的集合（任意几个点都可以）。

割点集合

割点集合：是个顶点集合，在原连通图中删去集合中的所有的点和与集合中的点相连的边后，原连通图不再连通。

点连通度

点连通度：最小的割点集合的大小（最小的割点集合中的点的个数）。

割边集合

割边集合：是个边的集合，在原连通图中删去集合中所有的边后，原连通图不再连通。

边连通度

边连通度：最小的割边集合的大小（最小的割边集合中边的个数）。

割点

割点：一个点，使得在原连通图中删去该点后原连通图不再连通，很明显只有当该图的点连通度为 \(1\) 时，该图才存在割点。