数据预处理——数据离散化

离散化，对数据做逻辑分层
1. 什么是数据离散化？
  所谓离散化，就是把无限空间中有限的个体映射到有限的空间中。数据离散化操作大多是针对连续数据进行的，处理之后的数据值域分布将从连续属性变为离散属性，这种属性一般包含2个或2个以上的值域。

2. 为什么要将数据离散化
节约计算资源，提高计算效率
算法模型的计算需要。虽然很多模型，例如决策树可以支持输入连续型数据，但是决策树本身会先将连续型数据转化为离散型数据，因此离散化转换是一个必要步骤。
增强模型的稳定性和准确度。数据离散化之后，处于异常状态的数据不会明显的突出异常特征，而是会被划分为一个子集中的一部分。如10000为异常值，可以划分为>100。因此异常数据对模型的影响会大大降低，尤其是基于距离计算的模型效果更明显。
特定数据处理和分析的必要步骤，尤其是在图像处理方面应用广泛。大多数图像做特征检测时，都需要先将 图像做二值化处理，二值化也是离散化的一种。
模型结果应用和部署的需要。如果原始数据的值域分布过多，或者值域划分不符合业务逻辑，俺么模型结果将很难被业务理解并应用。以银行信用卡评分距离，在用户填写表单时，不可能填写年收入为某个具体数字如100万，而是填写薪资位于哪个范围，这样从业务上来说才是可行的。
3. 如何将数据离散化？
3.1 时间数据离散化
  针对时间数据的离散化主要用于以时间为主要特征的数据集中和粒度转换，离散化处理后将分散的时间特征转为更高层次的时间特征。
  在带有时间的数据集中，时间可能作为行记录的序列，也可能作为列记录数据特征。常见的针对时间数据的离散化操作有以下两类：

针对一天中的时间离散化。一般是将时间戳转换为秒、分钟、小时或上下午。
针对日粒度以上数据的离散化。一般是将日期转化为周数、周几、月、工作日或者休息日
  针对时间数据的离散化可以将细粒度的时间序列数据离散化为粗粒度的3类数据：

离散化为分类数据，例如上午，下午
离散化为顺序数据，例如周一、周二、周三等
离散化为数值型数据，例如一年有52个周，周数是数值型数据
代码实现：

[1]:import pandas as pd 
    from sklearn.cluster import KMeans
    from sklearn import preprocessing
[2]:df = pd.read_csv("data.txt",sep='\t',names=['id','amount','income','datetime','age'])

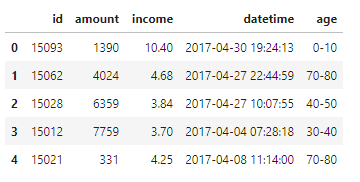
[4]:df['datetime'] = pd.to_datetime(df['datetime'])
    df["weekday"] = [i.weekday() for i in df["datetime"]]

 

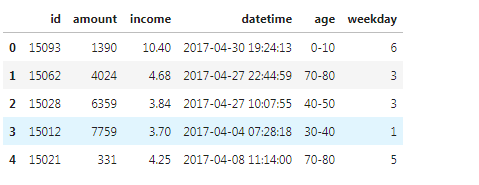
3.2 多值离散数据离散化
  针对多值离散数据的离散化指的是要进行离散化处理的数据本身不是数值型数据，而是分类或顺序数据。

  多值离散数据要进行离散化还有可能是划分的逻辑有问题，这一般是由业务逻辑影响的。例如，用户价值原来为高价值、中价值、低价值，现在要变为高价值、中价值、低价值和负价值。此时就需要对不同类别的数据进行统一规则的离散化处理。

代码实现：

[6]:map_df = pd.DataFrame(
        [['0-10', '0-40'], ['10-20', '0-40'], ['20-30', '0-40'], ['30-40', '0-40'], ['40-50', '40-80'],
         ['50-60', '40-80'], ['60-70', '40-80'], ['70-80', '40-80'], ['80-90', '>80'], ['>90', '>80']],columns=['age', 'age2'])  # 定义一个要转换的新区间
    df_tmp = df.merge(map_df, left_on='age', right_on='age', how='inner')  # 数据框关联匹配
    df_tmp.head()

 

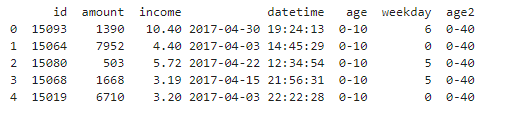
3.3 连续数据离散化
  针对连续数据的离散化是主要的离散化应用，在分类或关联分析中应用尤其广泛。这些算法的结果易类别或属性标识为基础，而非数值标记。
  连续数据的离散化结果可以分为两类：

将连续数据划分为特定区间的集合，例如将年龄分为(0,10]，(10,20]，(20,30]，(30,40]，(40,50]，(50,60]，(60,70]，(70,80]，(80,90]，(90,100]，(>100）.
将连续数据划分为特定类，例如将期末成绩评分分为Class_A,Class_B,Class_C
常见实现针对连续数据离散化的方法如下：

分位数法：使用四分位、五分位、十分位等分位数进行离散化处理，这种方法简单易行。
距离区间法：使用等距区间或自定义区间的方式进行离散化。这种方法比较领回，并且可以较好的保持数据原有结构分布。
频率区间法：将数据按照不同数据的频率分布进行排序，然后按照等频率或指定频率离散化，这种方法会把数据变换成均匀分布，但是会改变原有数据结果分布
聚类法：
卡方过滤：通过基于卡方的离散化方法，找出数据的最佳临近区间并合并，形成较大的区间
代码实现：
方法一：自定义区间分箱离散化

  首先确定特征最大值和最小值,确定我们分箱的最大和最小值。

 

[7]:df["amount"].max()
7952

[8]:df["amount"].min()
176

 

  自定义分箱区间

[9]:bins = [0,500,1000,2000,5000,10000]

 

  按照定义好的区间匹配数值

[10]:df.head()

 

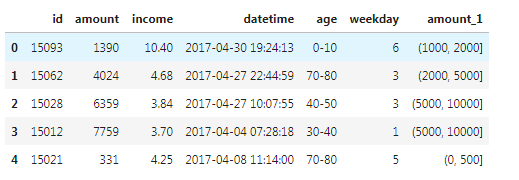
方法二：KMeans聚类离散化
  这里需要注意要将需要离散化的数据进行维度转化。因为直接用特征名取出的值是一维数据。而大部分算法模型要求必须是二维及以上的数据。

[11]:KMeans_model = KMeans(n_clusters=5,random_state=0)
     df["amount_2"] = KMeans_model.fit_predict(df["amount"].values.reshape(df["amount"].shape[0],1))
     df.head()

 

 

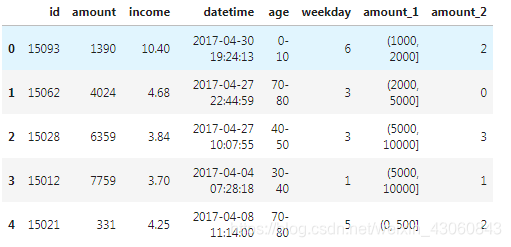
方法三：分位数法离散化
  这里以四分位举例，根据实际情况确定要以四分位，五分位还是十分位离散数据。

     df.head()

 

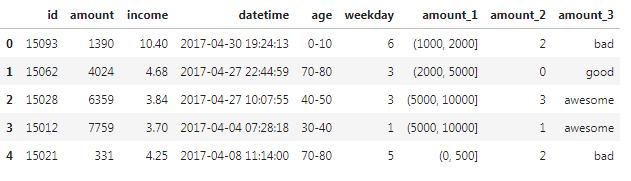
3.4 连续数据二值化
  在很多场景下，我们可能需要将变量特征进行二值化操作：每个数据点和阈值进行比较，大于阈值设置为某一固定值(例如1)，小于阈值设置为某一固定值(例如0)，然后得到一个只拥有两个值域的二值化数据集。

  二值化的前提是数据集中所有的属性值所代表的的含义相同或类似，例如读取图像所获得的数据集是颜色值的集合，因此每一个数据点都代表颜色，此时可对整体数据做二值化处理。

代码实现：

[13]:binarizer_scaler = preprocessing.Binarizer(threshold=df['income'].mean())  # 建立Binarizer模型对象
     income_tmp = binarizer_scaler.fit_transform(df[['income']])  # Binarizer标准化转换
     income_tmp.resize(df['income'].shape)  # 转换数据形状
     df['income_1'] = income_tmp  # Binarizer标准化转换
     df.head()

 

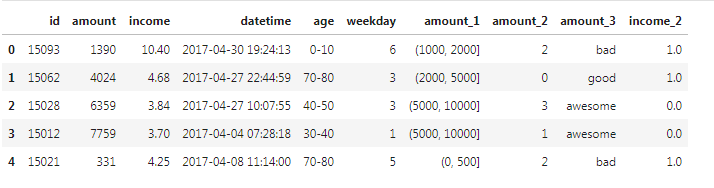
参考资料：《Python数据分析与数据化运营》
原文链接：https://blog.csdn.net/weixin_43060843/article/details/106351639