线段树学习

最近在学线段树，写个总结吧

定义

线段树，顾名思义，就是 以线段(区间) 为结点的树

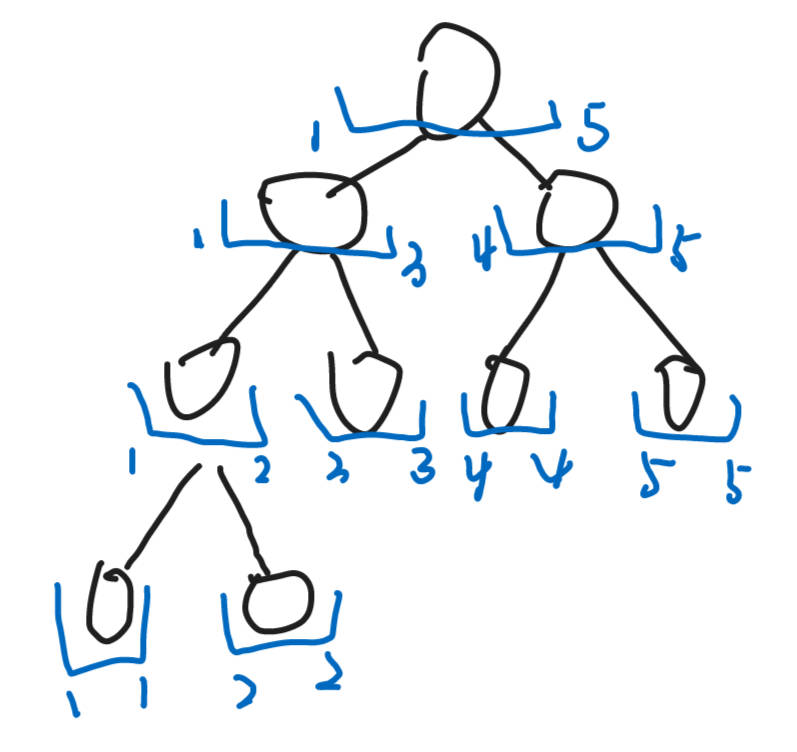
对于一个整区间 1~n，我们用一棵线段树来表示，任意一个节点储存某一区间内所有元素的和

根节点表示(1~n)，则左儿子表示区间（1，$\frac{n+1}{2}$），右儿子表示区间（$\frac{n+1}{2}+1$，n），本质上是对一个区间进行无限二分的过程，直到每个节点中只有一个元素（即到达叶节点）停止，每个节点将作为一个单独的值储存在数组的一格中

这样，在处理区间更新，区间求和等问题时，暴力求解为 $O(n)$，如果使用线段树，复杂度可以近似 $O(\log n)$

！！！ 若一个区间内元素数量为N，则由其生成的线段树最多会有 4N 个节点 (注意开数组大小

实践

建树

前言说过，线段树本质上是通过二分达到$O(\log n)$的复杂度

那么建树的时候，只要递归进行二分就可以，直到到达叶子节点就停止，在回溯过程中进行值的维护（有点像动态规划

int s[10000];   // 线段树数组
int a[10000];   // 原始数列数组
 
void buildtree(int x,int l,int r){  // 建树
// x 当前节点在数组中下标  l 当前节点代表区间的左边界  r 当前节点代表区间的右边界
    if(l==r){  // 到达叶节点
        s[x]=a[l];  // 更新值
        return;  // 叶节点无法继续递归，直接return掉
    }
    int mid=(l+r)>>1;
    buildtree(x<<1,l,mid);  // 左半边（注意左儿子包含中点
    buildtree(x<<1|1,mid+1,r);  // 右半边
    s[x]=s[x<<1]+s[x<<1|1];  // 值的维护
    // 可以用位运算稍稍优化，其实没什么影响
}

单点 / 区间查询

线段树对于单点上的操作其实总是更麻烦一些，但对于区间来说就要简单了

单点查询

我们知道，线段树为每个独立元素都找好了家（既有一个人的家，也包括他的所有祖宗），他把区间分割成很多部分，最小为单个元素，那么在线段树内查找单个元素，只要从根节点向下递归，直至找到目标元素所在叶节点

递归时，对于目标元素所属区间进行判断，若属于左儿子所代表的区间，则递归至左儿子区间，反之，递归至右儿子区间

int check(int x,int l,int r,int k,int w){
// x 当前下标  l 当前左边界   r 当前右边界  k 目标节点下标  w 更新值
	if(l==r) return s[x];// 找到叶节点，直接返回
	int mid=l+((r-l)>>1);  // 开始写二分
	if(k<=mid) check(x<<1,l,mid,k,w);  // 如果在左儿子（注意左儿子包括中点
	if(k>mid) check(x<<1|1,mid+1,r,k,w);  // 如果在右儿子
}

区间查询 ——> 区间和 / 前缀和

区间查询对于线段树来说复杂度就要低了，因为线段树就是把区间堆起来 (bushi

区间查询可以解决区间和、前缀和等问题，只要更改目标区间就可以

在区间查询的时候，如果我们遇到了一个与目标区间完全重合的节点，那么直接返回这个节点储存的值

但现实中大多不会出正好重合的区间，所以我们要进行多种情况的判断

（如果当前区间与目标区间不完全重合

1. 目标区间完全处于左儿子 ==> 表现为右边界小于中点

1. 目标区间完全处于右儿子 ==> 表现为左边界大于中点

3. 目标区间横跨左儿子和右儿子 ==> else

int calc(int x,int l,int r,int s,int t){
    if(l==s&&r==t)  // 到目标区间
        return s[x];  // 直接返回
    int mid=(l+r)/2;
    if(t<=mid)  // 左
        return calc(x*2,l,mid,s,t);
    else if(s>mid)  // 右
        return calc(x*2+1,mid+1,r,s,t);
    else  // 跨
        return calc(x*2,l,mid,s,mid)+calc(x*2+1,mid+1,r,mid+1,t);
    // 记得分割目标区间，左边为 l~mid   右边为 mid+1~r
}

单点更新 (很简单

对于单点更新，其实 暴力 是更好的做法 ( 暴力 $O(1)$ , 线段树 $O(\log n)$），但主要是为了区间更新做准备

查询的过程和上面一样，因为是单点，更改就直接加就好了 qwq

void check(int x,int l,int r,int k,int w){
// x 当前下标  l 当前左边界   r 当前右边界  k 目标节点下标  w 更新值
	if(l==r){   // 找到叶节点
		s[x]+=w;  // 单点更新 （ 确实很简单
		return;
	}
	int mid=l+((r-l)>>1);  // 开始写二分
	if(k<=mid) check(x<<1,l,mid,k,w);  // 如果在左儿子（注意左儿子包括中点
	if(k>mid) check(x<<1|1,mid+1,r,k,w);  // 如果在右儿子
	s[x]=s[x<<1]+s[x<<1|1];  // 更新之后需要维护，来确保正确性
}

区间更新