7-23 小测
本人小测分:100+100+10+0=210( ̄ー ̄)
由于本人比较菜,所以本人将自己写的题解和我老师给的题解放在一起帮助各位学习
第1题 妙妙咒语
在迪斯尼乐园里,有 N 个米奇妙妙屋,编号为 1 到 N。
第 i 个妙妙屋位于坐标 (x_i, y_i),且所有妙妙屋的坐标都不相同。
米奇妙妙屋之间可以用传送咒语来移动。
每种咒语由一个整数对 (a, b) 标识,对坐标 (x, y) 施放咒语 (a, b) 会将你传送到 (x+a, y+b)。
魔术师 kkkw 可以学习任意多的咒语,数量不限。
为了能够在任意两座妙妙屋之间旅行,他希望学习尽量少的咒语,使得对于任意一对不同的妙
妙屋 (i, j),都能选择一种已学的咒语 (a, b),通过多次使用(可以是负次数)该咒语,从 i 号屋移动到 j 号屋。
请问他至少需要学习多少个不同的咒语,才能达到目的?
输入格式
第一行一个整数 N,表示米奇妙妙屋的数量。
接下来 N 行,每行两个整数 x_i, y_i,表示第 i 个妙妙屋的坐标。
输出格式
输出一个整数,表示最少需要学习的咒语数量。
思路:

本题是一道暴力的题 (看代码就能懂),至于为什么要加gcd是因为,例:(0,0),(1,0),(2,0),从(0,0)到(1,0)要1,0,而从(0,0)到(2,0)也可以要1,0所以要加gcd。
代码:
#include<bits/stdc++.h>
using namespace std;
int n,x[505],y[505];
set<pair<int,int> >a;
int gcd(int a,int b)
{
if(b)return gcd(b,a%b);
else return a;
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%d%d",&x[i],&y[i]);
}
for(int i=1;i<n;i++)
{
for(int j=i+1;j<=n;j++)
{
int xx=x[j]-x[i],yy=y[j]-y[i],g=gcd(xx,yy);
if(g!=0)
{
xx=xx/g;
yy=yy/g;
}
a.insert({xx,yy});
}
}
printf("%d",a.size()*2);
return 0;
}
第2题 木雕玩具
在一个小镇上,有一个专门从事木雕工艺的工作室,只有三位雕刻师在那里工作。
小镇计划举办一个木制玩具节,届时将有 n 个人来到工作室请求制作木制玩具。
每个人想要的玩具图案都不一样,用 a_i 表示第 i 个人想要的图案。
每位雕刻师可以事先选择一个图案(用 1 到 10^9 之间的整数 x 表示),
不同雕刻师选择的图案可以不同。雕刻师能立即制作自己选定图案的玩具。如果要制作别的图案 y,则需要 |x-y| 的时间。
在玩具节当天,每个人请求制作玩具时,可以由任意一位雕刻师制作,雕刻师可以同时为不同的人工作。
员工们希望选择各自准备的图案,使得所有人中等待时间最长的那个人尽可能小。请你求出这个最小的最大等待时间。
输入格式
第一行一个整数 n,表示来工作室的人数。
第二行 n 个整数 a_1 到 a_n,表示每个人想要的玩具图案。
输出格式
输出一个整数,表示所有人最大等待时间的最小可能值。
思路:

由“使得所有人中等待时间最长的那个人尽可能小”,我们可以想到二分答案。
代码:
#include<bits/stdc++.h>
using namespace std;
int n,a[200005],y=-1;
bool d(int x)
{
int a1=upper_bound(a+1,a+1+n,a[1]+x*2)-a;
if(a1>n)return 1;
int a2=upper_bound(a+1,a+1+n,a[a1]+x*2)-a;
if(a2>n)return 1;
int a3=upper_bound(a+1,a+1+n,a[a2]+x*2)-a;
if(a3>n)return 1;
return 0;
}
int main(){
scanf("%d",&n);
int l=0,r=1000000000,mid;
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
}
if(n<=3)
{
printf("0");
return 0;
}
sort(a+1,a+1+n);
while(l<=r)
{
mid=(l+r)/2;
if(d(mid))
{
y=mid;
r=mid-1;
}
else
{
l=mid+1;
}
}
printf("%d",y);
return 0;
}
第3题 枢纽

输入格式

输出格式

思路:
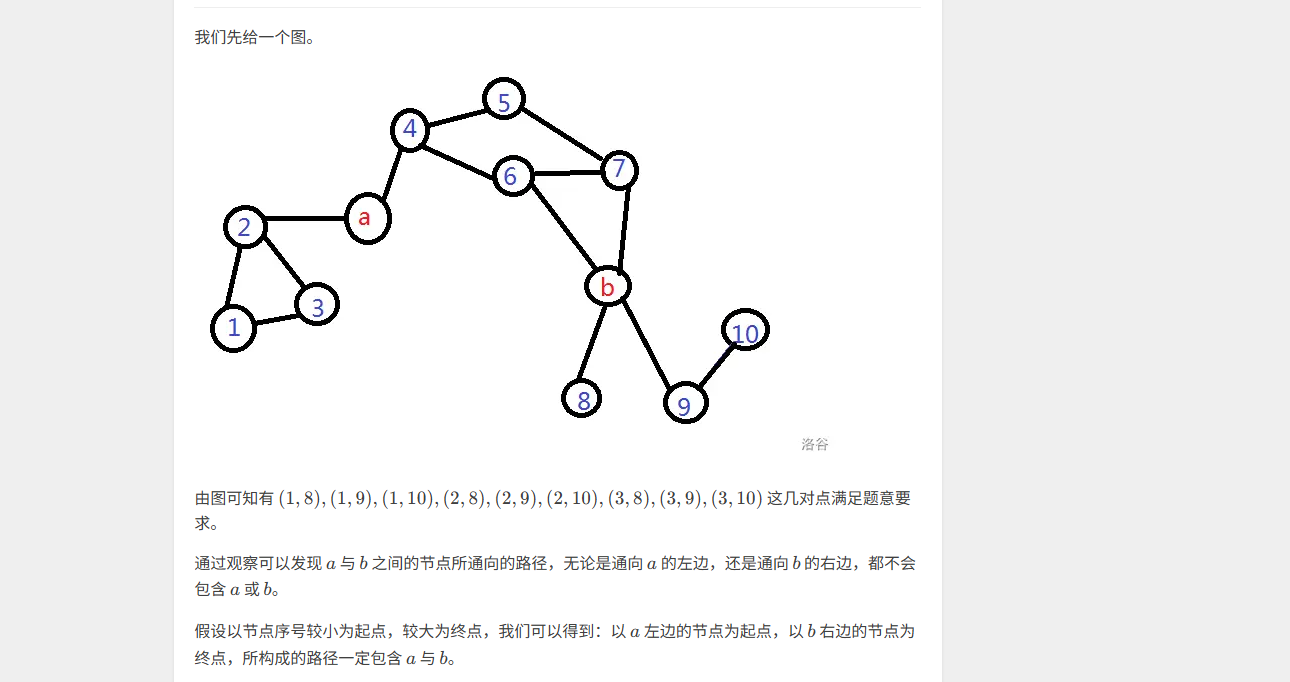
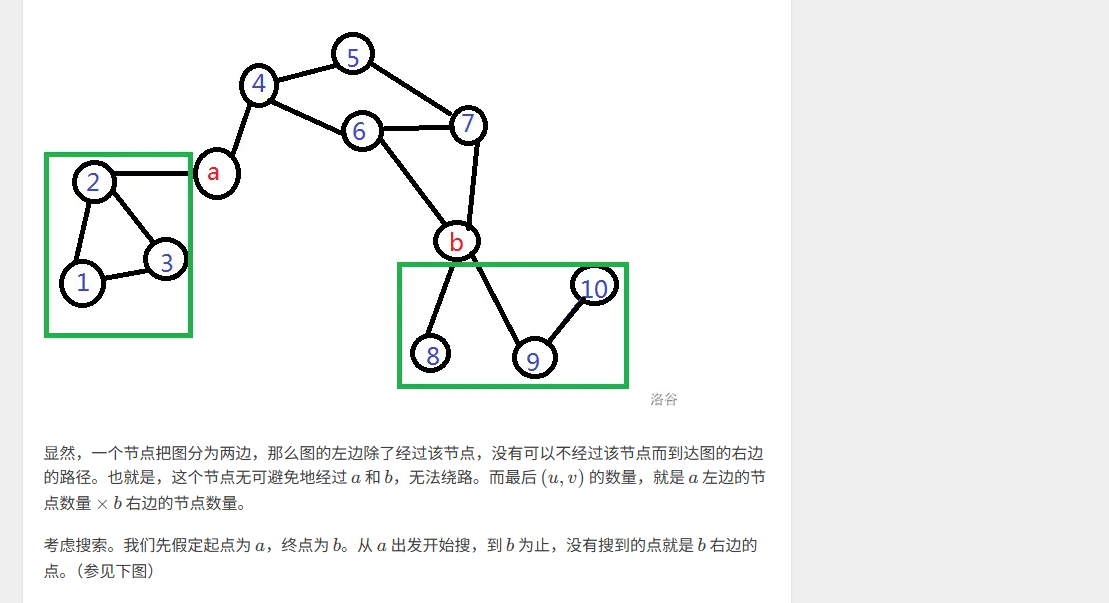
我们可以想到如果(u,v)存在那么这个图一定分为三大坨。
1.a可以到达的点,b不可以到达的点
2.a可以到达的点,b也可以到达的点
3.a不可以到达的点,b可以到达的点
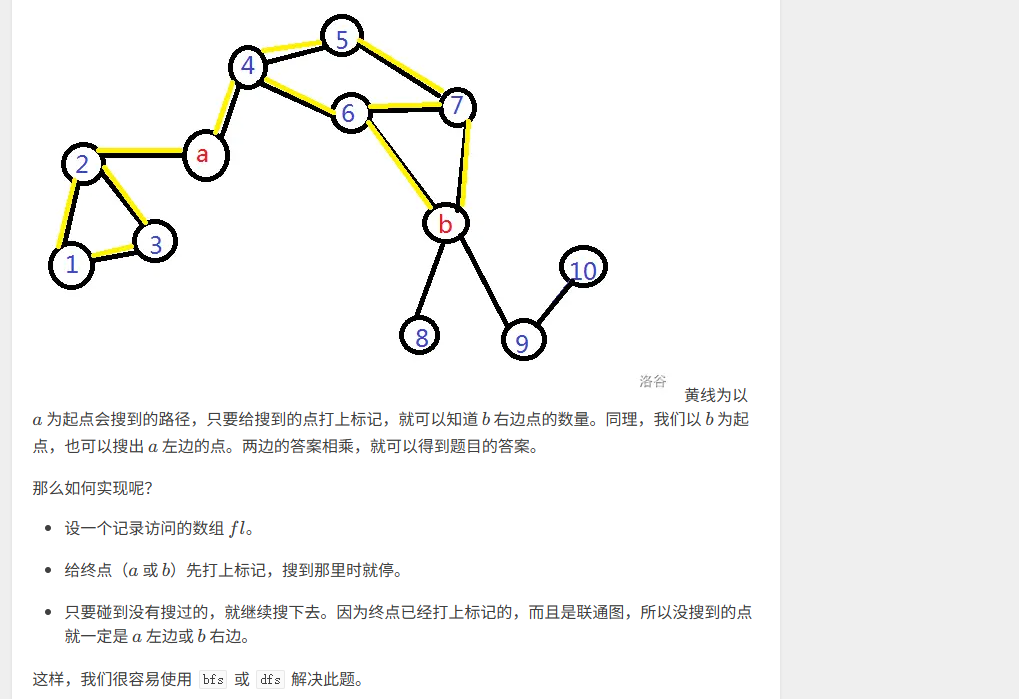
我们画图可知答案是(第一坨的点数)×(第三坨的点数)
而如果(u,v)不存在就不会分三大坨。
代码:
#include<bits/stdc++.h>
using namespace std;
int n,m,a,b;
vector<int>a1[200005];
bool v[200005];
void dfs(int x)
{
v[x]=1;
for(int i=0;i<a1[x].size();i++)
{
if(v[a1[x][i]]==0)
{
v[a1[x][i]]=1;
dfs(a1[x][i]);
}
}
}
int main(){
scanf("%d%d%d%d",&n,&m,&a,&b);
for(int i=1;i<=m;i++)
{
int u,v;
scanf("%d%d",&u,&v);
a1[u].push_back(v);
a1[v].push_back(u);
}
long long s1=0,s2=0;
v[b]=1;
dfs(a);
for(int i=1;i<=n;i++)
{
if(v[i]==0)
{
s1++;
}
v[i]=0;
}
v[a]=1;
dfs(b);
for(int i=1;i<=n;i++)
{
if(v[i]==0)
{
s2++;
}
}
printf("%lld",s1*s2);
return 0;
}
第4题 魔法药水
你是“北国”的国家炼金术师,拥有超高的魔法造诣。
现在面前有 n 种材料,第 i 种材料的魔力为 a_i。
你要从这些材料中选择一种或多种混合,制作一种药水。
混合 k 种材料时,药水每单位时间的魔力会增加 k。药水的初始魔力值等于所选材料的魔力和。
你会在 0 时刻把所有材料一次性混合好。之后不会再添加材料。
你想知道,最早在第几时刻,药水魔力值能正好达到 m?
输入格式
第一行包含两个整数 n, m,分别表示材料数量和目标魔力值。
第二行包含 n 个整数 a_1 ~ a_n,表示每种材料的魔力值。
输出格式
输出一个整数,表示最早能获得魔力正好为 m 的药水的时间。
思路:

我们知道m很大所以我们无法开贼么大的数组,于是我们发现"m%k==sum%k"(sum为药水的初始魔力值)。
若想要到达m的时间最短,那么在固定k的情况下,一定是cum最大最好。因此我们枚举k,定义dp[i][j][k]表示前i个材料中选j个材料余数为k时sum的最大值。
代码:
#include <bits/stdc++.h>
using namespace std;
int n;
long long m,a[105],dp[105][105][105],y=LLONG_MAX;
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++)
{
cin>>a[i];
}
for(int k=1;k<=n;k++)
{
int mod=k;
memset(dp,-1,sizeof(dp));
dp[0][0][0]=0;
for(int j=1;j<=n;j++)
{
for(int l=0;l<=k;l++)
{
for(int r=0;r<mod;r++)
{
dp[j][l][r]=dp[j-1][l][r];
if(l>0)
{
if(dp[j-1][l-1][(r-(a[j]%mod)+mod)%mod]!=-1)
{
if(dp[j][l][r]<dp[j-1][l-1][(r-(a[j]%mod)+mod)%mod]+a[j])
{
dp[j][l][r]=dp[j-1][l-1][(r-(a[j]%mod)+mod)%mod]+a[j];
}
}
}
}
}
}
if(dp[n][k][m%mod]!=-1&&dp[n][k][m%mod]<=m)
{
long long t=(m-dp[n][k][m%mod])/k;
if(t>=0&&t<y)
{
y=t;
}
}
}
cout<<y;
return 0;
}
欢迎大家在评论区开喷


 浙公网安备 33010602011771号
浙公网安备 33010602011771号