斯特林数学习

 摘自：

https://www.cnblogs.com/owenyu/p/6724661.html

https://en.wikipedia.org/wiki/Stirling_numbers_of_the_first_kind#cite_note-22

 https://blog.csdn.net/doyouseeman/article/details/50876786

https://blog.csdn.net/lyd_7_29/article/details/75041818

 

 　　　

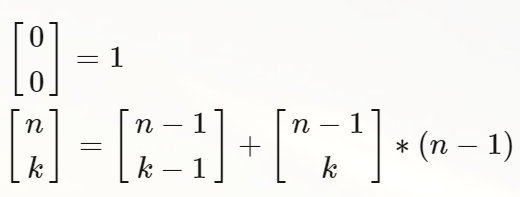
定义：（s(n,k)带符号）

　　　　　　　

  

符号说明：

 　　　　

　　　　　　

 

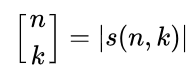
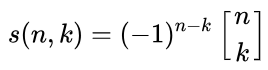
斯特林数跟下降上升阶乘幂有关：

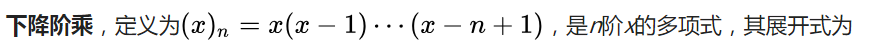
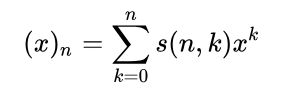
怎么来的？不好意思这个网上资料似乎还真没法直接构造原理证明，只能间接归纳法证明

因为，实质上维基百科上斯特林数的通项公式为：

 

 

 

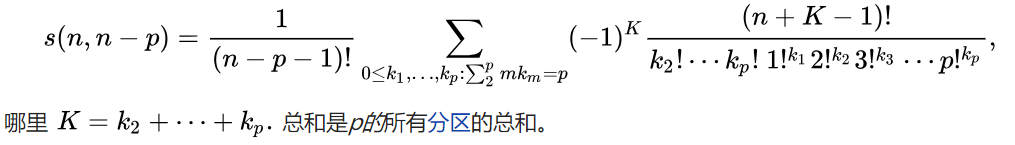
间接证明如下：

 

 

 

 另一方面，

下降阶乘就是排列数

　　

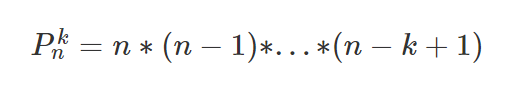
所以

       　　 

              　　    

 

 一个性质：

　　　　　　　　

证明：

 

　　　 

 

 
解决自然数幂和：

设：

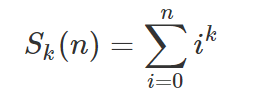
      且发现，

　　

 

 

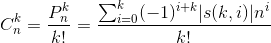
　　联想到求和的那个东西下降阶乘中斯特林表达式出现过，将i=k的n^k那一项提取出来：

 

    　　　　          

　　　　　　　　

　　　　　　　　

　　　　　　　　

 

 

 

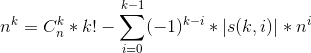
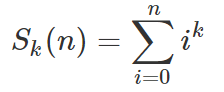
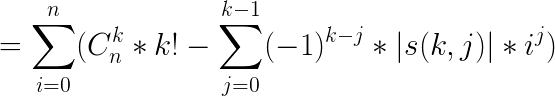
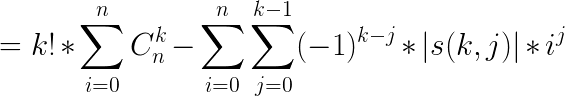
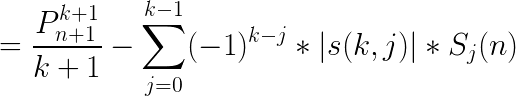
int get_sum(int n)
{
    sum[1]=(LL)n*(n+1)/2%MOD;
    for (int i=2;i<=k;i++)
    {
        sum[i]=1;
        for (int j=0;j<i+1;j++)
            if ((LL)(n-j+1)%(i+1)==0) sum[i]=(LL)(n-j+1)/(i+1)*sum[i]%MOD;
            else sum[i]=(LL)(n-j+1)*sum[i]%MOD;
        for (int j=1;j<i;j++)
            if ((i-j)%2==0) (sum[i]-=(LL)s[i][j]*sum[j]%MOD)%=MOD;
            else (sum[i]+=(LL)s[i][j]*sum[j]%MOD)%=MOD;
    }
    return (sum[k]+MOD)%MOD;
}

 

 

第一类Stirling数不同的是，第二类斯特林数集合内是不考虑次序的，而圆排列是有序的。 

 

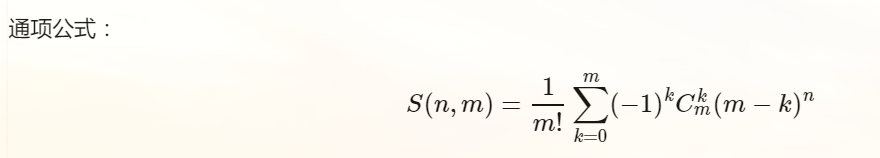
　　一个实例

 

 

百度百科都有证明

 

 

 

 

 

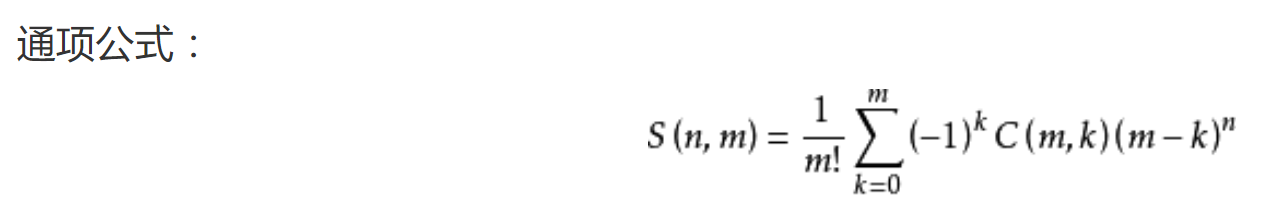
第二类斯特林数求自然数幂