力扣

1、如果需要考虑之前的状态就可以使用有限状态机

有限状态机：

 

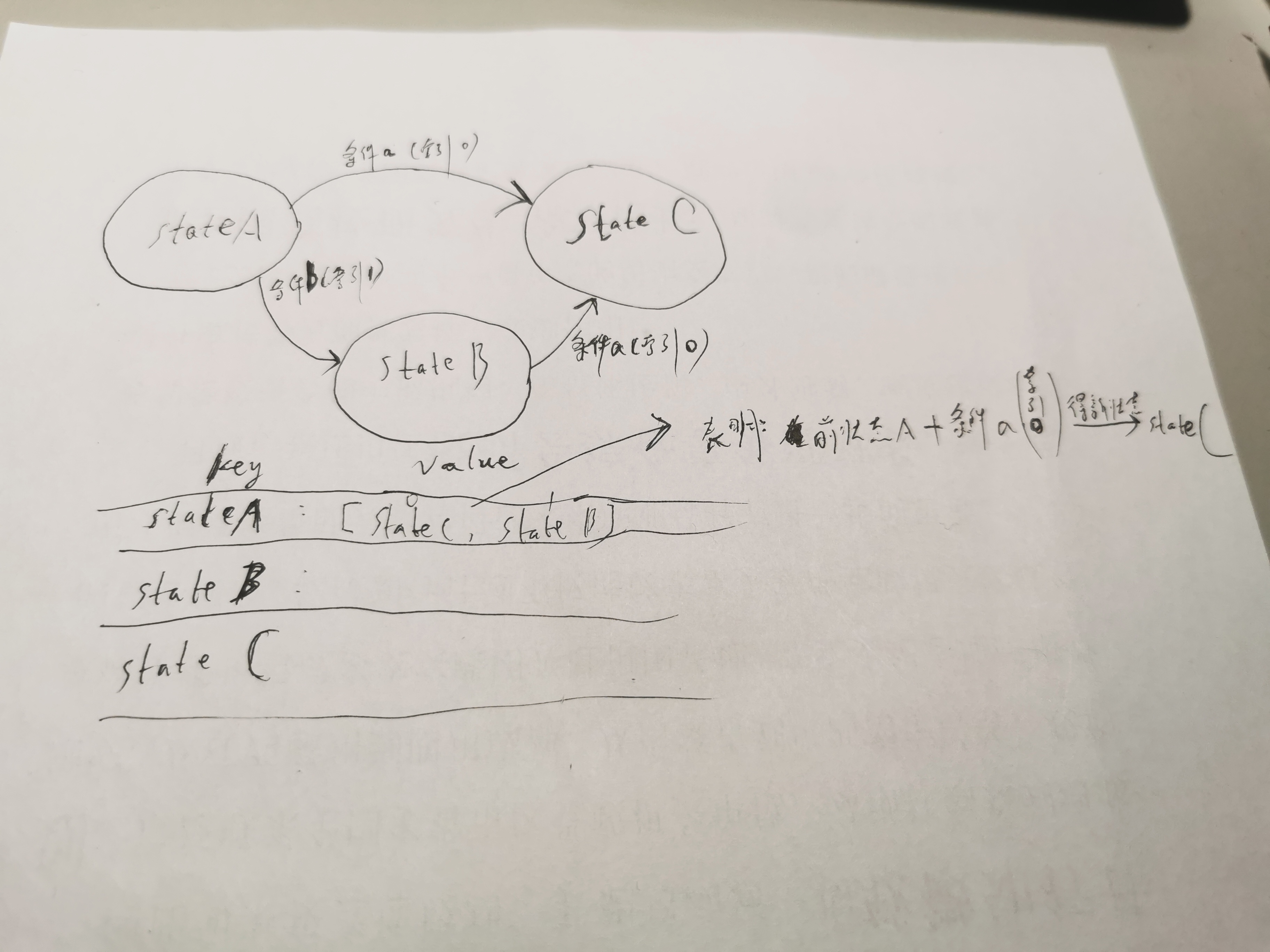
 Leecode 第8题：

 

 

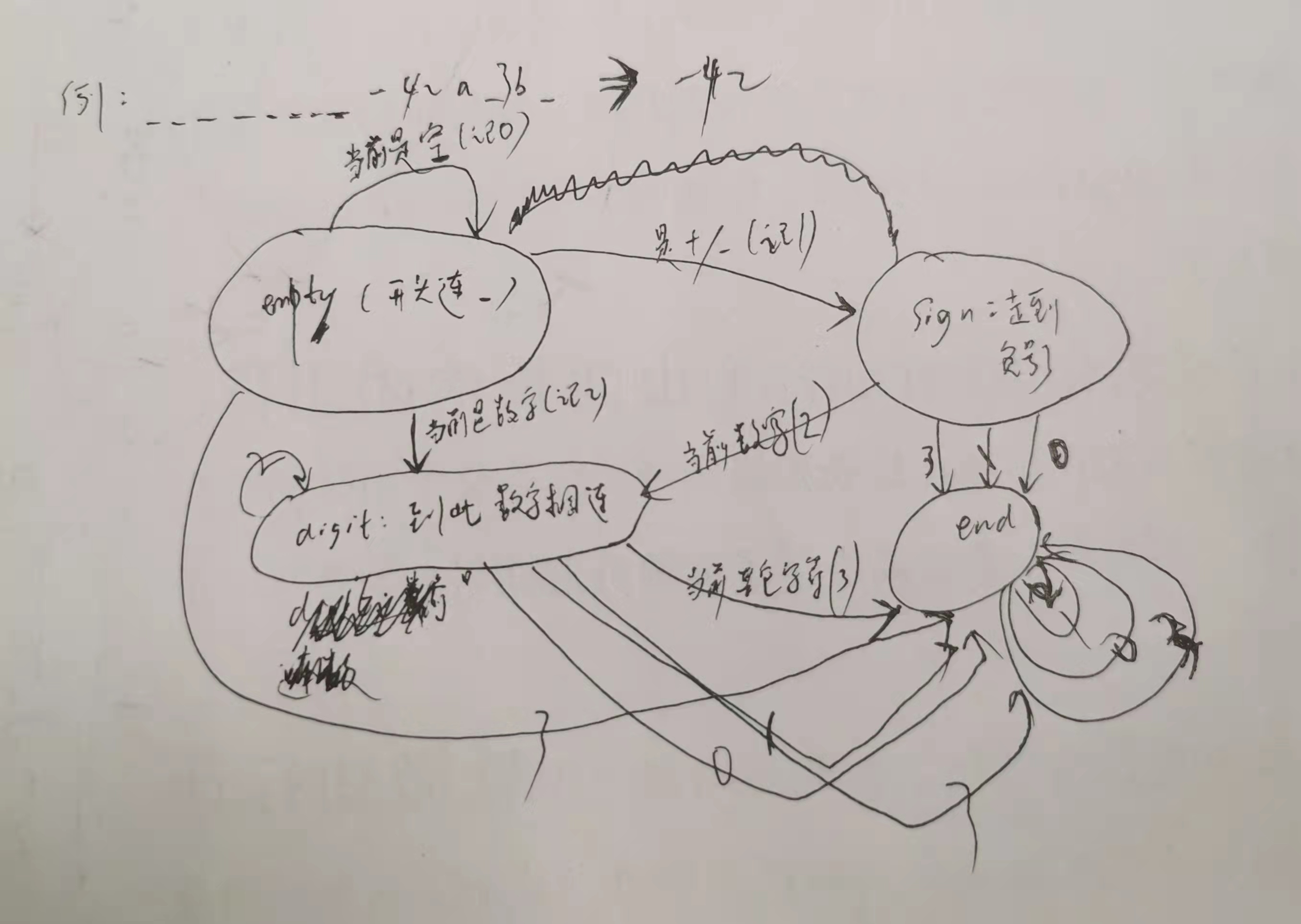
class A:
    def __init__(self):
        self.sign=1
        self.ans=0
        self.currentState="empty"
        self.dict={
            "empty":["empty","sign","digit","end"],
            "sign":["end","end","digit","end"],
            "digit":["end","end","digit","end"],
            "end":["end","end","end","end"]
        }
    def tocondition(self,s:str,i:int): # 条件转化为数字
        if s[i]==' ':
            return 0
        elif s[i]=='+' or s[i]=='-':
            return 1
        elif s[i].isdigit():
            return 2
        else:
            return 3
    def deal(self,s:str,i:int):
        condition = self.tocondition(s,i)
        self.currentState=self.dict[self.currentState][condition]
        if self.currentState=="sign":
            self.sign = -1 if s[i]=='-' else 1
        if self.currentState=='digit':
            self.ans=self.ans*10+int(s[i])

class Solution:
    def myAtoi(self, s: str) -> int:
        a = A()
        for i in range(len(s)):
            a.deal(s,i)
        res = a.sign * a.ans
        if res<-2**31:
            res=-2**31
        if res>2**31-1:
            res=2**31-1
        return res

 2、非递归先序遍历

准备一个栈，然后访问根节点，入栈，走到左子树，访问，入栈，左子树没了访问不了，出栈一个元素，走到它的右子树，访问根节点...直到访问不了且栈空了（想用刚刚的元素，就可以想到栈）

        stack = []
        while root or len(stack)!=0:
            if root:
                print(root.val)
                stack.append(root)
                root=root.left
            else:
                root = stack.pop()
                root = root.right

2、层次序列生成二叉树

对当前节点，给他左边加节点，然后入队，右边加节点，然后入队，出队一个元素，对该元素左边加节点...（想到用老之前的元素，就可以想到队列）

    def create(self,nums): # 层次建立二叉树
        root = Node(nums[0])
        q = queue.Queue(len(nums))
        q.put(root)
        i = 1
        while i<=len(nums):
            if nums[i]=='null':
                i+=1
                continue
            node = q.get()
            node.left = Node(nums[i])
            q.put(node.left)
            i+=1
            if i==len(nums):
                break
            if nums[i]=='null':
                i+=1
                continue
            node.right = Node(nums[i])
            q.put(node.right)
            i+=1
        return root

    def mid(self,root): # 非递归中序遍历
        stack = []
        while root or len(stack)!=0:
            if root:
                stack.append(root)
                root=root.left
            else:
                top = stack.pop()
                print(top.val)
                root = top.right

    def pre(self,root): # 非递归先序遍历
        stack = []
        while root or len(stack)!=0:
            if root:
                print(root.val)
                stack.append(root)
                root=root.left
            else:
                root = stack.pop()
                root = root.right

 3、01背包问题

一个背包总容量为V，现在有N个物品，第 i 个 物品体积为weight[i]，价值为value[i]，现在往背包里面装东西，怎么装能使背包的内物品价值最大？

思路：

1️⃣、考虑二元的递推公式能覆盖一元的

2️⃣、将物品一字排开，定义 f( i , n ) ： 只考虑前 i 件商品 & 背包容量为 n ，能装的最大价值

3️⃣、以后面一件是否放进包里考虑，得到 f (i , n ) = max (   f(i-1,n) , f( i-1 ,  n - 最后一件物品的容量) + 该物品的价值   ) 

 4、堆

建堆的时间复杂度为O(n)

调整堆的时间复杂度为 lgn，其中调用了n-1次，因此堆排序的时间复杂度为O(n)+O(nlgn) ~ O(nlgn)

大根堆就是根节点是整棵树的最大值(根节点大于等于左右子树的最大值)，对于他的任意子树，根节点也是最大值

堆排序可以取出前 top k 个元素，这 k 个也无需排序

python里是建立最小堆：heapify(列表)

添加元素，堆会自动调整：heappush(my_data,0.5)

弹出堆顶：heappop(my_data)

 5、异或运算x ^ y的性质

 

6、队列

queue.Queue(maxsize=2)
q.put(1)：入队

q.get()：出队

 7、求升序整数序列的最小的绝对值，要求复杂度在O(n)以下

1️⃣ 分情况简化问题，全正数、全负数，有正有负

2️⃣ 目标值肯定在正数和负数挨得最近的地方

3️⃣ 二分法一般有3个指针，左，中，右

 8、找一个字符串长度为k的字典序最小的子序列

1️⃣字符串qaqbqcq的字典序最小的子序列是abcq

2️⃣把字符串输入到单调递增队列中，能够得到字典序最小的子序列

3️⃣单调递增队列的队首元素是字符串中的字典序最小元素

4️⃣队首弹出后的结果是队首元素后面的字符串的字典序最小的子序列

 list.pop(index)：删除指定索引的元素

def inqueue(q,ele): # 往递增队列放一个元素
    while len(q)>0 and q[-1]>ele:
        q.pop()
    q.append(ele)

str="qaqbqcq"
res=""
k=3
count=0
q=[]
while count<len(str)-k: # 把前面的字符串入队
    inqueue(q,str[count])
    count+=1
for i in range(k): # 最后k个元素入队，每入一个就出队一个
    inqueue(q,str[len(str)-k+i])
    res+=q.pop(0)
res