算法系列1 初识算法 算法复杂性模型 算法复杂度的计算

算法系列1 初识算法

什么是算法？

定义：由若干条指令组成的有穷序列，且满足：输出输入，确定性，有限性
输入：有零个或多个由外部提供的量作为算法的输入
输出：算法产生至少一个量作为算法的输出
确定性：组成算法的每条指令是清晰的，无歧义的
有限性：执行每条指令的时间是有限的，执行的次数也是有限的

D.E.Knuth（高德纳）在他的专著程序的设计的艺术中给出了一个算法的定义是目前学术界比较认可的，
定义如下：算法是定义一个可终止的有序的，无歧义的，可执行的步骤的集合

要成为金字塔顶的程序员，算法是我们取经之路上必不可少的，让我们一起打开算法的大门，
互相监督，共同进步，我将会在我的个人博客更新我的算法系列文章。

算法与程序的区别

算法是计算机科学的核心，是指解决问题的结构化流程，是编排计算机指令的策略性步骤，算法是与语言无关的。即算法不依赖于什么样的程序设计方法，更不依赖于具体的编程语言
算法：一种语言
程序：一种文本
算法：受专利法保护
程序：受著作法保护

一些算法的名称

我也会逐一学习这些算法，共勉

我们既然要学算法，那么自然要学怎么判断一个算法的高效性，即什么算法能让我们的程序跑的更快，占用的内存更小。这就要学习算法的复杂度模型

算法的复杂度模型

复杂性的问题规模N，输入I和算法A的函数
T=T(N，I,A)
问题规模N没有明确的单位。T也没有明确的单位，一个输入I对应一个问题的实例
判断一个算法的高效与否不能仅仅看一个算法运行速度的快慢，还要看看一个算法占用内存的多少，这就有了时间复杂度与空间复杂度

我先来讲讲没有学习计算算法的复杂度之前，我是怎么来判断一个算法的高效与否的，我相信这也是大多数人的错误
我当初认为评价一个算法的执行效率无非就是给出一组数据，用不同的算法进行运算，这种方法也叫事后统计法，但是这种方法是有很明显的缺点的

缺点

1.执行时间严重依赖硬件以及运行时各种不确定的环境因素
2.必须编写相应的测试代码，比较麻烦
3.测试数据的选择比较难保证公平公正，这句话的意思就是可能不同算法对不同数据的处理效率不
比如有两个算法，两组数据，当输入数据1的时候算法1的效率更高，当输入数据2的时候算法二的效率跟高

我们一般使用以下纬度来评估算法的优劣：正确性，健壮性，可读性
时间复杂度：估算程序指令的执行次数
空间复杂度：估计所需要占用的内存

算法复杂性模型

复杂性是问题规模N,输入I,和算法A的函数
T=T(N,I,A)
问题规模N没有明确的单位
T也没有明确的单位
一个输入I对应一个问题实例

对特定的算法我们可以把A省略，得到T=T(A,I);
计算机有k种运算O1,O2……Ok。各有其执行的时间ti；
针对具体问题只取主要的运算Om为度量单位
例如：只涉及四则运算，取乘除问题为主要运算，对排序问题，取比较操作为主要运算

最坏情况，最好情况，平均情况

最坏情况Tmax= Tmax (N)=max[I]{T(N,I)}
最好情况Tmin = Tmin (N)= min[I]{T(N,I)}
平均情况Tavg = Tavg (N)= average[I]{T(N,I)}
各自的优点
最常用的是最坏情况时间复杂性

计算时间复杂度的例子

复杂性的渐进形态

算法复杂性的阶

进一步忽略系数的渐进性形态---------阶，阶有四种，上界阶,大O
定义
例如T(n)=2n-2k-1，其渐进形态为2n，省去系数后，其上界阶O(n)
下界阶，Ω
同级阶，θ
无穷小阶，小o

对阶记号的认识

大O表示法（Big O）n-1

一般使用大O表示法来描述复杂，他表示数据规模n对应的复杂度，忽略常数，系数，低阶

9 >> O(1)
2n+3 >> O(n)
n^2   +2n+6     >> O(n ^2)
n^3 +  3n ^2 +2n+6     >> O(n ^3)

大O表示法仅仅是一种粗略的分析模型，是一种估算，帮助我们短时间内了解一个算法的执行效率

对阶数的细节
对阶数一般省略底数
（图片来源小码哥）


为了让大家更直观的对比复杂度的大小我使用一个函数生成对比工具
（图片来源小码哥）

数据规模较小时

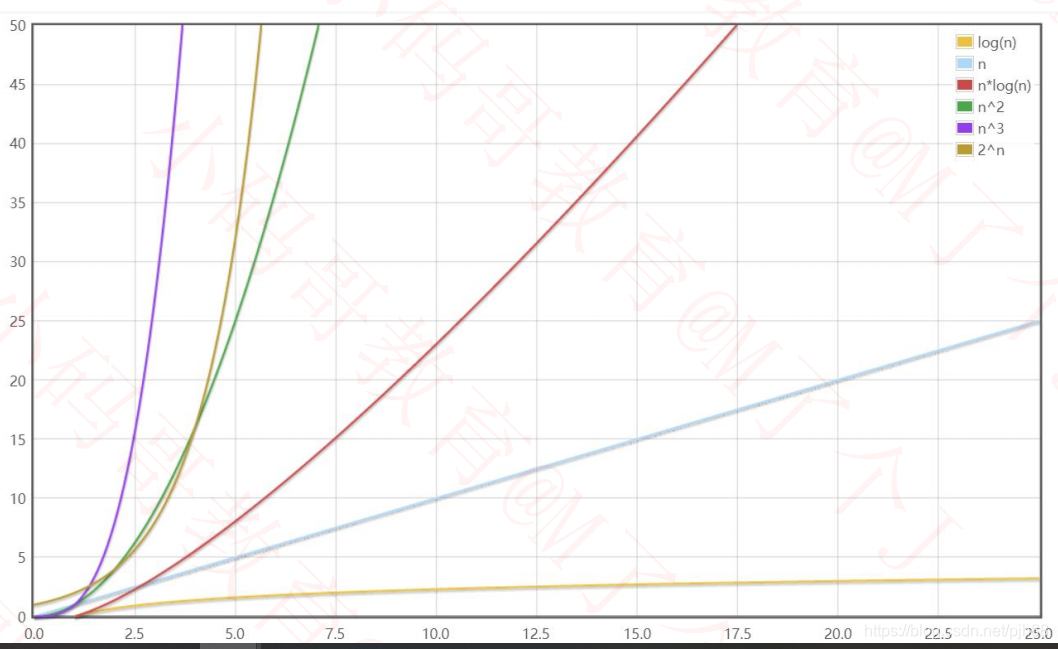
数据规模较大时

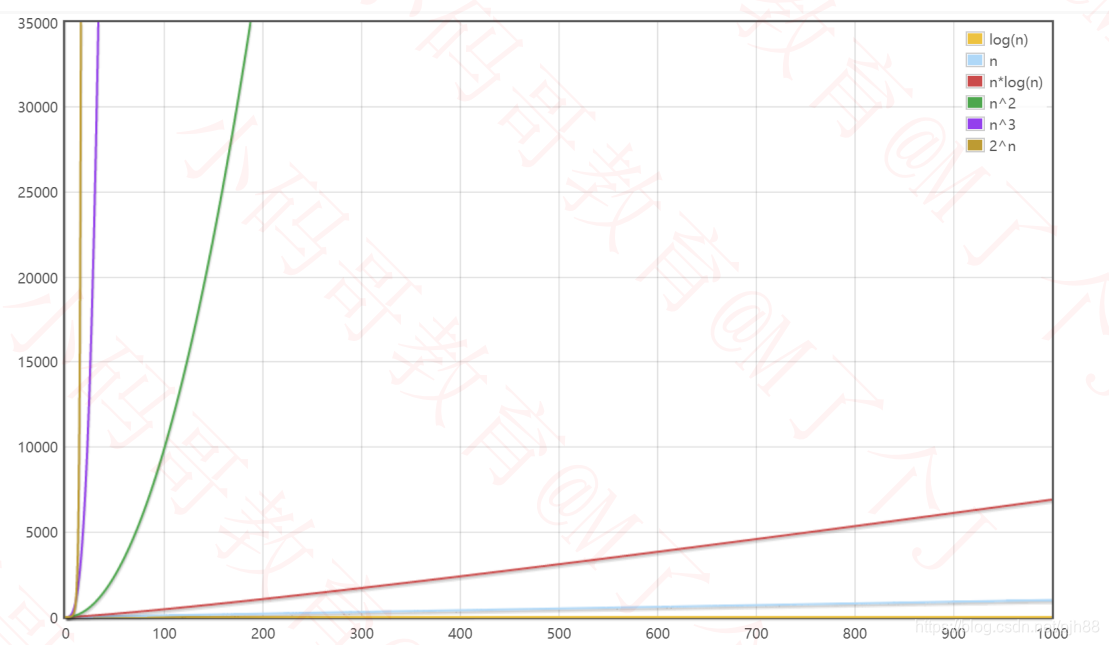
以上就是对算法复杂性计算的一些略微的总结，在后续学习过程中我会不断完善，欢迎大家关注我和我一同学习，一同进步