网络流学习笔记

注：笔者是蒟蒻，所以本文几乎是干货，枯燥无味~~甚至可能会引人不适，请读者谨慎阅读~~。

为了笔者快爆掉的肝点个赞好吗？？？

Part.1 网络流基础定义

一个有向带权图 $G=(V,E)$ 是一个网络当且仅当：

图中只有一个入度为 $0$ 的点，即源点 $S$；
图中只有一个出度为 $0$ 的点，即汇点 $T$；
每条边 $u\to v$ 的权值为正数，这个数表示此边的容量，记作 $c_{u,v}$。

网络流可以具象为流水的系统，源点就是水源，能无限的供应水，而汇点就是取水点，无限的消耗水，边就是管道，而且通过水的数量不能超过其容量。

形式化的讲，记在边 $u\to v$ 之间的流量为 $f_{u,v}$。若边在原图中存在，则会有如下性质：

$0<f_{u,v}\le g_{u,v}$；
$f_{u,v}=-f_{v,u}$；
对于一个点 $u$，和所有 $x\to u$ 的 $x$ 以及 $u\to y$ 的 $y$，有 $\sum\limits_{x} f_{x,u}=\sum\limits_{y} f_{u,y}$，这个性质被称作流量守恒（即流入多少水就流出多少水）。

增广路定义为一条从 $S$ 到 $T$ 剩余容量大于 $0$ 的路径。

残量网络定义为已经流过一些流量后删除满流的边的网络。

Part.2 最大流及其应用

模板题。

定义最大流为在满足上述性质的前提下，流入汇点的流量总和的最大值。重点在于如何求这个值。

首先有一个贪心，就是每次选择一个增广路，流出路径上的剩余流量的最小值，然后更新剩余流量。

上述算法显然是错误的，那我们如何补救呢？

考虑对于每个边建立反向边，初始的容量为 $0$。每次增广时，一条边容量减 $x$，其反向边容量加 $x$。结合下图理解：

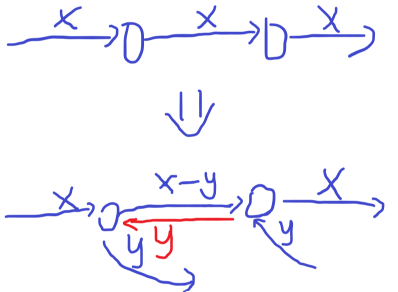
可以发现，建立反向边后，相当于给了一次撤销的机会，而上述假贪心加上这个优化过后就是对的了，笔者并不会证明。这个算法就是 FF 算法，时间复杂度与流量有关。

而每次选择源点到汇点的最短增广路进行增广，就得到了 EK 算法，时间复杂度 $O(nm^2)$。

每次只增广一条太亏了，所以把所有最短路径一起增广。具体的，以 $S$ 为起点对图 BFS，然后按距离分层，就只需要考虑相邻层之间的边了。从 $S$ 开始携带 $\infty$ 的流量向下遍历，每次枚举当前节点的邻居，尽量将手里的流量送出去。

注意到有效边组成的图一定是个 DAG，说明如果将一条边的剩余容量变成 $0$，这条边就不会再访问了。所以可以开个数组 $now_u$ 表示 $u$ 访问到那个邻居了，DFS 的时候就从 $now_u$ 开始遍历后面的边。

这个小优化叫做当前弧优化，加上这个优化的算法叫做 Dinic。其时间复杂度就降到了 $O(n^2m)$，而且跑不满（$n$ 开 $10^4$，$m$ 开 $10^5$ 都可以干过去），特别的，在二分图中，Dinic 的时间复杂度为 $O(m\sqrt n)$。这是 OI 中最常用的最大流算法。

放一下板子的代码：

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 2e2+5,M = 5e3+5;
int n,m,s,t,cnt = 1,head[N],to[M<<1],nxt[M<<1],g[M<<1];//cnt初始值为1方便获得反边 
inline void add(int x,int y,int z)
{
    nxt[++cnt] = head[x];
    head[x] = cnt;
    to[cnt] = y,g[cnt] = z;
}
int dis[N],now[N];
inline bool bfs()
{
    for(int i = 1;i<=n;i++) dis[i] = -1;
    queue<int> q;
    q.push(s);
    dis[s] = 0;
    now[s] = head[s];
    while(!q.empty())
    {
        int u = q.front();q.pop();
        for(int i = head[u];i;i = nxt[i])
        {
            int v = to[i];
            if(g[i]>0&&dis[v]==-1)
            {
                q.push(v);
                dis[v] = dis[u]+1,now[v] = head[v];
                if(v==t) return 1;
            }
        }
    }
    return 0;
}
int dfs(int u,int s)
{
    if(u==t) return s;
    int k,res = 0;
    for(int i = now[u];i;i = nxt[i])
    {
        if(!s) break;    
        int v = to[i];
        now[u] = i;//当前弧优化 
        if(g[i]>0&&dis[v]==dis[u]+1)//能流且位于下一层 
        {
            k = dfs(v,min(s,g[i]));
            if(k==0) dis[v] = 2e9;
            g[i]-=k,g[i^1]+=k,res+=k,s-=k;
        } 
    }
    return res;
}
signed main()
{
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    cin>>n>>m>>s>>t; 
    for(int i = 1,u,v,w;i<=m;i++)
        cin>>u>>v>>w,add(u,v,w),add(v,u,0);
    int ans = 0;
    while(bfs()) ans+=dfs(s,2e9);
    cout<<ans;
    return 0;
}

最大流的用处太多了，后文慢慢讲吧。

Part.3 费用流及其应用

模板题。

费用流其实就是在最大流上对于每个弧增加了一个属性：费用，每流过一个单位的流就会消耗对应的费用。让你求在流最大的情况下使得费用最少或最大。

先想想费用流中的反向边怎么建，其实就是正向边的费用和反向边的费用成相反数就行了。

那怎么增广呢？还记得最大流中的 EK 算法吗，这个算法在求最大流是不是寻找的最短的增广路吗，其实改到费用流里就每次把费用最少的增广路拿出来增广就行了（这里是求最小费用最大流）。然而由于图有负边权，所以只能跑 SPFA。

时间复杂度是 $O(nmf)$，其中 $f$ 指最大流。这个很容易理解，就是最多增广 $f$ 次，每次增广时瓶颈在于 SPFA，所以是 $O(nmf)$ 的。这个大大的跑不满，由于在题目中建出来的图比较特殊（最大流可能比较小），$n$ 开 $10^4$，$m$ 开 $10^5$ 都可以干过去。这就是名言“最大流不卡 Dinic，费用流不卡 EK”的由来。

放代码：

#include <bits/stdc++.h>
using namespace std;
const int N = 5e3+5,M = 1e5+5;
int n,m,s,t,cnt = 1,head[N],now[N],nxt[M],to[M],g[M],fl[M];
inline void add(int x,int y,int w,int flow)
{
    nxt[++cnt] = head[x];
    head[x] = cnt;
    to[cnt] = y,g[cnt] = w,fl[cnt] = flow;
    nxt[++cnt] = head[y];
    head[y] = cnt;
    to[cnt] = x,g[cnt] = -w,fl[cnt] = 0;
}
int dis[N],mn[N];
bool vis[N];
inline bool spfa()
{
    for(int i = 1;i<=n;i++)
        dis[i] = 2e9,vis[i] = 0;
    dis[s] = 0,mn[s] = 2e9,vis[s] = 1;
    queue<int> q;
    q.push(s);
    while(!q.empty())
    {
        int u = q.front();q.pop();
        vis[u] = 0;
        for(int i = head[u];i;i = nxt[i])
        {
            int v = to[i],w = g[i];
            if(fl[i]&&dis[v]>dis[u]+w)
            {
                now[v] = i,dis[v] = dis[u]+w,mn[v] = min(mn[u],fl[i]);
                if(!vis[v]) vis[v] = 1,q.push(v);
            }
        }
    }
    if(dis[t]!=2e9) return 1;
    return 0;
}
signed main()
{
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    cin>>n>>m>>s>>t;
    for(int i = 1,u,v,w,flow;i<=m;i++)
        cin>>u>>v>>flow>>w,add(u,v,w,flow);
    int ans1 = 0,ans2 = 0;
    while(spfa())
    {
        ans1+=mn[t],ans2+=mn[t]*dis[t];
        int x = t;
        while(x!=s)
        {
            fl[now[x]]-=mn[t],fl[now[x]^1]+=mn[t];
            x = to[now[x]^1];
        }
    }
    cout<<ans1<<' '<<ans2<<'\n';
    return 0;
}

至于最大费用最大流的求法，你可以更改一下 SPFA 或者将费用取反写最小费用最大流都可以。

还是来几道例题吧（可能比较多，读者可以选择性阅读）。

例题一：P2045。

考虑将每个点 $(x,y)$ 拆分为 $in_{x,y},out_{x,y}$，建立超级原点 $S$，汇点为 $out_{n,n}$。连一条 $S\to in_{1,1}$，费用为 $0$，容量为 $k$ 的边，表示最多走 $k$ 次。对于一个点 $(x,y)$，有如下几种边：

一条 $in_{x,y}\to out_{x,y}$，费用为 $a_{x,y}$，容量为 $1$ 的边（只能取一次），表示将 $(x,y)$ 中的数取出来；
一条 $in_{x,y}\to out_{x,y}$，费用为 $0$，容量为 $\infty$ 的边，表示直接跳过 $(x,y)$；
一条 $out_{x,y}\to in_{x+1,y}$ 或者 $out_{x,y}\to in_{x,y+1}$，费用为 $0$，容量为 $\infty$ 的边，表示往下或者往右走。

跑最大费用最大流即可。

例题二：P3358。

首先发现一个开区间对其内部的点都有相同的覆盖次数贡献，所以可以对区间的两个端点离散化。

首先可以想到将数轴上的点用费用为 $0$，容量为 $k$ 的边连成一条链，如何刻画当前点的覆盖次数是现在的首要问题。

设流入当前点的流量为 $f$，那么考虑构造一个网格，使得 $k-f$ 成为这个点的覆盖次数。明显对于线段 $i$，连一条 $l_i\to r_i$，容量为 $1$，费用为其长度的边可以符合条件。

建立超级源点和超级汇点跑最大费用最大流即可。

例题三：CF277E。

发现一个点选父亲和这个点选儿子是互相独立的，所以考虑拆点，$in_x$ 表示这个点去选儿子，$out_x$ 表示这个点的父亲被选好了。

建立超级源点 $S$，$S$ 向每个 $in_x$ 连一条费用为 $0$，容量为 $2$ 的边，表示最多选两个儿子。建立超级汇点 $T$，每个 $out_x$ 向 $T$ 连一条费用为 $0$，容量为 $1$ 的边，表示这个点的父亲选完了，最多一个父亲。

如果两个点 $x,y$ 满足 $x$ 可以成为 $y$ 的父亲，连一条 $in_x\to out_y$ ，容量为 $1$，费用为两点距离的边，这样最终的费用就是此树的权值。

跑最大费用最大流即可，值得注意的是如果最终的最大流不是 $n-1$，就无解，因为除了根节点之外，每个点都得有父亲。

例题四：CF863F。

首先可以暴力预处理出每个点的最终范围 $l_i\sim r_i$，显然如果 $l_i>r_i$ 无解，否则必然有解。

注意到 $x^2=1+3+\cdots+(2x-1)$。将每种权值拆分为两个点 $in_i$ 和 $out_i$，分别连上容量为 $1$，费用为 $1,3,\cdots,2n-1$ 的边，如果有 $k$ 个流量流入了 $in_i$，相当于有 $k$ 个数的值为 $i$，跑最小费用最大流最终的费用刚好是 $k^2$，符合题目所求。

最后的建图就十分显然了，建立超级源点 $S$，$S$ 向每个 $i$ 连容量为 $1$，费用为 $0$ 的边，表示每个 $a_i$ 只能选一个数，每个 $i$ 向 $in_{l_i\sim r_i}$ 连容量为 $1$，费用为 $0$ 的边，表示 $a_i$ 可以选这个数。建立超级汇点 $T$，每个 $out_i$ 向 $T$ 连容量为 $\infty$，费用为 $0$ 的边。

然后跑最小费用最大流即可。

放一道不错的练习题：P4249以及其双倍经验CF1264E。

Part.4 最小割及其应用

定义一张图的割为一种点的划分方式：将图分为 $s,t$ 两个集合，其中 $S\in s,T\in t$。割的权值为 $ \sum\limits_{u\in s,v\in t} c_{u,v}$。最小割就是权值最小的割。

最小割的几个性质：

最小割和最大流是相等的，即最大流最小割定理；
最小割的割边一定是满流边；
若删掉或减小某条满流边的容量后最大流不减小，则该边一定不是最小割中的边；
网络流的任意一条增广路至少经过一条最小割边；
对于某满流边，如果在残留网络中，源点能到达该边一端点，另一端点能到达汇点，则该满流边就是关键割边（即一定是最小割的一个割边）。

例题一：最大权闭合子图。

给出一张有向图 $G=(V,E)$，每个点有一个权值 $w_i$。现在要选出一个点集 $V'$，满足对于任意一条边 $x\to y$，如果 $x\in V'$，则 $y\in V'$。你需要让 $\sum\limits_{x\in V'}w_x$ 最大。

首先考虑最理想的情况，即所有 $w_i>0$ 的点都被选，问题就变成了最小代价（删掉正点权或加入负点权）。所以考虑用最小割求解，这是一种非常常见的套路。

设在一组割中与 $S$ 相连的点就是选，否则就是不选。对于 $w_i>0$ 的点，连边 $S\to i$，容量为 $w_i$，对于 $w_i<0$ 的点，连边 $i\to T$，容量为 $-w_i$。

对于在原图中的一条边 $x\to y$，连一条 $x\to y$，容量为正无穷的边。这样就能保证如果 $x$ 在集合 $s$ 里，$y$ 肯定在集合 $s$ 里，否则这组割的权值就会加上 $\infty$，肯定不是最小的。

跑出来的最大流就是最小的代价，这样答案就能被轻松求出。

例题二：P2057。

考虑用最小割求解，在一组割中，与 $S$ 相连就是投赞成票，否则就是投反对票。

首先如果 $i$ 意愿赞成，就与 $S$ 连一条容量为 $1$ 的边，否则就向 $T$ 连一条容量为 $1$ 的边。这样如果这条边是割边，就会因与自己意愿相反对割贡献 $1$ 的权值。

对于一个朋友关系 $(x,y)$，连两条 $x\to y,y\to x$ 容量为 $1$ 的边，如果两个点不在同一集合内，其中一条边会对割贡献 $1$ 的权值。

跑最小割即可。

练习题：P4313。

Part.5 上下界网络流及其应用

首先什么是上下界网络流，就是每条边除了流出网络的上限 $c_{u,v}$（即容量），新增了一个性质：下界 $b_{u,v}$，要求 $b_{u,v}\le f_{u,v}\le c_{u,v}$。

首先是无源汇上下界可行流。

什么是无源汇，相当于网络中的每个点都满足流量守恒。让你求出满足这些条件的一种流法。

首先先考虑去掉下界的限制，即每条边先流出 $b_{u,v}$ 的流量。但这样明显会不符合流量守恒，考虑建一张图去调整。

设 $ in_u=\sum\limits_{(v,u)\in E} b_{v,u},out_u=\sum\limits_{(u,v)\in E} b_{u,v}$。如果 $in_u>out_u$，说明还需要流出 $in_u-out_u$ 的流量，否则还需要流入 $out_u-in_u$ 的流量。

考虑建图求解，对于 $in_u>out_u$，连一条 $S\to u$，容量为 $in_u-out_u$ 的边；如果 $out_u>in_u$ 连一条 $u\to T$，容量为 $out_u-in_u$ 的边。对于 $(u,v)\in E$，连一条 $u\to v$，容量为 $c_{u,v}-b_{u,v}$。对于这个图跑网络流最大流，如果所有与 $S$ 相连的边都是满流，原图就有可行流（实际流量为图中这条边的流量加上 $b_{u,v}$），否则无解。

加上费用也很简单，用 $\sum\limits_{(u,v)\in E} b_{u,v}\times w_{u,v}$ 加上最小费用最大流即可。

那如何求有源汇上下界可行流/最大流/最小流呢？

第一个直接转化为无源汇上下界可行流，连一条 $T\to S$，下界为 $0$，上界为 $\infty$ 即可。跑出一组可行流后，此时的真实流量是 $T\to S$ 的流量，记为 $f_1$。

那如何求最大流呢？

考虑调整法。还记得求可行流时建的图吗，其实我们只需要拆掉 $T\to S$ 的边，然后再跑一遍 $S\to T$ 的最大流，记为 $f_2$。两者相加就行了。

同样的去求最小流，发现跑 $T\to S$ 的最大流相当于退流，记为 $f_2$，两者相减就行了。

这里放一下求最大流的模板的代码：

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 2e2+5,M = 1e4+N;
int n,m,s,t,ss,tt,a[N],cnt = 1,head[N],to[M<<1],nxt[M<<1],g[M<<1]; 
inline void add(int x,int y,int z)
{
    nxt[++cnt] = head[x];
    head[x] = cnt;
    to[cnt] = y,g[cnt] = z;
    nxt[++cnt] = head[y];
    head[y] = cnt;
    to[cnt] = x,g[cnt] = 0;
}
int dis[N],now[N];
inline bool bfs()
{
    for(int i = 0;i<=n+1;i++) dis[i] = -1;
    queue<int> q;
    q.push(s);
    dis[s] = 0;
    now[s] = head[s];
    while(!q.empty())
    {
        int u = q.front();q.pop();
        for(int i = head[u];i;i = nxt[i])
        {
            int v = to[i];
            if(g[i]>0&&dis[v]==-1)
            {
                q.push(v);
                dis[v] = dis[u]+1,now[v] = head[v];
                if(v==t) return 1;
            }
        }
    }
    return 0;
}
int dfs(int u,int s)
{
    if(u==t) return s;
    int k,res = 0;
    for(int i = now[u];i;i = nxt[i])
    {
        if(!s) break;    
        int v = to[i];
        now[u] = i;
        if(g[i]>0&&dis[v]==dis[u]+1)
        {
            k = dfs(v,min(s,g[i]));
            if(k==0) dis[v] = 2e9;
            g[i]-=k,g[i^1]+=k,res+=k,s-=k;
        } 
    }
    return res;
}
inline int dinic()
{
    int res = 0;
    while(bfs()) res+=dfs(s,2e18);
    return res;
}
signed main()
{
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    cin>>n>>m>>ss>>tt;
    s = 0,t = n+1; 
    for(int i = 1,u,v,c,b;i<=m;i++)
    {
        cin>>u>>v>>b>>c;
        add(u,v,c-b);
        a[u]-=b,a[v]+=b;
    }
    int mx = 0;
    for(int i = 1;i<=n;i++)
        if(a[i]>0) add(s,i,a[i]),mx+=a[i];
        else if(a[i]<0) add(i,t,-a[i]);
    add(tt,ss,1e18);
    if(dinic()<mx) return cout<<"please go home to sleep",0;
    mx = g[cnt];
    g[cnt] = g[cnt-1] = 0;
    s = ss,t = tt;
    cout<<mx+dinic();
    return 0;
}

例题一：P4843。

建立超级源点 $S$，以及超级汇点 $T$。$S$ 向每个 $i$ 建立下界为 $0$，上界为 $\infty$ 的边，每个 $i$ 向 $T$ 连一条下界为 $0$，上界为 $\infty$ 的边。由于原图中的每条边 $(u,v)$ 都得覆盖一次，于是连一条 $u\to v$，下界为 $1$，上界为 $\infty$ 的边。

跑有源汇上下界最小流即可。

例题二：P5192。

对于每天和每个少女飞别建一个点，建超级源点 $S$，以及超级汇点 $T$。每个少女 $x$ 向汇点连下界为 $G_x$，上界为 $\infty$ 的边，源点向第 $x$ 天连一条下界为 $0$，上界为 $D_x$ 的边。第 $x$ 天向第 $y$ 个拍照的少女 $T_{x,y}$ 连一条下界为 $L_{x,y}$，上界为 $R_{x,y}$ 的边。

跑有源汇上下界最大流即可。

Part.6 二分图

一张图是二分图当且仅当这张图可以分为两个不相交的点集 $A,B$，即 $A\cup B=V,A\cap B=\emptyset$，满足不存在 $(u,v)\in E$ 使得 $u\in A,v\in A$ 或者 $u\in B,v\in B$。

一个图是二分图的充分必要条件是这张图里面没有奇环。当然也可以用黑白染色来判断一个图是否是二分图。

二分图的边覆盖/匹配/点覆盖/独立集问题

对于一张图，有如下定义：

边覆盖：$G$ 的一个边集 $E'\subseteq E$ 满足其是 $G$ 的边覆盖，当且仅当对于每个点 $x\in V$，存在另一个点 $y$ 使得 $(x,y)\in E'$，即每个点至少是 $E'$ 中一条边的端点；
匹配：$G$ 的一个边集 $E'\subseteq E$ 满足其是 $G$ 的匹配，当且仅当 $E'$ 中任意两条边不存在共同点；
点覆盖：$G$ 的一个点集 $V'\subseteq V$ 是 $G$ 的点覆盖当且仅当对于图中每条边，其端点至少有一个属于 $V'$；
独立集：$G$ 的一个点集 $V'\subseteq V$ 是 $G$ 的点覆盖当且仅当对于图中每条边，其端点至多有一个属于 $V'$；

事实上，对于任意一张图 $G=(V,E)$，有：

如果 $G$ 存在边覆盖，则最小边覆盖加上最大匹配等于 $|V|$。
证明：首先构造出一个最大匹配 $E'$，记其端点组成的集合大小为 $c$，明显 $c=2|E'|$，现在考虑加边是其变为最小边覆盖，而每加一条边 $c$ 会加一，最后我们需要将 $c$ 变为 $|V|$，所以加边个数为 $|V|-2|E'|$，最小边覆盖为 $|V|-2|E'|+|E'|=|V|-|E'|$，得证。
$G$ 的最大独立集加上最小点覆盖大小刚好为 $|V|$。
证明：对于 $G$ 的最大独立集 $V'$，显然每条边最多只有一个端点属于 $V'$。令 $V''=V-V'$，则每条边至少一个端点属于 $V''$，这刚好与点覆盖的定义相同，即 $V''$ 就是这张图的最小点覆盖。

二分图最大匹配模板。

建立超级源点 $S$ 以及超级汇点 $T$，将原图中的每个点 $u$ 拆分为两个点 $in_u,out_u$，$S$ 向每个 $in_u$ 连容量为 $1$ 的边（$u$ 最多匹配一个点），每个 $out_u$ 向 $T$ 连容量为 $1$ 的边（$u$ 最多被一个点匹配）。对于每个可能的匹配 $(u,v)$，连 $in_u\to out_v$ 且容量为 $1$ 的边。这样建出来的图跑最大流即为答案。

二分图有一个性质就是最大匹配等于最小点覆盖，虽然笔者不会证明，但是这意味着求出了二分图最大匹配就相当于求出了另外三个的值。

接下来就是例题。

例题一：P4251。

这种每行选一个使得没有重复的列的题都有一个套路：将行和列连边，然后跑二分图最大匹配。

首先想到二分答案，我们需要判断答案是否小于等于 $x$。将所有小于等于 $x$ 的数置为可以选的，容易用二分图最大匹配求出当前能最多选几个数，最后判断是否大于等于 $n-k+1$ 个数即可。

例题二：P2764。

首先当每个点自成一条路径的时候，当前的路径条数为 $n$，可以考虑一条边 $(x,y)\in E$，满足覆盖 $x$ 的链没有后继，覆盖 $y$ 的链没有前驱。将这两条链合并起来，自然会使路径数减一。

将每个点拆分为两个点 $a_x,b_x$，$a_x$ 被选相当于 $x$ 有了后继，$b_x$ 被选相当于 $x$ 有了前驱，发现每条边 $(x,y)$ 相当于将 $a_x$ 和 $b_y$ 匹配起来，这就是典型的二分图最大匹配了。

现在的问题在于如何输出方案。不难发现在图中流往哪个边流相当于这条边两个端点在同一条链里面，这样记录方案也非常简单了。

练习题：CF1592F2。

Hall 定理

注：此知识点几乎和网络流没有关系，仅为对二分图的补充，读者可以选择性阅读。

Hall 定理：对于一张二分图 $G=(V_1,V_2,E)$，定义函数 $f(V)(V\in V_1)$ 为与点集 $V$ 中相邻点的并集，那么二分图有完美匹配的充要条件为 $\forall V\subseteq V_1,|f(V)|\ge |V|$。笔者暂时不会证明。

练习题：CF338E。

posted @ 2025-02-21 14:17 pyy1 阅读(89) 评论(0) 收藏举报

刷新页面返回顶部

PizzaYY 的小窝