counter汇总：环形计数器、扭环计数器、LSFR计数器

计数器

环型计数器

环型计数器就是最简单的移位寄存器，对应N位环型计数器有N个状态。

反馈逻辑函数为：

\[D_0 = Q_{n-1} \]

verilog code

module round_counter
(
	input clk,
	input rst_n,
	output reg [3:0] q
);

	always @(posedge clk or negedge rst_n)begin
		if(!rst_n)begin
			q <= 4'b1000;
		end
		else
      q <= {q[0], q[3:1]};
	end
endmodule

扭环计数器

环形计数器不同的是将最低位取反后移位到最高位，其计数长度为N = 2n，经过n个时钟后，计数器状态与初始状态刚好相反，然后再经过n个时钟返回初始状态。

\[D_0 = \overline{Q_{n-1}} \]

module round_counter
(
	input clk,
	input rst_n,
	output reg [3:0] q
);

	always @(posedge clk or negedge rst_n)begin
		if(!rst_n)begin
			q <= 4'b0000;
		end
		else
			q <= {~q[0], q[3:1]};
	end
endmodule

线性反馈移位寄存器

线性反馈移位寄存器(LFSR),它是由n个D触发器和若干个异或门组成的。LFSR可以产生的最长的随机序列是\(2^n-1\)，对应抽头不同，产生的随机序列长度也不同。

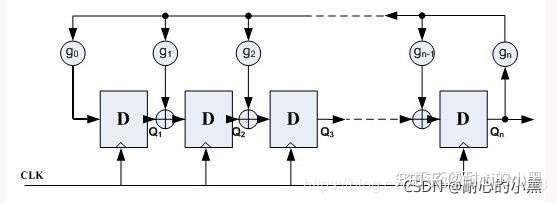
有两种实现方式，一种IE型，异或门内接（伽罗瓦）的线性反馈移位寄存器；

另一种是异或门外接（斐波那契）的线性反馈移位寄存器，简称EE型LFSR：

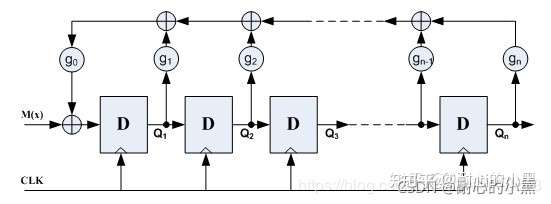
其中，\(g_n\)为反馈系数，取值只能为0或1，取为0时表明不存在该反馈之路，取为1时表明存在该反馈之路，n个D触发器最多可以提供\(2^n-1\)个状态(不包括全0的状态)。为了保证这些状态没有重复，\(g_n\)的选择必须满足一定的条件。

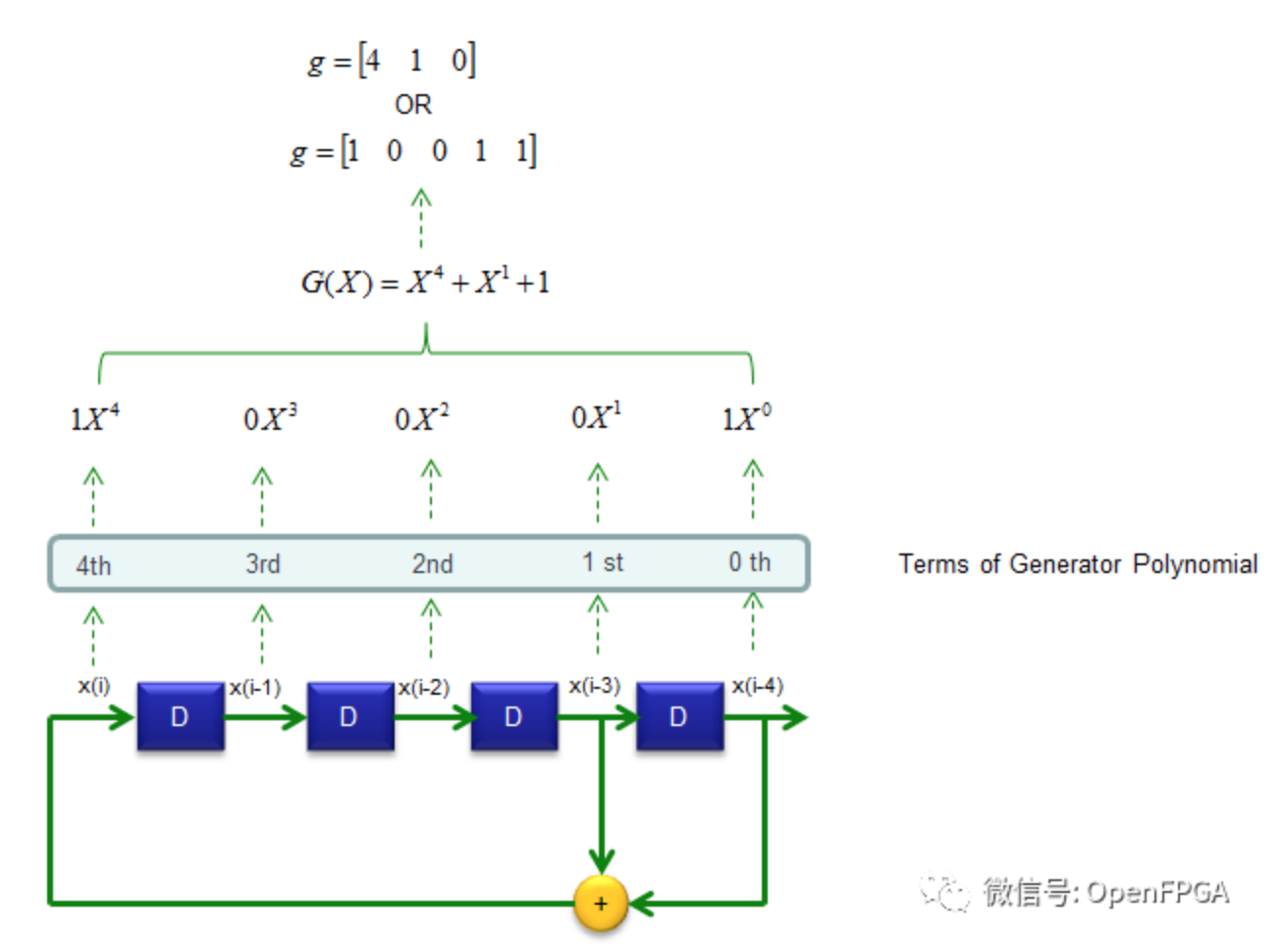
多项式表示，如果抽头为在第16，14，13，11个比特，则相应的特征多项式为：

如图，有反馈路径的\(g_n\)为1，反之为0

module RanGen(
    input               rst_n,    /*rst_n is necessary to prevet locking up*/
    input               clk,      /*clock signal*/
    input               load,     /*load seed to rand_num,active high */
    input      [7:0]    seed,     
    output reg [7:0]    rand_num  /*random number output*/
);


always@(posedge clk or negedge rst_n)
begin
    if(!rst_n)
        rand_num    <=8'b0;
    else if(load)
        rand_num <=seed;    /*load the initial value when load is active*/
    else
        begin
            rand_num[0] <= rand_num[7];
            rand_num[1] <= rand_num[0];
            rand_num[2] <= rand_num[1];
            rand_num[3] <= rand_num[2];
            rand_num[4] <= rand_num[3]^rand_num[7];
            rand_num[5] <= rand_num[4]^rand_num[7];
            rand_num[6] <= rand_num[5]^rand_num[7];
            rand_num[7] <= rand_num[6];
        end
            
end
endmodule