第三部分—机器学习
本章内容介绍第三部分,人工智能的核心:机器学习。
常用算法
决策树(DT)
决策树类似一种树形的数据结构,在每个节点回答一个问题并根据答案决定后续的走向。如果只是基于这样的树型结构决策,那么很容易使用if-else语句完成,因此这里智能体现在自动的从样本点构建决策树,构建的方法如下:类似深度优先搜索,每次选择一个特征构建新的子树。这里每次选择的特征不是随机选取的,因为随机选取的决策效率往往不高,我们需要选择能够尽量使上一阶段中得到的样本不同类别分开,而分开与否的度量标准就是信息熵。
信息熵:对于概率事件\(<P_1, P_2, P_3, \ldots, P_n>\),\(H(<P_1, P_2, P_3, \ldots, P_n>) = \sum^n_{i=1}Plog_2^{\frac{1}{P}}\),\(log_2^{\frac{1}{P}}\)为编码位的下限。他可以用来表示需要传输的最小信息量。
例如:需要讨论苹果的特征之间的关系,分为两个特征:颜色(红,半红,不红)和甜度(甜,不甜)。对于下面的这个样本,有如下的分析:
红色苹果中,有3个甜苹果,1个不甜苹果;半红苹果中,有2个甜苹果,2个不甜苹果;不红苹果中,有2个甜苹果,3个不甜苹果。按照颜色分组前,信息熵为\(-\frac{7}{13}log\frac{7}{13}-\frac{6}{13}log\frac{6}{13}\),在按照颜色分组后,信息熵为\(-\frac{4}{13}\times\frac{3}{4}log\frac{3}{4}-\frac{4}{13}\times\frac{1}{4}log\frac{1}{4}-\frac{4}{13}\times\frac{2}{4}log\frac{2}{4}-\frac{4}{13}\times\frac{2}{4}log\frac{2}{4}-\frac{5}{13}\times\frac{2}{5}log\frac{2}{5}-\frac{5}{13}\times\frac{3}{5}log\frac{3}{5}\),信息熵下降了0.045,这里信息熵的下降被称为信息增益,信息增益越大,这个特征的区别作用越明显。
除了信息熵之外,还有另一种有名的判别方法,称为基尼指数(Gini Index),他的基本公式是\(Gini(D) = 1 - \sum (p_i²)\),二者并没有本质上的区别,计算的结果基本呈正相关,只是不同的计算机科学家在研究同一个问题时提出的不同方案。
随机森林
随机森林是一种由多个决策树构成的集成学习方法。其训练过程如下:
- 样本随机(Boostrap)采样
从训练集中中以有放回抽样的方式随机抽取N个样本,生成一个自助样本集。重复此过程M次,得到M个训练子集
- 特征随机
在每棵决策树的每个节点进行分裂时,从全部特征中随机选取m个特征(通常\(m \leq \sqrt{总特征数}\)),然后从这m个特征中选择最佳分裂点。
- 完全生长
每棵决策树不进行剪枝,完全生长(直到叶子节点纯度达到最大或样本数过少)。
随机森林既可以完成分类任务,也可以完成回归任务。如果是分类任务,那么将使用以下公式$$\hat{y}=mode\{h_1(x),h_2(x),\ldots,h_M(x)\}$$即多数投票结果。如果是回归任务,最终预测公式为$$\frac{1}{M}\sum^M_{m=1}h_m(x)$$即所有树的平均。
例如,以相亲为例,对于以下的样本
| 编号 | 年龄 | 颜值 | 收入(万/年) | 爱好匹配度 | 距离(km) | 是否接受 |
|---|---|---|---|---|---|---|
| 1 | 25 | 高 | 10 | 高 | 5 | 是 |
| 2 | 30 | 中 | 20 | 中 | 20 | 是 |
| 3 | 28 | 低 | 8 | 高 | 15 | 否 |
| 4 | 35 | 高 | 25 | 低 | 50 | 否 |
| 5 | 22 | 中 | 6 | 高 | 10 | 是 |
| 6 | 40 | 低 | 15 | 中 | 30 | 否 |
| 7 | 26 | 高 | 12 | 高 | 8 | 是 |
| 8 | 33 | 中 | 18 | 低 | 25 | 否 |
| 9 | 29 | 高 | 22 | 中 | 12 | 是 |
| 10 | 31 | 低 | 9 | 高 | 18 | 否 |
第一步 构建决策树(以其中一棵为例)
-
行采样,从10个样本中有放回的抽取10次,假设抽到[1, 2, 2, 5, 7, 7, 9, 10, 3, 1]
-
对该树进行训练,随机挑选3个特征(总共5个特征)进行学习
根节点分裂:
- 随机选择的特征子集:
[年龄, 颜值, 距离] - 最佳分裂点:
年龄 > 28
以此类推,最终得到五棵树的所有情况
| 树编号 | 行采样示例 | 特征随机性 | 主要分裂规则 |
|---|---|---|---|
| 树1 | [1,2,2,5,7,7,9,10,3,1] | m=3 | 年龄>28 → 收入>20 |
| 树2 | [3,4,5,6,8,8,9,10,2,4] | m=3 | 颜值=高 → 距离<20 |
| 树3 | [1,1,3,5,6,7,9,9,10,10] | m=3 | 爱好匹配度=高 → 年龄<30 |
| 树4 | [2,3,4,5,7,8,9,9,10,10] | m=3 | 收入>15 → 距离<25 |
| 树5 | [1,2,3,4,5,6,7,8,9,10] | m=3 | 年龄<35 → 爱好匹配度=中 |
第二步 根据森林预测新的样本,只要按照上述分类任务的少数服从多数原则即可。
k近邻算法(KNN)
k近邻算法,顾名思义就是取待判别点周围的k个点进行统计,哪一类的点更多就归为哪一类。虽然这个方法看起来十分简单轻巧,但是根据理论分析,当样本数量趋近无穷大时,k近邻算法得到的是最优决策。
在使用k近邻算法时,为了减少搜索临近k个点的时间复杂度,需要引入一种新的数据结构:k-d树。
k-d树:k-d树的构建是一个不断求解中位数的过程:对于样本点中每一个多维向量,按照维度循环遍历并求中位数,然后以数的大小为判断依据递归的求解左右子树。例如,要将数据集定义为\(\mathcal{D} = \big\{ (2,3)^T,\ (5,4)^T,\ (9,6)^T,\ (4,7)^T,\ (8,1)^T,\ (7,2)^T \big\}\)的样本转化为k-d树,要经历以下几步:
- 找到x轴的全局中位数,发现有两个数都符合要求(5,7),那么我们可以随机选取一个作为中位数,比如说我们选取了7作为中位数,那么应该以7为横坐标进行左右空间的划分,如下图所示。
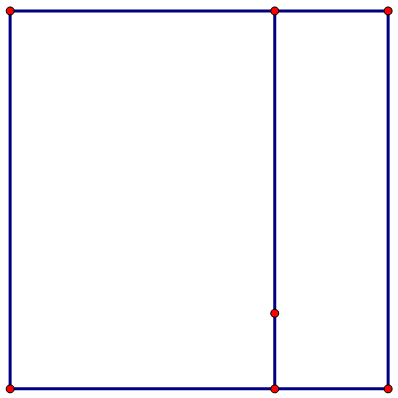
- 然后再以7为中轴的空间的左右两边,我们分别再找到以横轴为划分的两条中位线,分别为4和6,划分之后如下图所示。
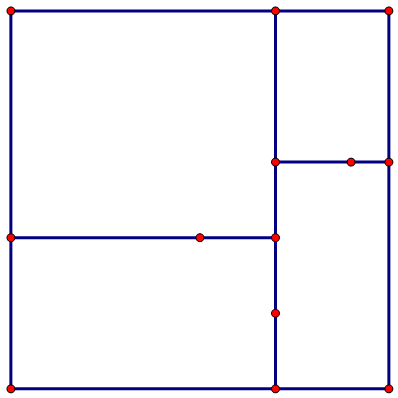
- 最后,我们构建第三层的元素,这时划分的依据又回到了横轴,我们需要填满剩余所有的节点,如下图所示。
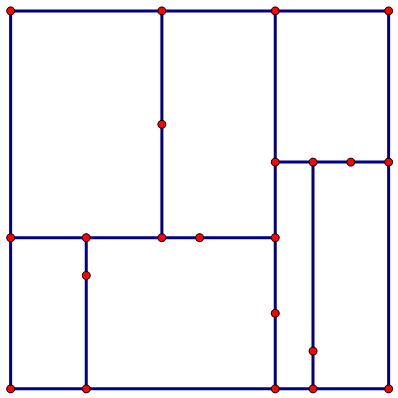
最终构建的的树如下图所示。
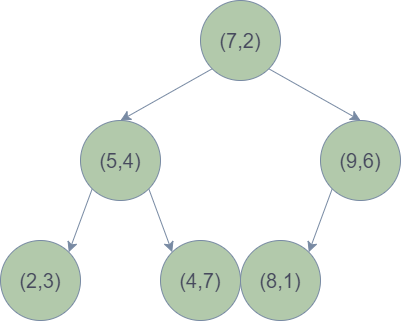
有了k-d树,搜索最近邻就变得非常方便。
1)搜索目标点。若当前层对应的维度值比目标点大,则递归求解左子树,否则递归求解右子树,并将当前节点压栈,直到找到叶子结点,并求其与目标节点的距离记为minDist;
2)回溯路径,若当前节点是叶子结点,那么只需要判断是否需要修改minDist即可,若不是叶子结点,则需要经过三步:
\(a)\) 判断是否需要修改minDist,
\(b)\) 计算目标与当前节点所划分的超平面的距离(所谓超平面,就是以当前节点的某一个维度为轴画出的平面,在二维坐标系下就是上面示意图中点所在的线段)
\(c)\) 若距离大于minDist,则不做任何操作,否则从1)开始对当前节点的另一棵子树求解,不断循环直到2)中栈空。
朴素贝叶斯算法
贝叶斯分类算法是一系列分类算法的统称,其中最简单的就是朴素贝叶斯算法。要了解贝叶斯算法,就要了解贝叶斯概率中的三个重要概念
- 先验概率:事件发生前的预判概率,可以是基于历史数据的统计,背景常识或人的主观观点
例如,按照往年数据,一个西瓜是好瓜的概率是60%,那么这个\(P(好瓜)\)就是先验概率
- 后验概率:事件发生后求的反向条件概率
例如,纹理清晰的瓜是好瓜的概率为75%,如果把纹理清晰当做结果,那么这个\(P(好瓜|纹理清晰)\)就是后验概率
- 条件概率:一个事件发生的情况下另一个事件发生的概率
在贝叶斯算法中,常常需要使用贝叶斯定理,即全概率公式,通过条件概率(似然概率)\(P(B|A)\)求解后验概率\(P(A|B)\)。
朴素贝叶斯算法中,所谓的朴素就是假设特征之间条件独立,这样就可以得到\(P(x_1,x_2,\ldots,x_n | y) = P(x_1 | y)P(x_2 | y) \ldots P(x_n | y)\)。虽然这种条件在大部分情况下都是不成立的,但是这个算法在实验上却有着非常好的准确度,因此这个条件就理所当然的被沿用了下来。
为了得到分类结果,就需要在不同情况下计算相应的后验概率。假设\(x_1,x_2,\ldots,x_n\)是一组结果,为了推出y的类别,可以使用贝叶斯公式,即\(P(y_k|x_1,x_2,\ldots,x_n) = P(y = y_k)P(x_1|y = y_k) \ldots P(x_n|y = y_k)\),然后遍历计算所有的\(y_k\)并找到最大的后验概率,就是y的分类结果。
例如,对于有特征1 \(color=\{1,2,3,4\}\)和特征2 \(weight=\{0,1,2,3,4\}\)的以下样本
| color | weight | sweet? |
|---|---|---|
| 3 | 4 | yes |
| 2 | 3 | yes |
| 0 | 3 | no |
| 3 | 2 | no |
| 1 | 4 | no |
为了计算\(color=3,weight=3\)的样品西瓜甜不甜,我们需要分别计算甜和不甜的概率
\(p_1 = P(sweet=yes|color=3,weight=3) = P(color=3|sweet=yes)P(weight=3|sweet=yes)P(sweet=yes)\)
\(p_2 = P(sweet=no|color=3,weight=3) = P(color=3|sweet=no)P(weight=3|sweet=no)P(sweet=no)\)
然后比较\(p_1\)和\(p_2\)即可。
然而,这里仍然存在一个问题,即当出现根本不存在的样本时,概率会因为这一个或几个条件而永远为0,影响有效数据对结果的贡献。例如对于\(f(y|color=0,weight=1)\),\(p_1=p_2=0\),此时我们需要进行拉普拉斯修正。
拉普拉斯修正:每个条件都添加一个完整的样本到样本集中
例如,对于上面的反例,可以在求\(P(color=0|sweet=yes)\)时添加\(\{color=0~3,weight=1,sweet=yes\}\),这样其概率变为\(\frac{0+1}{2+4}\),在求\(P(weight=3|sweet=yes)\)时,添加\(\{color=0,weight=0~4,sweet=yes\}\),这样其概率变为\(\frac{0+1}{2+5}\),在求\(P(sweet=yes)\)时添加\(\{color=0,weight=1,y=yes,no\}\),这样其概率变为\(\frac{2+1}{2+5}\)。这样最终的概率就可以进行区分。
机器学习中的误差与优化
在机器学习中,我们希望得到泛化误差比较小的模型,即表现好的模型,但是我们只能看到训练数据集的误差,即样本误差。
误差计算
对于分类问题和回归问题,误差计算有所区别,因为分类问题(计算物体所属的类别)往往离散的,而回归问题(计算物体特征的值)往往是连续的。
分类问题
\(\epsilon=\frac{1}{m}\sum I(h(x_i) \neq y_i)\)
\(E=\sum p_i I(h(x_i) \neq f(x_i))\)
回归问题
\(\epsilon=\frac{1}{m}\int (h(x_i) - y_i)^2\)
\(E=\int p_i (h(x_i) - f(x_i))^2\)
这里使用平方一个重要的原因是当误差 \(\epsilon\) 服从独立同分布的正态分布 \(\epsilon \sim N(0, \sigma^2)\)时,最小化平方误差等价于最大化似然函数。同时,在经典线性回归假设下最小二乘估计(使用平方误差)是最佳线性无偏估计(即估计的方差最小)。
似然函数:前面提到的f,用于表示在给定观测到数据的前提下,选择最可能产生这些观测结果的模型参数
方差 (variance) 与偏差 (bias)
variance和bias是机器学习中判断模型好坏的重要指标,在一定程度上可以反应模型的拟合程度。下面我们将从期望的角度推导Bias-Variance Dilemma这个著名的两难问题。注:D表示某一数据集
这里推导出的第一项是\(variance\),表示的是模型预测与期望预测情况的偏差,第二项是\(bias^2\),表示期望与真实情况的偏差,第三项加粗部分可以做变换$$E_D[2(h(\vec{x})-E_D[h(\vec{x})])(E_D[h(\vec{x})]-f(\vec{x}))]$$
因此这一项可以直接消去。
| 操作 | \(variance\) | \(bias\) |
|---|---|---|
| 减少假设空间 | 下降 | 上升 |
| 增大假设空间 | 上升 | 下降 |
假设空间(hypothesis space):模型族的搜索范围,模型训练时将会从中选择与数据集最吻合的函数或节点选择。
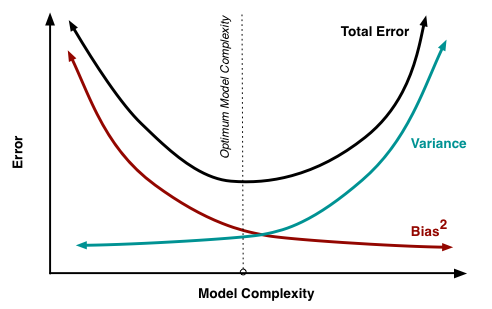
可以发现,模型总的效果的期望值同时受两方面影响,然而两个因素呈负相关。因此我们几乎无法同时提高variance和bias。
最终,由于这两个因素的存在,大多数模型的训练效果会呈现如下图的曲线。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号