OpenCV3入门(十二)角点检测
1、角点介绍
角点检测(Corner Detection)是计算机视觉系统中用来获得图像特征的一种方法,广泛应用于运动检测、图像匹配、视频跟踪、三维建模和目标识别等领域中,也称为特征点检测。在图像中角点是一个重要的局部特征,它决定了图像中关键区域的形状,体现了图像中重要的特征信息。目前,角点检测方法主要有2大类:
1)基于图像边缘轮廓特征的方法。
2)基于图像灰度信息的方法。此方法主要通过计算曲率及梯度进行角点检测,通过计算边缘的曲率来判断角点的存在性。典型代表有Harris算法、Susan算法、Moravec算法等。
角点通常被定义为两条边的交点,更严格的说,角点的局部邻域应该具有两个不同区域的不同方向的边界。而实际应用中,大多数所谓的角点检测方法检测的是拥有特定特征的图像点,而不仅仅是“角点”。这些特征点在图像中有具体的坐标,并具有某些数学特征,如局部最大或最小灰度、某些梯度特征等。现有的角点检测算法并不是都十分的健壮。很多方法都要求有大量的训练集和冗余数据来防止或减少错误特征的出现。另外,角点检测方法的一个很重要的评价标准是其对多幅图像中相同或相似特征的检测能力,并且能够应对光照变化、图像旋转等图像变化。
2、Harris算法介绍
Harris 是 Harris 和 Stephens 在 1988 年提出,专门针对 Moravec 算子的改进版。Harris 算子,又称 Plessey算子,它基于与 Moravec 相同的角点定义,即定义在各个方向上灰度值变化的点。
角点可以如下图形象的定义,如果在各个方向上移动这个小窗口,窗口内的灰度发生了较大的变化,那么说明窗口内存在角点;如果在各个方向移动,灰度几乎不变,说明是平坦区域;如果只沿着某一个方向移动,灰度几乎不变,说明是直线(边缘)。
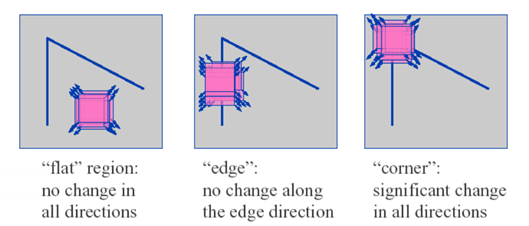
设图像窗口平移[u,v] ,产生的灰度变化为E[u,v] ,则:

上式中,窗口函数是一个矩形窗口或高斯窗口,它给在其中的像素加权。
我们必须使边角检测的函数最大化,这意味着,我们必须最大限度地利用第二个参数。
根据角点的定义,平坦区域,像素变化小,那么上式后半部分基本接近为0;在边缘区域,会在沿着边缘方向上差值为一个稳定值;只有在角点处,无论向那个方向移动,都会发生变化。
根据泰勒级数展开:

那么f(x+u, y+v)可以简化为:
f(x+u, y+v) ≈ f(x,y) + ufx(x,y) + vfy(x,y)
Harris算式的可以写成矩阵模式。
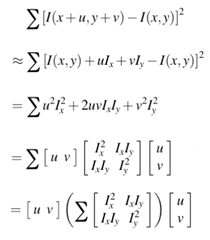
Harris算式可以近似得到下面的表达:
 其中M为:
其中M为:
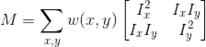
其中,表示 Ix 方向的梯度,表示Iy 方向的梯度,为高斯函数。矩阵的特征值是自相关函数的一阶曲率。特征值的大小与特征点的性质息息相关。即当两个特征值都比较小时,则此点可能位于平坦区,不为角点或边界点; 当两个特征值一个较大、而另一个却相对较小时,则此点位于边界上,属于边界点; 当两个特征值均相对较大时,则此点沿任意方向的曲率都较大,为需要提取的角点。

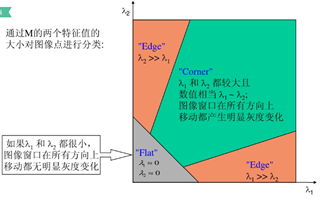
M为梯度的协方差矩阵,在实际应用中为了能够应用更好的编程,定义了角点响应函数R,通过判定R大小来判断像素是否为角点。R取决于M的特征值,对于角点|R|很大,平坦的区域|R|很小,边缘的R为负值。Harris角点检测算法就是对角点响应函数R进行阈值处理:R > threshold,即提取R的局部极大值。

其中,det(M) = λ1* λ1, trace(M) =λ1+ λ1 。k是经验参数,一般取值为0.04~0.06。
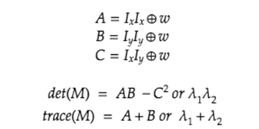
当R为大数值正数的时候,表示为角点。如下图所示:
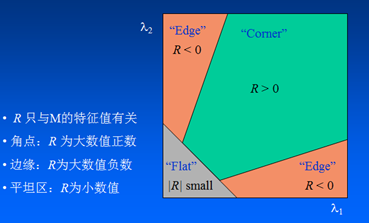
3、Harris实验
OpenCV函数原型:
C++:void cornerHarris( InputArray src, //输入8bit单通道灰度Mat矩阵 OutputArray dst, //保存角点检测结果,32位单通道,大小与src相同 int blockSize, //滑块窗口的尺寸、邻域的大小 int ksize, //Sobel边缘检测滤波器大小 double k, //Harris中间参数,经验值0.04~0.06 int borderType=BORDER_DEFAULT //插值类型 );
测试实例:
int threshod_val = 30; int max_threshod_val = 150; Mat src_img; void call_back(int, void*) { Mat normImage, scaledImage; Mat Img_scr1 = src_img.clone(); Mat Img_dst = Mat::zeros(src_img.size(), CV_32FC1); cornerHarris(src_img, Img_dst, 2, 3, 0.04, BORDER_DEFAULT); //进行角点检测 normalize(Img_dst, normImage, 0, 255, NORM_MINMAX, CV_32FC1, Mat()); // 归一化 convertScaleAbs(normImage, scaledImage);//将归一化后的图线性变换成8位无符号整型 for (int i = 0; i < normImage.rows; i++) { for (int j = 0; j < normImage.cols; j++) { if ((int)normImage.at<float>(i, j) > threshod_val + 100) { circle(Img_scr1, Point(j, i), 3, Scalar(0, 0, 255), 2, 8, 0); circle(scaledImage, Point(j, i), 3, Scalar(0, 0, 255), 2, 8, 0); } } } imshow("corner", Img_scr1); imshow("scaledImage", scaledImage); } int main() { src_img = imread("D:\\WORK\\5.OpenCV\\LeanOpenCV\\pic_src\\checkerboard.png"); imshow("原图", src_img); cvtColor(src_img, src_img, COLOR_BGR2GRAY); namedWindow("corner"); createTrackbar("thresh", "corner", &threshod_val, max_threshod_val, call_back); call_back(threshod_val, 0); waitKey(0); }
输出结果如下图:
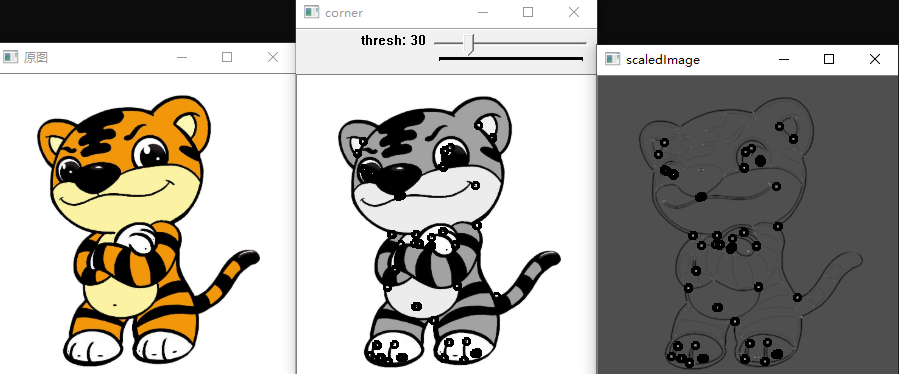
测试2:
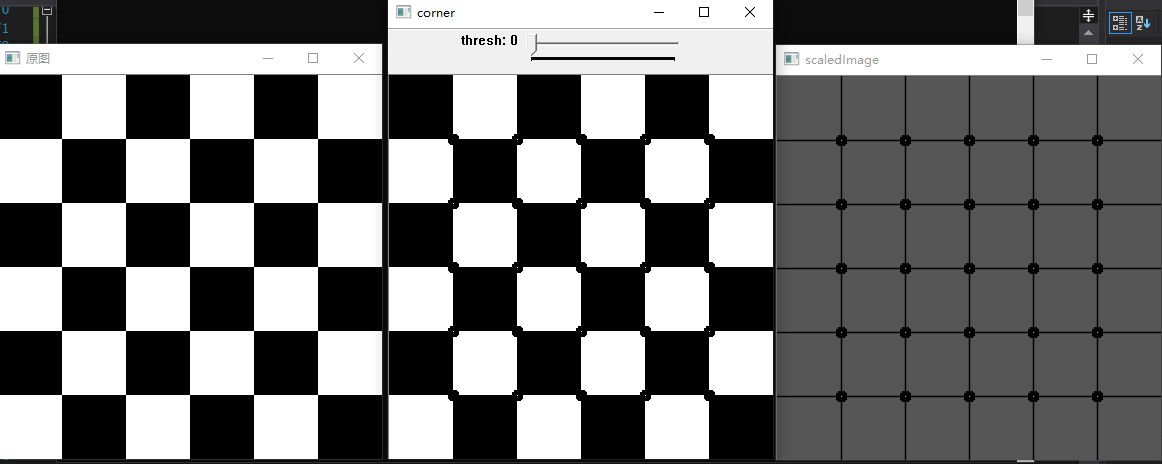
4、参考文献
1、A COMBINED CORNER AND EDGE DETECTOR,Chris Harris,Mike Stephens,1988
http://www.bmva.org/bmvc/1988/avc-88-023.pdf
2、Harris Corner Detection
3、Harris 角点检测子
4、【OpenCV入门教程之十六】OpenCV角点检测之Harris角点检测
https://blog.csdn.net/poem_qianmo/article/details/29356187
5、(四)OpenCV中的特征检测之Harris Corner检测
https://blog.csdn.net/u014403318/article/details/80562785
6、OpenCV学习笔记(八)——Harris角度特征从原理到实现详解
https://blog.csdn.net/weixin_41695564/article/details/79962401
7、《OpenCV3 编程入门》,电子工业出版社,毛星雨著
8、《学习OpenCV》,清华大学出版社,Gary Bradski, Adrian kaehler著
技术博客,转载请注明。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号