【小白学算法】8.二叉树的遍历，前序、中序和后序

二叉树的遍历，同样也是为了访问到树中的每个结点(仅一次)。
不过，由于树的结构与之前的线性存储不同，从根结点开始，二叉树可以有多种的访问次序的选择。
按照我们通常的从左到右的习惯，常见的遍历次序有3种：前序、中序、后续。

一、什么是前序、中序、后序

为了方便说明，暂且我们把访问结点，就当做是打印输出这个结点信息。那么如何区分前中后，也正是根据
输出的先后顺序来定的。

• 前序遍历：先输出父节点，再遍历左子树，然后遍历右子树
• 中序遍历：先遍历左子树，再输出父节点，然后遍历右子树
• 后续遍历：先遍历左子树，再遍历右子树，最后输出父节点

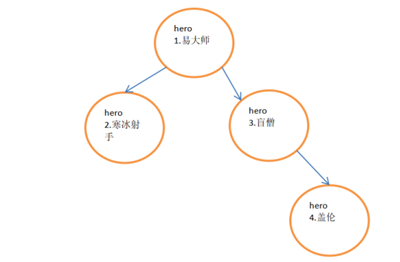
如图所示的二叉树，它的前中后输出顺序分别就是：
1 前序：1易大师、2寒冰射手、3盲僧、4盖伦
2 中序：2寒冰射手、1易大师、3盲僧、4盖伦
3 后序：2寒冰射手、4盖伦、3盲僧、1易大师

二、代码实现前、中、后序遍历

实现思路很简单：

1. 创建英雄结点，在这里编写遍历方法
2. 创建二叉树，调用遍历方法
3. main方法进行测试

package tree;

public class BinaryTreeDemo {
    public static void main(String[] args) {
        // 测试二叉树遍历
        BinaryTree binaryTree = new BinaryTree();
        // 创建结点
        HeroNode hero1 = new HeroNode(1, "易大师");
        HeroNode hero2 = new HeroNode(2, "寒冰射手");
        HeroNode hero3 = new HeroNode(3, "盲僧");
        HeroNode hero4 = new HeroNode(4, "盖伦");

        // 暂时手动创建图示里的结点关系（后面使用递归创建）
        hero1.setLeft(hero2);
        hero1.setRight(hero3);
        hero3.setRight(hero4);
        binaryTree.setRoot(hero1);  // 作为根结点

        //测试前序遍历
        System.out.println("前序遍历测试---------");
        binaryTree.preOrder();

        //测试中序遍历
        System.out.println("中序遍历测试---------");
        binaryTree.infixOrder();

        //测试后序遍历
        System.out.println("后序遍历测试---------");
        binaryTree.postOrder();
    }
}

// 2.创建二叉树
class BinaryTree {
    private HeroNode root;  // 根结点

    public void setRoot(HeroNode root) {
        this.root = root;
    }

    // 前序遍历
    public void preOrder() {
        if (this.root != null) {
            this.root.preOrder();
        } else {
            System.out.println("二叉树为空，无法遍历");
        }
    }
    // 中序遍历
    public void infixOrder() {
        if (this.root != null) {
            this.root.infixOrder();
        } else {
            System.out.println("二叉树为空，无法遍历");
        }
    }
    // 后序遍历
    public void postOrder() {
        if (this.root != null) {
            this.root.postOrder();
        } else {
            System.out.println("二叉树为空，无法遍历");
        }
    }
}

// 1.创建结点
class HeroNode {
    private int No;
    private String name;
    private HeroNode left;
    private HeroNode right;

    public int getNo() {
        return No;
    }

    public void setNo(int no) {
        No = no;
    }

    public String getName() {
        return name;
    }

    public void setName(String name) {
        this.name = name;
    }

    public HeroNode getLeft() {
        return left;
    }

    public void setLeft(HeroNode left) {
        this.left = left;
    }

    public HeroNode getRight() {
        return right;
    }

    public void setRight(HeroNode right) {
        this.right = right;
    }

    public HeroNode(int no, String name) {
        this.No = no;
        this.name = name;
    }

    @Override
    public String toString() {
        return "HeroNode{" +
                "No=" + No +
                ", name='" + name + '\'' +
                '}';
    }

    // 遍历方法
    // 前序
    public void preOrder() {
        System.out.println(this);  // 先输出父节点
        // 左子树递归前序遍历
        if(this.left != null) {
            this.left.preOrder();
        }
        // 右子树递归前序遍历
        if(this.right != null) {
            this.right.preOrder();
        }
    }
    // 中序
    public void infixOrder() {
        // 左子树递归 中序遍历
        if (this.left != null) {
            this.left.infixOrder();
        }
        // 输出父结点
        System.out.println(this);
        // 右子树递归 中序遍历
        if (this.right != null) {
            this.right.infixOrder();
        }
    }
    // 后序
    public void postOrder() {
        // 左子树递归 后序遍历
        if (this.left != null) {
            this.left.postOrder();
        }
        // 右子树递归 后序遍历
        if (this.right != null) {
            this.right.postOrder();
        }
        // 输出父结点
        System.out.println(this);
    }

}

运行测试

前序遍历测试---------
HeroNode{No=1, name='易大师'}
HeroNode{No=2, name='寒冰射手'}
HeroNode{No=3, name='盲僧'}
HeroNode{No=4, name='盖伦'}
中序遍历测试---------
HeroNode{No=2, name='寒冰射手'}
HeroNode{No=1, name='易大师'}
HeroNode{No=3, name='盲僧'}
HeroNode{No=4, name='盖伦'}
后序遍历测试---------
HeroNode{No=2, name='寒冰射手'}
HeroNode{No=4, name='盖伦'}
HeroNode{No=3, name='盲僧'}
HeroNode{No=1, name='易大师'}

Process finished with exit code 0

遍历顺序与上面预测的相符合。
如果有小伙伴对于递归比较陌生的，可以移步到这，【python】递归听了N次也没印象，读完这篇你就懂了。

本章我们知道了遍历二叉树，那如果我要查找二叉树中某一个结点，前中后序这3种的查找思路又是怎样呢？下面继续。