K近邻法(KNN)原理小结
K近邻法(k-nearest neighbors,KNN)是一种很基本的机器学习方法了,在我们平常的生活中也会不自主的应用。比如,我们判断一个人的人品,只需要观察他来往最密切的几个人的人品好坏就可以得出了。这里就运用了KNN的思想。KNN方法既可以做分类,也可以做回归,这点和决策树算法相同。
KNN做回归和分类的主要区别在于最后做预测时候的决策方式不同。KNN做分类预测时,一般是选择多数表决法,即训练集里和预测的样本特征最近的K个样本,预测为里面有最多类别数的类别。而KNN做回归时,一般是选择平均法,即最近的K个样本的样本输出的平均值作为回归预测值。由于两者区别不大,虽然本文主要是讲解KNN的分类方法,但思想对KNN的回归方法也适用。由于scikit-learn里只使用了蛮力实现(brute-force),KD树实现(KDTree)和球树(BallTree)实现,本文只讨论这几种算法的实现原理。其余的实现方法比如BBF树,MVP树等,在这里不做讨论。
1. KNN算法三要素
KNN算法我们主要要考虑三个重要的要素,对于固定的训练集,只要这三点确定了,算法的预测方式也就决定了。这三个最终的要素是k值的选取,距离度量的方式和分类决策规则。
对于分类决策规则,一般都是使用前面提到的多数表决法。所以我们重点是关注与k值的选择和距离的度量方式。
对于k值的选择,没有一个固定的经验,一般根据样本的分布,选择一个较小的值,可以通过交叉验证选择一个合适的k值。
选择较小的k值,就相当于用较小的领域中的训练实例进行预测,训练误差会减小,只有与输入实例较近或相似的训练实例才会对预测结果起作用,与此同时带来的问题是泛化误差会增大,换句话说,K值的减小就意味着整体模型变得复杂,容易发生过拟合;
选择较大的k值,就相当于用较大领域中的训练实例进行预测,其优点是可以减少泛化误差,但缺点是训练误差会增大。这时候,与输入实例较远(不相似的)训练实例也会对预测器作用,使预测发生错误,且K值的增大就意味着整体的模型变得简单。
一个极端是k等于样本数m,则完全没有分类,此时无论输入实例是什么,都只是简单的预测它属于在训练实例中最多的类,模型过于简单。
对于距离的度量,我们有很多的距离度量方式,但是最常用的是欧式距离,即对于两个n维向量x和y,两者的欧式距离定义为:$$D(x,y) = \sqrt{(x_1-y_1)^2 + (x_2-y_2)^2 + ... + (x_n-y_n)^2} = \sqrt{\sum\limits_{i=1}^{n}(x_i-y_i)^2} $$
大多数情况下,欧式距离可以满足我们的需求,我们不需要再去操心距离的度量。
当然我们也可以用他的距离度量方式。比如曼哈顿距离,定义为:$$D(x,y) =|x_1-y_1| + |x_2-y_2| + ... + |x_n-y_n| =\sum\limits_{i=1}^{n}|x_i-y_i| $$
更加通用点,比如闵可夫斯基距离(Minkowski Distance),定义为:$$D(x,y) =\sqrt[p]{(|x_1-y_1|)^p + (|x_2-y_2|)^p + ... + (|x_n-y_n|)^p} =\sqrt[p]{\sum\limits_{i=1}^{n}(|x_i-y_i|)^p} $$
可以看出,欧式距离是闵可夫斯基距离距离在p=2时的特例,而曼哈顿距离是p=1时的特例。
2. KNN算法蛮力实现
从本节起,我们开始讨论KNN算法的实现方式。首先我们看看最想当然的方式。
既然我们要找到k个最近的邻居来做预测,那么我们只需要计算预测样本和所有训练集中的样本的距离,然后计算出最小的k个距离即可,接着多数表决,很容易做出预测。这个方法的确简单直接,在样本量少,样本特征少的时候有效。但是在实际运用中很多时候用不上,为什么呢?因为我们经常碰到样本的特征数有上千以上,样本量有几十万以上,如果我们这要去预测少量的测试集样本,算法的时间效率很成问题。因此,这个方法我们一般称之为蛮力实现。比较适合于少量样本的简单模型的时候用。
既然蛮力实现在特征多,样本多的时候很有局限性,那么我们有没有其他的好办法呢?有!这里我们讲解两种办法,一个是KD树实现,一个是球树实现。
3. KNN算法之KD树实现原理
KD树算法没有一开始就尝试对测试样本分类,而是先对训练集建模,建立的模型就是KD树,建好了模型再对测试集做预测。所谓的KD树就是K个特征维度的树,注意这里的K和KNN中的K的意思不同。KNN中的K代表最近的K个样本,KD树中的K代表样本特征的维数。为了防止混淆,后面我们称特征维数为n。
KD树算法包括三步,第一步是建树,第二部是搜索最近邻,最后一步是预测。
3.1 KD树的建立
我们首先来看建树的方法。KD树建树采用的是从m个样本的n维特征中,分别计算n个特征的取值的方差,用方差最大的第k维特征$n_k$来作为根节点。对于这个特征,我们选择特征$n_k$的取值的中位数$n_{kv}$对应的样本作为划分点,对于所有第k维特征的取值小于$n_{kv}$的样本,我们划入左子树,对于第k维特征的取值大于等于$n_{kv}$的样本,我们划入右子树,对于左子树和右子树,我们采用和刚才同样的办法来找方差最大的特征来做更节点,递归的生成KD树。
具体流程如下图:
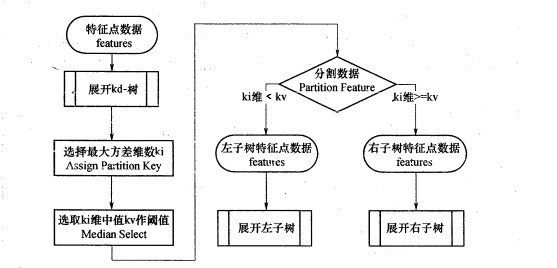
比如我们有二维样本6个,{(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)},构建kd树的具体步骤为:
1)找到划分的特征。6个数据点在x,y维度上的数据方差分别为6.97,5.37,所以在x轴上方差更大,用第1维特征建树。
2)确定划分点(7,2)。根据x维上的值将数据排序,6个数据的中值(所谓中值,即中间大小的值)为7,所以划分点的数据是(7,2)。这样,该节点的分割超平面就是通过(7,2)并垂直于:划分点维度的直线x=7;
3)确定左子空间和右子空间。 分割超平面x=7将整个空间分为两部分:x<=7的部分为左子空间,包含3个节点={(2,3),(5,4),(4,7)};另一部分为右子空间,包含2个节点={(9,6),(8,1)}。
4)用同样的办法划分左子树的节点{(2,3),(5,4),(4,7)}和右子树的节点{(9,6),(8,1)}。最终得到KD树。
最后得到的KD树如下:
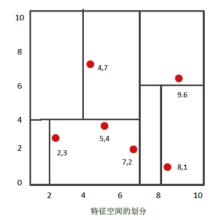
3.2 KD树搜索最近邻
当我们生成KD树以后,就可以去预测测试集里面的样本目标点了。对于一个目标点,我们首先在KD树里面找到包含目标点的叶子节点。以目标点为圆心,以目标点到叶子节点样本实例的距离为半径,得到一个超球体,最近邻的点一定在这个超球体内部。然后返回叶子节点的父节点,检查另一个子节点包含的超矩形体是否和超球体相交,如果相交就到这个子节点寻找是否有更加近的近邻,有的话就更新最近邻。如果不相交那就简单了,我们直接返回父节点的父节点,在另一个子树继续搜索最近邻。当回溯到根节点时,算法结束,此时保存的最近邻节点就是最终的最近邻。
从上面的描述可以看出,KD树划分后可以大大减少无效的最近邻搜索,很多样本点由于所在的超矩形体和超球体不相交,根本不需要计算距离。大大节省了计算时间。
我们用3.1建立的KD树,来看对点(2,4.5)找最近邻的过程。
先进行二叉查找,先从(7,2)查找到(5,4)节点,在进行查找时是由y = 4为分割超平面的,由于查找点为y值为4.5,因此进入右子空间查找到(4,7),形成搜索路径<(7,2),(5,4),(4,7)>,但 (4,7)与目标查找点的距离为3.202,而(5,4)与查找点之间的距离为3.041,所以(5,4)为查询点的最近点; 以(2,4.5)为圆心,以3.041为半径作圆,如下图所示。可见该圆和y = 4超平面交割,所以需要进入(5,4)左子空间进行查找,也就是将(2,3)节点加入搜索路径中得<(7,2),(2,3)>;于是接着搜索至(2,3)叶子节点,(2,3)距离(2,4.5)比(5,4)要近,所以最近邻点更新为(2,3),最近距离更新为1.5;回溯查找至(5,4),直到最后回溯到根结点(7,2)的时候,以(2,4.5)为圆心1.5为半径作圆,并不和x = 7分割超平面交割,如下图所示。至此,搜索路径回溯完,返回最近邻点(2,3),最近距离1.5。
对应的图如下:
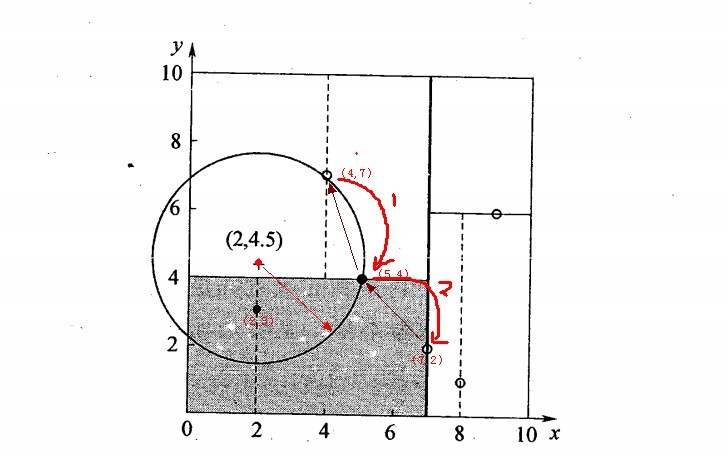
3.3 KD树预测
有了KD树搜索最近邻的办法,KD树的预测就很简单了,在KD树搜索最近邻的基础上,我们选择到了第一个最近邻样本,就把它置为已选。在第二轮中,我们忽略置为已选的样本,重新选择最近邻,这样跑k次,就得到了目标的K个最近邻,然后根据多数表决法,如果是KNN分类,预测为K个最近邻里面有最多类别数的类别。如果是KNN回归,用K个最近邻样本输出的平均值作为回归预测值。
4. KNN算法之球树实现原理
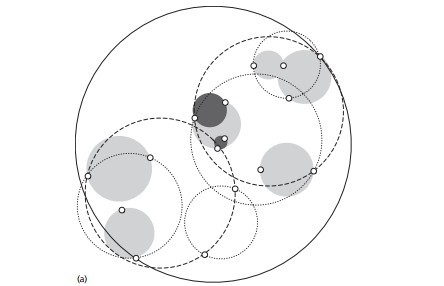
KD树算法虽然提高了KNN搜索的效率,但是在某些时候效率并不高,比如当处理不均匀分布的数据集时,不管是近似方形,还是矩形,甚至正方形,都不是最好的使用形状,因为他们都有角。一个例子如下图:

如果黑色的实例点离目标点星点再远一点,那么虚线圆会如红线所示那样扩大,导致与左上方矩形的右下角相交,既然相 交了,那么就要检查这个左上方矩形,而实际上,最近的点离星点的距离很近,检查左上方矩形区域已是多余。于此我们看见,KD树把二维平面划分成一个一个矩形,但矩形区域的角却是个难以处理的问题。
为了优化超矩形体导致的搜索效率的问题,牛人们引入了球树,这种结构可以优化上面的这种问题。
我们现在来看看球树建树和搜索最近邻的算法。
4.1 球树的建立
球树,顾名思义,就是每个分割块都是超球体,而不是KD树里面的超矩形体。
我们看看具体的建树流程:
1) 先构建一个超球体,这个超球体是可以包含所有样本的最小球体。
2) 从球中选择一个离球的中心最远的点,然后选择第二个点离第一个点最远,将球中所有的点分配到离这两个聚类中心最近的一个上,然后计算每个聚类的中心,以及聚类能够包含它所有数据点所需的最小半径。这样我们得到了两个子超球体,和KD树里面的左右子树对应。
3)对于这两个子超球体,递归执行步骤2). 最终得到了一个球树。
可以看出KD树和球树类似,主要区别在于球树得到的是节点样本组成的最小超球体,而KD得到的是节点样本组成的超矩形体,这个超球体要与对应的KD树的超矩形体小,这样在做最近邻搜索的时候,可以避免一些无谓的搜索。
4.2 球树搜索最近邻
使用球树找出给定目标点的最近邻方法是首先自上而下贯穿整棵树找出包含目标点所在的叶子,并在这个球里找出与目标点最邻近的点,这将确定出目标点距离它的最近邻点的一个上限值,然后跟KD树查找一样,检查兄弟结点,如果目标点到兄弟结点中心的距离超过兄弟结点的半径与当前的上限值之和,那么兄弟结点里不可能存在一个更近的点;否则的话,必须进一步检查位于兄弟结点以下的子树。
检查完兄弟节点后,我们向父节点回溯,继续搜索最小邻近值。当回溯到根节点时,此时的最小邻近值就是最终的搜索结果。
从上面的描述可以看出,KD树在搜索路径优化时使用的是两点之间的距离来判断,而球树使用的是两边之和大于第三边来判断,相对来说球树的判断更加复杂,但是却避免了更多的搜索,这是一个权衡。
5. KNN算法的扩展
这里我们再讨论下KNN算法的扩展,限定半径最近邻算法。
有时候我们会遇到这样的问题,即样本中某系类别的样本非常的少,甚至少于K,这导致稀有类别样本在找K个最近邻的时候,会把距离其实较远的其他样本考虑进来,而导致预测不准确。为了解决这个问题,我们限定最近邻的一个最大距离,也就是说,我们只在一个距离范围内搜索所有的最近邻,这避免了上述问题。这个距离我们一般称为限定半径。
接着我们再讨论下另一种扩展,最近质心算法。这个算法比KNN还简单。它首先把样本按输出类别归类。对于第 L类的$C_l$个样本。它会对这$C_l$个样本的n维特征中每一维特征求平均值,最终该类别所有维度的n个平均值形成所谓的质心点。对于样本中的所有出现的类别,每个类别会最终得到一个质心点。当我们做预测时,仅仅需要比较预测样本和这些质心的距离,最小的距离对于的质心类别即为预测的类别。这个算法通常用在文本分类处理上。
6. KNN算法小结
KNN算法是很基本的机器学习算法了,它非常容易学习,在维度很高的时候也有很好的分类效率,因此运用也很广泛,这里总结下KNN的优缺点。
KNN的主要优点有:
1) 理论成熟,思想简单,既可以用来做分类也可以用来做回归
2) 可用于非线性分类
3) 训练时间复杂度比支持向量机之类的算法低,仅为O(n)
4) 和朴素贝叶斯之类的算法比,对数据没有假设,准确度高,对异常点不敏感
KNN的主要缺点有:
1)计算量大,尤其是特征数非常多的时候
2)样本不平衡的时候,对稀有类别的预测准确率低
3)KD树,球树之类的模型建立需要大量的内存
4)使用懒散学习方法,基本上不学习,导致预测时速度比起逻辑回归之类的算法慢
以上就是KNN算法原理的一个总结,希望可以帮到朋友们,尤其是在用scikit-learn学习KNN的朋友们。
(欢迎转载,转载请注明出处。欢迎沟通交流: liujianping-ok@163.com)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号