wqs二分/Aliens' trick 学习笔记
前言: \(wqs\) 二分是黑龙江神仙王钦石最早在 \(2012\) 年国家集训队论文中提出的一类二分斜率以求凸函数的极值方法,自 \([IOI2016]Aliens\) 在国际上普及。这类问题有一些明显的特征,下文会进行总结。
Section 1. 引入——何为wqs二分?
如下图,我们用一条斜率为 \(p\) 的直线尝试切上凸函数 \(f(x)\) ,在点 \(P(x,f(x))\) 处与上凸壳相切,截距为 \(b\) ,得到函数 \(f(x)\) 的一个值。
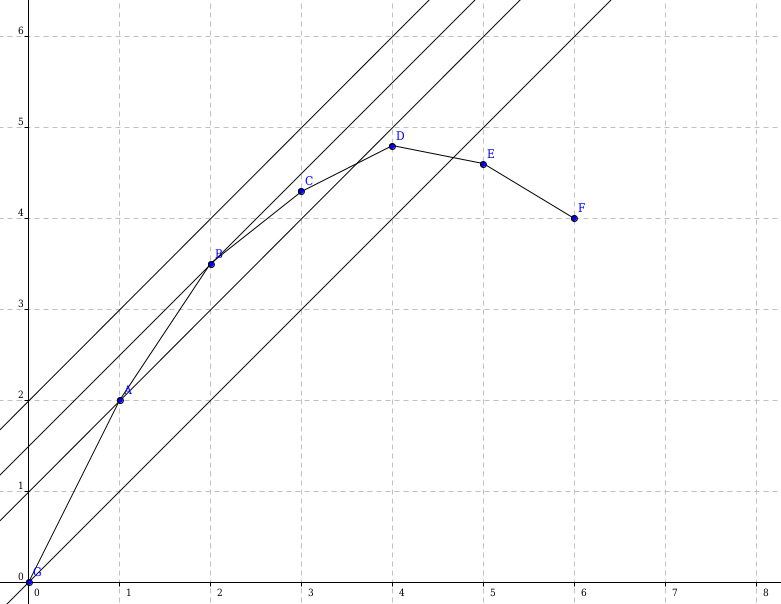
由于函数的凸性质, \(p\) 越小,切点越高(这个比较好理解:离极值越近,相邻两点构成的直线斜率越小),同时截距也会越高,当然 \(p\) 不可能过小,不然切点就会在另一侧了。于是我们二分这个斜率,就可以找到这个函数的极值。
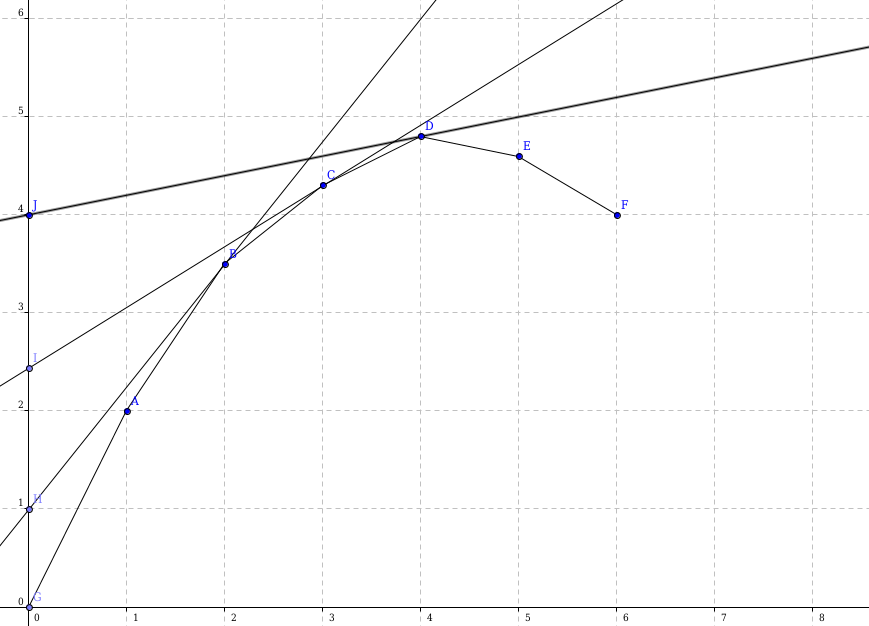
运用这个思想,我们来看一道例题:
例1:[COCI2019]Quiz 试 看 看!
Update on 7.7 改名了 [COCI2018-2019#4]Akvizna
你面临 \(n\) 名参赛者的挑战,最终要将他们全部战胜。
每一轮中,都会淘汰一些选手;你会得到这一轮奖金池中 被淘汰者 除以 这一轮对手总数 比例的奖金。
例如某一轮有 \(10\) 个对手,淘汰了 \(3\) 个,那么你将获得奖金池中 \(\frac{3}{10}\) 的奖金。
假设每一轮的奖金池均为一元,你希望通过恰好 \(k\) 轮赢得比赛,那么你最多可能获得多少奖金呢?
你只需要输出答案保留 \(9\) 位小数即可。
\(1\le k\le n\le 10^5\)
没有 \(k\) 的限制,这题就是一个裸的斜率优化 \(dp\) ,理性感性思考一波,会发现 \(k\) 越大,越容易得到更多奖金,然后试着归纳一下:
设当前有 \(m\) 人,\(1\ or\ 2\) 轮后剩下 \(m-p\) 人,则取划分点 \(m-p\le m-q<m\) ,有:
\(\frac{q}{m}+\frac{p-q}{m-q}=\frac{mp-q^2}{m(m-q)}\ge\frac{mp-pq}{m(m-q)}=\frac{p}{m}\)
于是得到答案 \(ans\) 是关于 \(k\) 的凸函数。
此时我们看截距 \(b\) ,可表示为 \(ans-p\times k\) ,由于我们正好会有 \(k\) 次转移,因此当我们在每次转移中减去斜率 \(p\) ,最终就会得到 \(k\) 时截距 \(b\) ,也对应即 \(ans\) 的最大值。因此,我们在 \(dp\) 转移时增加一个转移常数,并计算最大答案的转移次数,若 \(\le k\)则符合条件,进一步二分,这正是 wqs 二分的核心思想。注意答案要加上 \(p\times k\)
点击查看代码
#include<bits/stdc++.h>
#define int long long
#define double long double
#define inf 1e18
#define N 100005
#define ls k<<1
#define rs k<<1|1
#define mid ((l+r)*0.5)
#define mp make_pair
#define pb push_back
#define pii pair<int,int>
#define fi first
#define se second
#define il inline
#define file(x) freopen(x".in","r",stdin);freopen(x".out","w",stdout);
using namespace std;
il int read(){
int w=0,h=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')h=-h;ch=getchar();}
while(ch>='0'&&ch<='9'){w=w*10+ch-'0';ch=getchar();}
return w*h;
}
const double eps=1e-15;
int n,K,tim[N],q[N],hd,tl;
double dp[N];
double X(int i){return (double)i;}
double Y(int i){return dp[i];}
double Slope(int i,int j){return(Y(i)-Y(j))/(X(i)-X(j));}
bool check(double x){
hd=tl=1;
for(int i=1;i<=n;i++){
while(hd<tl&&Slope(q[hd],q[hd+1])>eps+1.0/i)hd++;
dp[i]=dp[q[hd]]+(double)(i-q[hd])/i-x;tim[i]=tim[q[hd]]+1;
while(hd<tl&&Slope(q[tl],q[tl-1])+eps<Slope(q[tl],i))tl--;
q[++tl]=i;
}
return tim[n]<=K;
}
signed main(){
n=read();K=read();
double l=0.0,r=1e6;
while(l+eps<r){
if(check(mid))r=mid;
else l=mid;
}
r=l;check(mid);
printf("%.9Lf\n",dp[n]+K*mid);
return 0;
}
但有个小问题:我们在二分中设定的限制是不超过k,而题目的要求是恰好k,因此如果答案关于 \(k\) 不单调,这个 \(k\) 实际上可能在凸壳的另一侧,这样做显然无法得到正确答案。
这个问题很好解决:在凸壳另一侧那么用来切凸壳的斜率应该小于 \(0\) ,于是我们把二分的边界扩大到负区域。我们还会发现,二分的限制并不取决于答案,而是取决于转移次数,所以当斜率尝试负区域时,转移次数肯定不会更少,这样二分下去得到的答案就会恰好 \(=k\) 了
可以发现,这类题目有两个明显特征:
恰好 or 不超过 k、答案是关于 \(k\) 的凸函数
Section 2. 进阶——wqs二分常见组合
以下将以几个典型并有思维难度的题目进行讲解。(凸性质感性理解一下,毕竟笔者大多也不会证……)
例2:[IOI2016]Aliens
我们的卫星刚刚通过观测一个遥远的星球发现了外星文明。我们也已经获得了该星球的一个正方形区域的低分辨率照片。这个照片上有许多智能生命的迹象。专家们也已经确定了照片上的 \(n\) 个兴趣点。这些兴趣点被编号为 \(0\) 到 \(n-1\)。现在我们希望拍摄一些能包含全部 \(n\) 个兴趣点的高分辨率照片。
卫星已将低分辨率照片的区域划分成由 \(m \times m\) 个单位正方形的小方格组成的网络。网格的行和列被连续地编号为 \(0\) 到 \(m-1\)(从上到下和从左到右)。我们用坐标 \((s,t)\) 来表示第 \(s\) 行与第 \(t\) 列上的小方格。第 \(i\) 个兴趣点位于小方格 \((r_i,c_i)\) 上,每个小方格子上可以包含任意多个兴趣点。
卫星在一个固定的轨道上运行,而它刚好也直接经过这个网格的主对角线的上方。主对角线就是指在网络中连接左上角和右下角的那条线段。卫星能够在任意的区域上拍摄高分辨率的照片,但必须满足以下条件:
- 拍摄的区域必须是正方形。
- 这个正方形的两个对角(注:变通理解为主对角线)全部包含在网格的主对角线中。
- 网格中的每个小方格或者完全在拍摄范围内,或者完全在拍摄范围外。 卫星最多只能拍摄 \(k\) 张高分辨率照片。
一旦卫星拍摄完成,它将把每个拍摄区域的高分辨率照片传送到地面基站(无论这些区域是否包含兴趣点)。尽管一个小方格可能会被多次拍摄,但每个被拍摄到的小方格上的数据只会被传送一次。
因此,我们必须选择最多 \(k\) 个正方形区域进行拍摄,而且要保证:
- 每个包含至少一个兴趣点的小方格必须被至少拍摄到一次
- 被拍摄到至少一次的小方格数目必须是最小的。
你的任务就是去找出被拍摄到的小方格有可能的最小值。
\(1\le k\le n\le 10^5,m\le 10^6\)
\(2016\) 年 \(wqs\) 二分还没有在竞赛圈普及,因此这题出现在 \(IOI\) 赛场时除中国选手金策通过外几乎所有人都是 \(60\) 分的 \(O(nk)\) 斜率优化 \(dp\) ,后来西方算法圈的 \(Aliens'\ Trick\) 就以此题命名。
但如果会 \(wqs\) 二分,这题基本是一个模板题。
首先很容易想到将点转移到主对角线上的区间,问题转化为二次费用的线段覆盖问题。对于有包含关系的线段来说,只需覆盖最大的一个即可,这里也是一个非常显然的斜率优化,在没有 \(k\) 的情况下,列出转移方程:
然后分类讨论并不好看,令 \(val[i]=[i>0\wedge r_i\ge l_{i+1}](r_i-l_{i+1}+1)^2\) 。容易猜到答案关于 \(k\) 是一个下凸的函数,于是再如上套上一个 \(wqs\) 二分就完事了。
点击查看代码
#include<bits/stdc++.h>
#define int long long
#define double long double
#define inf 1e18
#define N 100005
#define ls k<<1
#define rs k<<1|1
#define mid (((l+r)>>1)+1)
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define pii pair<int,int>
#define il inline
#define file(x) freopen(x".in","r",stdin);freopen(x".out","w",stdout)
using namespace std;
il int read(){
int w=0,h=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')h=-h;ch=getchar();}
while(ch>='0'&&ch<='9'){w=w*10+ch-'0';ch=getchar();}
return w*h;
}
const double eps=1e-11;
struct Alien{int l,r;}A[N],B[N];
int n,m,K,top,q[N],val[N],stp[N],dp[N];
int sqr(int x){return x*x;}
int X(int i){return A[i+1].l;}
int Y(int i){return dp[i]+sqr(A[i+1].l)-val[i];}
double Slope(int i,int j){return(double)(Y(j)-Y(i))/(X(j)-X(i));}
bool check(int x){
int hd=1,tl=1;
for(int i=1;i<=n;i++){
while(hd<tl&&Slope(q[hd],q[hd+1])+eps<=((A[i].r+1)<<1))hd++;
dp[i]=dp[q[hd]]+sqr(A[i].r-A[q[hd]+1].l+1)-val[q[hd]]-x;stp[i]=stp[q[hd]]+1;
if(i<n)while(hd<tl&&Slope(q[tl-1],q[tl])-eps>=Slope(q[tl],i))tl--;
q[++tl]=i;
}
return stp[n]<=K;
}
signed main(){
n=read();m=read();K=read();
for(int i=1;i<=n;i++){
int x=read(),y=read();
B[i].l=min(x,y);B[i].r=max(x,y);
}
sort(B+1,B+n+1,[](Alien x,Alien y){return(x.l==y.l)?x.r>y.r:x.l<y.l;});
for(int i=1,lst=-1;i<=n;i++)
if(B[i].r>lst)A[++top]=B[i],lst=B[i].r;
n=top;
for(int i=2;i<=n;i++)
if(A[i-1].r>=A[i].l)val[i-1]=sqr(A[i-1].r-A[i].l+1);
int l=-1e12,r=0,ans=0;
while(l<r){
if(check(mid))ans=dp[n]+mid*K,l=mid;
else r=mid-1;
}
printf("%lld\n",ans);
return 0;
}
例3:[八省联考2018]林克卡特树
小 L 最近沉迷于塞尔达传说:荒野之息(\(\cal{The\ Legend\ of\ Zelda: Breath\ of\ The\ Wild}\))无法自拔,他尤其喜欢游戏中的迷你挑战。
游戏中有一个叫做LCT的挑战,它的规则是这样子的:现在有一个 \(N\) 个点的树,每条边有一个整数边权 \(v_i\) ,若 \(v_i\ge 0\) ,表示走这条边会获得 \(v_i\) 的收益;若 \(v_i\lt 0\) ,则表示走这条边需要支付 \(-v_i\) 的过路费。小 L 需要控制主角Link切掉Cut树上的恰好 \(K\) 条边,然后再连接 \(K\) 条边权为 \(0\) 的边,得到一棵新的树。接着,他会选择树上的两个点 \(p,q\) ,并沿着树上连接这两点的简单路径从 \(p\) 走到 \(q\) ,并为经过的每条边支付过路费/ 获取相应收益。
海拉鲁大陆之神TemporaryDO想考验一下Link。他告诉Link,如果Link能切掉合适的边、选择合适的路径从而使总收益 - 总过路费最大化的话,就把传说中的大师之剑送给他。
小 L 想得到大师之剑,于是他找到了你来帮忙,请你告诉他,Link能得到的总收益 - 总过路费最大是多少。
\(1\le K<N\le 3\times 10^5\)
一个很显然的性质:切掉的边不会走,不然干嘛切掉。然后树就被分成了一个森林,这时我们可以通过连的边从一棵树走到另一棵树,于是问题转化为求直径最大的 \(K+1\) 棵树的直径和,即在原树上求最大的 \(K+1\) 条不相交的链长的和,这是一个经典的树形 \(dp\) 问题,不考虑 \(K\) 的限制,设 \(dp_{u,0/1/2}\) 为以 \(u\) 为根的子树,且 \(u\) 的度数(准确说应该是儿子中与 \(u\) 相连的个数)为 \(0/1/2\) 的答案,列出转移方程:
最后 \(dp_{u,0}=\max(dp_{u,0},{dp_{u,1}}^*,dp_{u,2})\)
显然 \(K\) 越大答案越大,原问题具有凸性质,然后再次套上 wqs 二分就没了。 一个要注意的地方:转移次数应在一条链结束时计算(上述转移方程标 \(^*\) 处)。
点击查看代码
#include<bits/stdc++.h>
#define int long long
#define inf 1e18
#define N 300005
#define ls k<<1
#define rs k<<1|1
#define mid ((l+r)>>1)
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define pii pair<int,int>
#define il inline
#define file(x) freopen(x".in","r",stdin);freopen(x".out","w",stdout)
using namespace std;
il int read(){
int w=0,h=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')h=-h;ch=getchar();}
while(ch>='0'&&ch<='9'){w=w*10+ch-'0';ch=getchar();}
return w*h;
}
struct Edge{int next,to,val;}edge[N<<1];
int n,K,sum,slp;
int head[N],num;
struct Node{
int val,tim;
bool operator<(const Node&p)const{return val==p.val?tim>p.tim:val<p.val;}
Node operator+(const Node&p)const{return(Node){val+p.val,tim+p.tim};}
Node operator+(const int&p)const{return(Node){val+p,tim};}
Node operator*(const int&p)const{return(Node){val-slp,tim+1};}
}dp[N][3];
void add(int u,int v,int w){
edge[++num].next=head[u];
edge[num].to=v;
edge[num].val=w;
head[u]=num;
}
void dfs(int u,int fa){
dp[u][2]=(Node){-slp,1};
for(int i=head[u];i;i=edge[i].next){
int v=edge[i].to,val=edge[i].val;
if(v==fa)continue;
dfs(v,u);
dp[u][2]=max(dp[u][2]+dp[v][0],(dp[u][1]+dp[v][1]+val)*0);
dp[u][1]=max(dp[u][1]+dp[v][0],dp[u][0]+dp[v][1]+val);
dp[u][0]=max(dp[u][0],dp[u][0]+dp[v][0]);
}
dp[u][0]=max(dp[u][0],max(dp[u][1]*0,dp[u][2]));
}
bool check(int x){
slp=x;
for(int i=1;i<=n;i++)
dp[i][0].val=dp[i][0].tim=dp[i][1].val=dp[i][1].tim=dp[i][2].val=dp[i][2].tim=0;
dfs(1,0);
return dp[1][0].tim<=K;
}
signed main(){
n=read();K=read()+1;
for(int i=2;i<=n;i++){
int u=read(),v=read(),w=read();
add(u,v,w);add(v,u,w);sum+=abs(w);
}
int l=-sum,r=sum,ans=-inf;
while(l<=r){
if(check(mid))ans=mid,r=mid-1;
else l=mid+1;
}
check(ans);
printf("%lld\n",dp[1][0].val+ans*K);
return 0;
}
例4:[MtOI2019]不可视境界线
Rikka坚信,她的父亲在「不可视境界线」中,等待着她的到来。在Rikka的梦里,「不可视境界线」出现了,那是 \(n\) 个圆组成的图形。
具体地,有一个平面直角坐标系,坐标系的 \(x\) 轴上有 \(n\) 个点,第 \(i\) 个点的坐标为 \((x_i,0)\) 。
Rikka以每一个点作为圆心,作了 \(n\) 个半径为 \(r\) 的圆。她本想让你帮她计算这 \(n\) 个圆的面积并,但是这个问题太简单了。
在一番思考后,Rikka想让你计算出选出 \(k\) 个圆后(即删除 \(n-k\) 个圆),圆的面积并的最大值。
对于所有数据,有 \(n,k\leq 10^5\) ,\(r\leq 10^4\) ,\(0\leq x_i\leq 10^9\) ,\(x_i\) 为整数且不重复。保证输入的 \(x_i\) 单调递增。
因为答案太大了,Rikka考虑到你的电脑无法保持高精度,所以只要你的答案与标准答案的 相对误差 小于 \(5\times 10^{-8}\),你的答案即被视为是正确的。
经过误差分析,本题保证使用原生 \(cmath\) 函数不会出错,请注意控制程序精度误差。
圆的面积并是数学问题,掉头 \(baidu\) 搜一搜。
直接做是 \(2D/1D\) 的 \(O(n^3)\) ,无法承受。
套路地上一波 \(wqs\) 二分,这个问题就变成了任选的“太简单了”,容斥面积并?肯定不行。考虑仅算新圆的增量,那么这个增量显然只与决策点有关,这样的话猜猜这个有决策单调性,然后感性理解一下发现真有(严谨证明看 \(disangan233\) 的题解)。这个也比较套路,开个二分队列就完了(这个不会的话可以看 cmd的博客)。
有点卡常 \(+\) 卡精度,可以加几个 \(inline\) 再把 \(eps\) 开小点。
点击查看代码
#include<bits/stdc++.h>
#define int long long
#define double long double
#define inf 1e18
#define N 100005
#define ls k<<1
#define rs k<<1|1
#define mid ((l+r)/2)
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define pii pair<int,int>
#define il inline
#define file(x) freopen(x".in","r",stdin);freopen(x".out","w",stdout)
using namespace std;
il int read(){
int w=0,h=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')h=-h;ch=getchar();}
while(ch>='0'&&ch<='9'){w=w*10+ch-'0';ch=getchar();}
return w*h;
}
const double pi=3.141592653589;
int n,K,R,X[N];
int q[N],hd,tl,tim[N],pos[N];
double Area,Sq[N],dp[N];
il double Sqr(int i,int j){return dp[i]+((X[j]-X[i]>=R+R)?(Area):(Sq[X[j]-X[i]]));}
il int Bound(int i,int j){
int l=j,r=n+1;
while(l+1<r){
if(Sqr(j,mid)>Sqr(i,mid))r=mid;
else l=mid;
}
return r;
}
il bool check(double x){
q[hd=tl=1]=0;
for(int i=1;i<=n;i++){
while(hd<tl&&pos[hd+1]<=i)hd++;
dp[i]=Sqr(q[hd],i)-x;tim[i]=tim[q[hd]]+1;
while(hd<tl&&Bound(q[tl],i)<=pos[tl])tl--;
q[++tl]=i;pos[tl]=Bound(q[tl-1],i);
}
return tim[n]<=K;
}
signed main(){
n=read();K=read();R=read();Area=pi*R*R;
for(int i=1;i<=n;i++)X[i]=read();X[0]=-inf;
for(int i=1;i<=R+R;i++)Sq[i]=(pi-acos(0.5*i/R)*2)*R*R+sqrt(R*R-0.25*i*i)*i;
double l=0,r=Area,eps=1e-10;
while(l+eps<r){
if(check(mid))r=mid;
else l=mid;
}
check(r);
printf("%.8Lf",dp[n]+K*r);
return 0;
}
由此我们发现 \(wqs\) 二分的又一特点:消去 \(k\) 限制后,子问题具有明显的阶段性,每次决策能够快速计算。
Section 3. 深究——Things Grow Worse!
这里有一些很好的 \(wqs\) 二分题,知识的缝合结合性强,会尽量给出证明。
例5:[IOI2000]邮局 加强版
高速公路旁边有 \(n\) 个村庄。高速公路表示为整数轴,每个村庄的位置用单个整数坐标 \(a_i\) 标识。两个位置之间的距离是其整数坐标差的绝对值。
现在要建立 \(m\) 个邮局,邮局将建在一些,但不一定是所有的村庄中。为了建立邮局,应选择他们建造的位置,使每个村庄与其最近的邮局之间的距离总和最小。
你要编写一个程序,已知村庄的位置和邮局的数量,计算每个村庄和最近的邮局之间所有距离的最小可能的总和。
\(1\le m\le n\le 5\times10^5,a_i\le 10^6\)
弱化版 \(1.0\) :山区建小学(很弱智的一个区间 \(dp\) 不必多说了吧……)
弱化版 \(2.0\) :[IOI2000]邮局
在一个区间内取一点,使区间内所有点到这个点的距离之和最小,显然取中位数。于是我们得到一个区间的计算答案函数:
int Calc(int l,int r){
int mid=(l+1+r)>>1;
return(sum[r]-sum[mid])-a[mid]*(r-mid)+a[mid]*(mid-l)-(sum[mid]-sum[l]);//这里为了避免负下标 l 预先减 1
}
这时想到也许会有决策单调性,考虑用四边形不等式证明:
\((1)-(2)\) 得
满足四边形不等式,因此决策具有单调性。用二分队列维护即可做到 \(O(nm\log(n))\)
看回加强版,有 \(m\) 的限制,考虑 \(wqs\) 二分。凸性很好证明:在 \(m\) 的最优解中新增一个邮局,至少会减少邮局所在位置的花费,所以 \(m+1\) 的答案必然小于 \(m\) 的答案。然后结合上述做法即可做到 \(O(n\log^2n)\)
点击查看代码
#include<bits/stdc++.h>
#define int long long
#define inf 1e9
#define N 500005
#define ls k<<1
#define rs k<<1|1
#define mid ((l+r)>>1)
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define pii pair<int,int>
#define il inline
#define file(x) freopen(x".in","r",stdin);freopen(x".out","w",stdout)
using namespace std;
il int read(){
int w=0,h=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')h=-h;ch=getchar();}
while(ch>='0'&&ch<='9'){w=w*10+ch-'0';ch=getchar();}
return w*h;
}
int n,m,a[N],sum[N],dp[N],tim[N];
int q[N],pos[N],hd,tl;
il int Calc(int l,int r){
int pos=(l+1+r)>>1;
return(sum[r]-sum[pos])-a[pos]*(r-pos)+a[pos]*(pos-l)-(sum[pos]-sum[l]);
}
il int Bound(int i,int j){
int l=j,r=n+1;
while(l+1<r)if(dp[j]+Calc(j,mid)<=dp[i]+Calc(i,mid))r=mid;else l=mid;
return r;
}
il bool check(int x){
q[hd=tl=1]=0;
for(int i=1;i<=n;i++){
while(hd<tl&&pos[hd+1]<=i)hd++;
dp[i]=dp[q[hd]]+Calc(q[hd],i)-x;tim[i]=tim[q[hd]]+1;
while(hd<tl&&Bound(q[tl],i)<=pos[tl])tl--;
q[++tl]=i;pos[tl]=Bound(q[tl-1],i);
}
return tim[n]>=m;
}
signed main(){
n=read();m=read();
for(int i=1;i<=n;i++)a[i]=read();
sort(a+1,a+n+1);
for(int i=1;i<=n;i++)sum[i]=sum[i-1]+a[i];
int l=-inf,r=0,ans=114514;
while(l<=r){
if(check(mid))ans=mid,l=mid+1;
else r=mid-1;
}
check(ans);
printf("%lld\n",dp[n]+m*ans);
return 0;
}
例6:[PA2013]Raper / CF802O April Fool's Problem (hard)
你需要生产 \(k\) 张光盘。每张光盘都要经过两道工序:先在 \(A\) 工厂进行挤压,再送到 \(B\) 工厂涂上反光层。
你知道每天 \(A、B\) 工厂分别加工一张光盘的花费。你现在有 \(n\) 天时间,每天可以先送一张光盘到 \(A\) 工厂(或者不送),然后再送一张已经在 \(A\) 工厂加工过的光盘到 \(B\) 工厂(或者不送),每家工厂一天只能对一张光盘进行操作,同一张光盘在一天内生产出来是允许的。我们假定将未加工的或半成品的光盘保存起来不需要费用
求生产出 \(k\) 张光盘的最小花费。
\(1\le k\le n\le 5\times10^5,a_i,b_i\le10^9\)
子问题是经典老鼠进洞模型的变形,考虑用增量法建图。
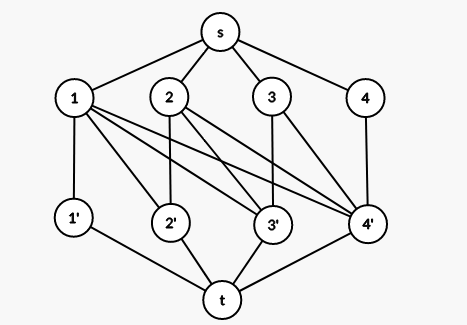
例如现在加入 \(4\) 和 \(4'\) ,在这张图中试着画一下流法,有:
\(s\to 4\to 4'\to t\)
\(s\to 1\to 4'\to 3\to s\)
\(s\to 1\to 4'\to t\to 3'\to 3\to s\)
第一种是常规流法,第二种可看做将原本在第 \(x\) 天在 \(A\) 工厂加工的光盘改到第 \(y\) 天加工,也即修改 \(x,y\) 对应的 \(B\) ,第三种可看做同时修改两次加工的时间,但这种流法并不合法,因为如果有以后另一对 \(A_i,B_j\) 小于当前决策,而当前选择的是当前最优的 \(A\) (不然 \(B\) 就会匹配到 \(A_i\) ),仅修改 \(B\) 为 \(B_j\) 必定不劣。
根据 \(EK\) 算法,增广路长度单调不降,因此费用是关于流量的凸函数,保证了 \(wqs\) 二分的正确性,同时,由于原问题有流量限制,第一种流法可能不合法,用 \(wqs\) 二分消除 \(k\) 的限制之后正好也保证了模拟费用流的正确性。(所以优势互补了属于是?)
点击查看代码
#include<bits/stdc++.h>
#define int long long
#define inf 1e18
#define N 500005
#define ls k<<1
#define rs k<<1|1
#define mid ((l+r)>>1)
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define pii pair<int,int>
#define il inline
#define file(x) freopen(x".in","r",stdin);freopen(x".out","w",stdout)
using namespace std;
il int read(){
int w=0,h=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')h=-h;ch=getchar();}
while(ch>='0'&&ch<='9'){w=w*10+ch-'0';ch=getchar();}
return w*h;
}
int n,K,A[N],B[N],val,res,tim;
bool check(int x){
res=tim=0;
priority_queue<pii,vector<pii>,greater<pii> >q;
for(int i=1;i<=n;i++){
q.push(mp(A[i],0));
if(B[i]-x<=-q.top().fi){
res+=B[i]-x+q.top().fi;
if(!q.top().se)tim++;
q.pop();q.push(mp(-B[i]+x,1));
}
}
return tim>=K;
}
signed main(){
n=read();K=read();
for(int i=1;i<=n;i++)A[i]=read(),val+=A[i];
for(int i=1;i<=n;i++)B[i]=read(),val+=B[i];
int l=0,r=val,ans=114514;
while(l<=r){
if(check(mid))ans=mid,r=mid-1;
else l=mid+1;
}
check(ans);
printf("%lld\n",res+ans*K);
return 0;
}
例7:CF720F Array Covering
给定一个长度为 \(n\) 的序列 \(a\) 。
你需要选出 \(k\) 个不同的子序列 \([l_i, r_i]\) ,使得它们的并为 \([1, n]\) ,求子序列和的最大值。
\(1\le n\le 10^5,1\le k\le \frac{n(n+1)}{2},-5\times10^4\le a_i\le 5\times 10^4\)
闲扯: \(\_sys\) 神找到了一堆结论,然后——码了 \(10k\) 。
首先这题类似于CF1034D,可以用二分求解第 \(k\) 大的子序列,并且会发现 \(\_sys\) 的那些结论,这也是官方的解法,官方在题解里邪恶地提了一嘴:
但如果从另一个角度思考,其实这题并不难写。
大胆猜测答案有凸性质,那么问题转化为任选一些子序列使得至少覆盖每个元素一次,每次选有一定代价的最大收益。考虑 \(dp\) ,令 \(dp_i\) 为覆盖 \(1\sim i\) 的所有元素的最大收益,首先用 \(two\ pointers\) 选上所有收益为正的区间,并记录所选的最小左端点 \(pos_i\) ,那么只要 \(i\) 从 \(j\le pos_i-1\) 转移过来就不会存在空隙,有空隙则先记着,第二阶段是保证每个元素都被覆盖,从可行的位置选择最大的一个转移即可。
证明?好像还没人会证。
点击查看代码
#include<bits/stdc++.h>
#define int long long
#define inf 1000000000000000000
#define N 100005
#define ls k<<1
#define rs k<<1|1
#define mid ((l+r)>>1)
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define pii pair<int,int>
#define il inline
#define fir(x) tmp[x].fi
#define sec(x) tmp[x].se
#define file(x) freopen(x".in","r",stdin);freopen(x".out","w",stdout)
using namespace std;
il int read(){
int w=0,h=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')h=-h;ch=getchar();}
while(ch>='0'&&ch<='9'){w=w*10+ch-'0';ch=getchar();}
return w*h;
}
struct Node{
int val,tim;
Node operator+(const Node&p)const{return(Node){val+p.val,tim+p.tim};}
Node operator-(const Node&p)const{return(Node){val-p.val,tim-p.tim};}
bool operator<(const Node&p)const{return val==p.val?tim<p.tim:val<p.val;}
}res,dp[N],f[N];
int n,K,a[N],sum[N],pos[N];
pii tmp[N];
template<typename T>struct Fenwick{
T c[N],res,base;
il void Update(T&a,T b,int t){(t==1)?(a=a+b):((t==2)?(a=min(a,b)):(a=max(a,b)));}
il void add(int x,T y,int t){for(;x<=n;x+=x&(-x))Update(c[x],y,t);}
il T ask(int x,int t){for(res=base;x;x-=x&(-x))Update(res,c[x],t);return res;}
il void clear(int t){for(int i=1;i<=n;i++)c[i]=base;}
};Fenwick<int>tr[3];Fenwick<Node>rt[2];
il bool check(int x){
for(int i=0;i<=1;i++)rt[i].clear(3);
for(int i=0;i<=2;i++)tr[i].clear(i/2+1);
int j=1;res=(Node){0,0};
for(int i=1;i<=n;i++){
while(j<=n&&fir(j)<=fir(i)-x){
tr[0].add(sec(j),1,1);
tr[1].add(sec(j),fir(j),1);
tr[2].add(sec(j),sec(j),2);
j++;
}
pos[sec(i)]=tr[2].ask(sec(i)-1,2);
dp[sec(i)].tim=tr[0].ask(sec(i)-1,1);
dp[sec(i)].val=fir(i)*dp[sec(i)].tim-tr[1].ask(sec(i)-1,1)-x*dp[sec(i)].tim;
if(fir(i)>=x)dp[sec(i)]=dp[sec(i)]+(Node){fir(i)-x,1},pos[sec(i)]=0;
pos[sec(i)]=min(pos[sec(i)],sec(i));res=res+dp[sec(i)];
}
int lst=0;
for(int i=1;i<=n;i++){
Node a=rt[0].ask(max(0ll,pos[i]-1),3),b=rt[1].ask(min(n,n-pos[i]+1),3);
a=a+(Node){sum[i]-x,1};b=max(b,(pos[i]==0)?(Node){0,0}:(Node){sum[i]-x,1});
f[i]=max(a,b);
lst=min(lst,sum[i]);
rt[1].add(n-i+1,f[i],3);
rt[0].add(i,f[i]-(Node){lst,0},3);
}
res=res+f[n];
return res.tim>=K;
}
signed main(){
tr[0].base=tr[1].base=0;tr[2].base=inf;
rt[0].base=rt[1].base=(Node){-inf,-inf};
n=read();K=read();
for(int i=1;i<=n;i++)a[i]=read(),sum[i]=sum[i-1]+a[i],tmp[i]=mp(sum[i],i);
sort(tmp+1,tmp+n+1);
int l=-inf,r=inf,ans=114514;
while(l<=r){
if(check(mid))ans=mid,l=mid+1;
else r=mid-1;
}
check(ans);
printf("%lld\n",res.val+K*ans);
return 0;
}
Section 4: 总结——wqs二分的应用范畴和一些细节
上文我们有总结 wqs 二分的特征:恰好 or 不超过 k、答案是关于 k 的凸函数、子问题具有明显的阶段性,每次决策能够快速计算。前两点其实很容易发现,然而第三点却往往被忽视,因而想偏。
\(wqs\) 二分能解决大多数具有凸性质的限制条件,这个一定要视情况而定,不能陷入思维定式,比如CF1034D是很明显的 \(wqs\) 二分形式,答案具有单调性,但仔细思考会发现很难确定所选区间,反而不如普通的二分答案结合其他算法可以快速求解,又如[NOI2019]序列,同样可以 \(wqs\) 二分,但效率低下,完全比不上虽思维难度更高的正解模拟费用流(当然,考场上拿分第一)。
常见的应用还是优化一类有 \(k\) 限制的dp,但有时也会结合一些较为困难、高级的算法,灵活选择与运用才是重点。
其实在 wqs 二分中,会产生许多问题,例如在例1中提到的恰好与不超过,这里还有一些典型的细节,会一一给出证明或解决。
Question 1: 如果凸壳上出现连续一段与答案在同一直线上的点怎么办?
如图:这种情况下,二分可能会得到这一段上最高的绿点,但正确答案是某个红点,这种情况 \(wqs\) 二分并不能确保。
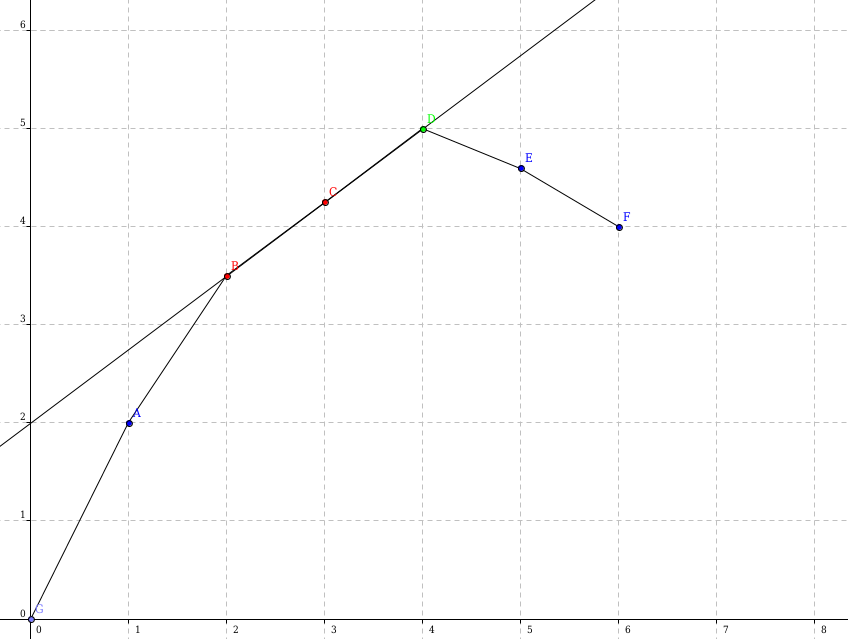
考虑到这些点的性质,实际上这些点只是相差了若干零收益的决策,所以只要在求解子问题时让 \(k\) 尽量大即可。
Question 2: 为什么斜率可以直接二分整数?
这个很好解释:答案是整数,子问题的答案也是整数, \(k\) 也是整数,即凸包上每一段斜率都是整数,所以斜率二分整数就行(差不多就这样理解吧……)。
当然答案是浮点数的话要保证时间就只能用精度换了……
Question 3: 如何确定wqs二分的边界和判定?
首先明确,边界越宽松肯定越好,再就是看答案是上凸还是下凸以确定斜率的正负性,边界大小取决于答案的大小。判定也与凸的方向有关,这个真的不好说,按照题目确定,毕竟有时你以为的下凸壳可能是上凸壳的右半边……
参考资料:
https://zhuanlan.zhihu.com/p/340514421
http://www.doc88.com/p-949564862405.html
https://www.luogu.com.cn/blog/command-block/dp-di-jue-ce-dan-diao-xing-you-hua-zong-jie
https://www.luogu.com.cn/blog/command-block/mu-ni-fei-yong-liu-xiao-ji
(话说后面两个为啥要放进来……


 浙公网安备 33010602011771号
浙公网安备 33010602011771号