Matlab regression

 

% linear regression
% least squares fitting a straight line
load LinearRegressData.mat
plot(x,y,'.')
X=[ones(size(x)),x];
a=X\y

a =

    5.2745
    0.9950
clear
load jump.mat
plot(x,y,'.')
X=[ones(size(x)),x];
a=X\y

a =

   -0.0095
    0.7465
Y=-0.0095 + 0.7465*x;
plot(x,Y,'.')
x1=x;
x2=x.^2;
x3=x.^3;
X=[ones(size(x)),x1,x2,x3];
a=X\y

a =

   -0.0226
    1.3906
    0.0389
   -1.0536
yp=X*a;
plot(x,y,'o',x,yp,'-')
% weighted factors in linear regression
hold on
indx=find(x>0);
X(indx,:)=X(indx,:)/10;
yw=y;
yw(indx)=yw(indx)/10;
aw=X\yw;
ypw=aw(1)+aw(2)*x;
plot(x,ypw,'g-')
clear
load DIC_O2.mat
x=DIC;
y=O2;
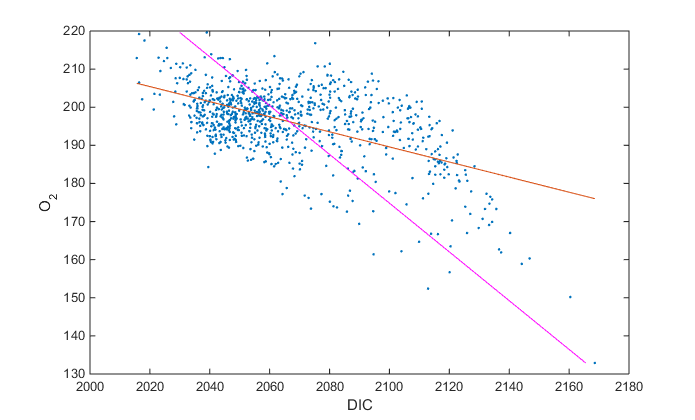
plot(x,y,'.')
xlabel('DIC')
ylabel('O_2')
X=[ones(size(x)),x];
a=X\y;
hold on
yp=X*a;
plot(x,yp,'-')
X=[ones(size(x)),x];
Y=[ones(size(x)),y];
b=Y\x;
xp=Y*b;
plot(xp,y,'m-')

　　

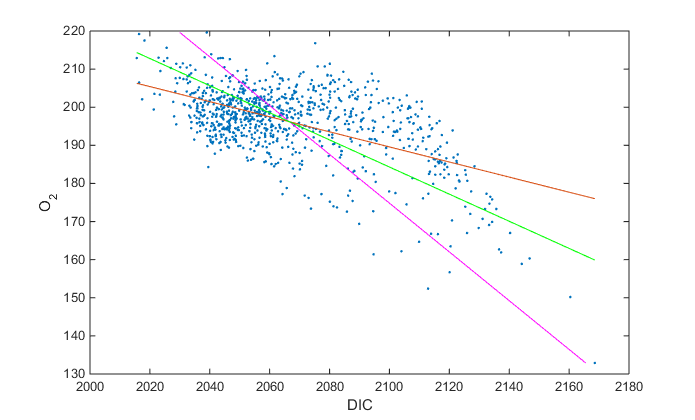
>> % type 2 regression
>> c(2)=sqrt(a(2)/b(2))

c =

         0    0.3559

>> c(2)=-c(2)

c =

         0   -0.3559

>> c(1)=mean(y)-c(2)*mean(x)

c =

  931.6370   -0.3559
>> yII=c(1)+c(2)*x;
>> plot(x,yII,'g-')

% multidimensional regression

　　

  

 

 

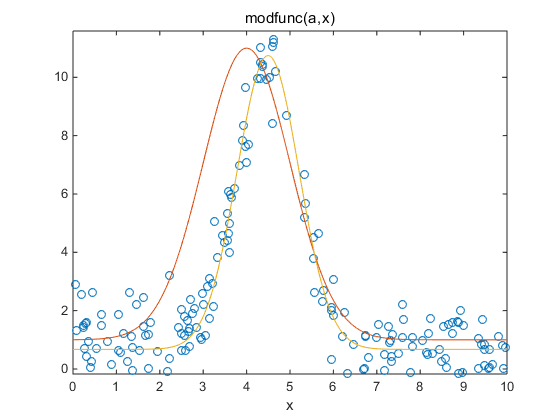
function y=modfunc(a,x)
y=a(1)+a(2)*exp(-(x-a(3)).^2./(2.*a(4).^2));

　　

>> load gauss_data.mat
>> plot(x,y,'o')
>> a0=[1,10,4,1];
>> hold on
>> ezplot(@(x)modfunc(a0,x),[0,10])
>> a=nlinfit(x,y,@modfunc,a0)

a =

    0.6731   10.0709    4.4948    0.7142

>> ezplot(@(x)modfunc(a,x),[0,10])
>> [a,R,J,CovB]=nlinfit(x,y,@modfunc,a0);

    >> err=sqrt(diag(CovB))

err =

0.0828
0.2318
0.0216
0.0202