3 非线性方程求根

3 非线性方程求根

3.1 基本定义

求解非线性方程的根，即求解高次方程或超越方程的根，这类方程没有固定的求根公式。一般的非线性方程形式上可以表示为：

\[f(x)=0 \]

定义3.1：如果\(p\)满足\(f(p)=0\)，则称\(p\)是方程的根或函数的零点。如果\(f(x)\)可以被分解为以下形式：

\[f(x)=(x-p)^mh(x)\quad\text{and}\;\lim\limits_{x\rightarrow p}h(x)\ne0 \]

当\(m>1\)时，我们称\(p\)是\(f(x)=0\)的m重根。

定理3.1：设\(f(x)\in{C^m[a,b]}\)，则\(p\in{(a,b)}\)是\(f(x)\)的m重根，当且仅当

\[f(p)=f'(p)=\cdots=f^{(m-1)}(p)=0\;\text{and}\;f^{(m)}(p)\ne0 \]

上述定理可通过泰勒展开证明。

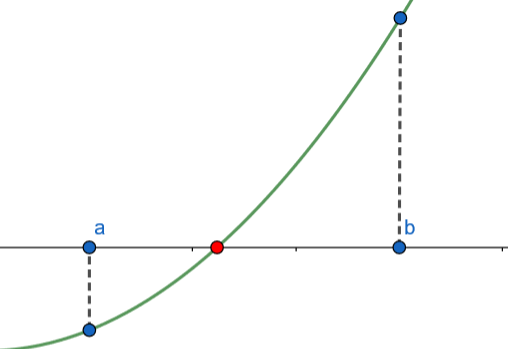
定义3.2：若区间\([a,b]\)含有方程\(f(x)=0\)的根，则称该区间为方程的含根区间。若是区间中仅含一个根，则称该区间为隔根区间。

一般来说，对于连续函数而言，可以通过介值定理判定一个区间内是否含有方程的根（\(f(a)f(b)<0\)），接着再由函数的单调性判定是否根唯一。

3.2 二分法

原理：若\(f(x)\in C[a,b]\)，并且\(f(a)f(b)\lt0\)，则\(f(x)\)在\((a,b)\)上至少存在一个根。

计算过程：

1. 令\(k=0\)，给定初始区间\((a_0,b_0)\)，满足\(f(a_0)f(b_0)<0\)（否则根就在区间端点上）
2. 计算\(x_k=(a_k+b_k)/2\)
3. 如果\(f(x_k)=0\)或\(|b_k-a_k|/2<\varepsilon\)，则\(x_k\)就是所要求的根；
4. 如果\(f(a_k)f(x_k)<0\)，令\(a_{k+1}=a_k,b_{k+1}=x_k,k=k+1\)，返回2
5. 如果\(f(b_k)f(x_k)<0\)，令\(a_{k+1}=x_k,b_{k+1}=b_k,k=k+1\)，返回2

当二分法执行k步之后：

\[|x-x_k|\le\frac{|b_k-a_k|}{2}=\frac{b-a}{2^{k+1}} \]

因此可以使用区间的长度来估计精度。

二分法的缺点：

二分法虽然实现简单，但收敛速度较慢，其收敛速度相当于一个\(1/2\)为公比的等比级数，一般可以用二分法初步确定根的区间。对于偶数阶重根（如\((x-a)^2=0\)）和复数根则无法使用二分法求解。

3.3 不动点迭代

不动点迭代的基本思想是构造一个不动点方程，即将原来的方程\(f(x)=0\)，等价变换为\(x=\varphi(x)\)的形式，其中\(\varphi(\cdot)\)是压缩映射函数。然后通过迭代格式：\(x_{k+1}=\varphi(x_k)\)进行迭代，给定初始值\(x_0\)后，即可迭代收敛到\(\varphi(\cdot)\)的不动点，也就是我们所要求的根。这是因为：

\[x^*=\lim_{k\rightarrow\infty}x_{k+1}=\lim\varphi(x_k)=\varphi(\lim_{}x_k)=\varphi(x^*) \]

迭代过程的示意图如下：

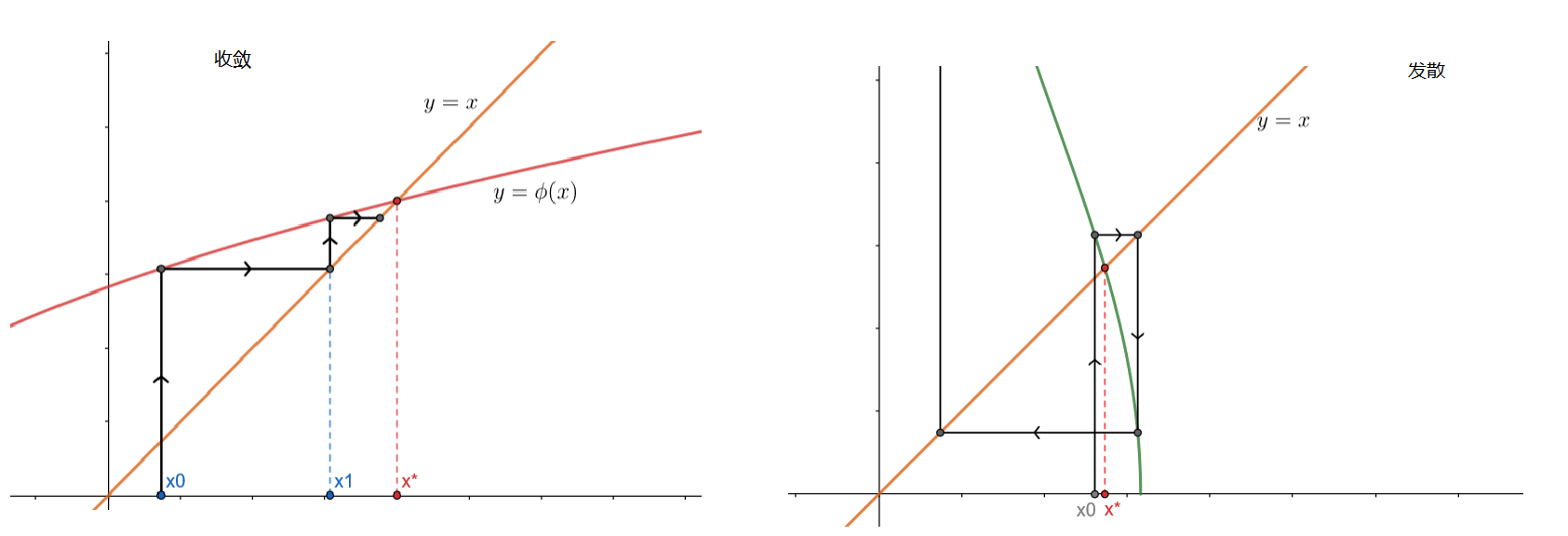
左侧图片是迭代收敛的情况，其中\(p_0=\phi(x_0),x_1=p_0,p_1=\phi(x_1)\)。相当于是沿着直线\(y=x\)向根逼近。右侧图片则是不收敛的情况。

例如：求解方程\(f(x)=x^3+4x^2-10=0\)在\((1,2)\)内的根，具有以下几种迭代格式：

\[\begin{aligned} &1.\;x=x^3+4x^2-10+x\qquad&\text{divergence}\\ &2.\;x=\sqrt{\frac{10}{x}-4x}&\text{divergence}\\ &3.\;x=\frac{1}{2}\sqrt{(10-x^3)}&\text{convergence}\\ &4.\;x=\sqrt{\frac{10}{4+x}}&\text{convergence}\\ \end{aligned} \]

因此，对于相同的方程可以有不同的迭代格式。然而这些格式有些是发散的，有些是收敛的。并且对于收敛的迭代而言，其收敛速度也不尽相同。

之前已经证明，如果\((X,d)\)是一个完备度量空间，且映射\(g:X\rightarrow X\)是集合\(X\)上的一个压缩映射，那么\(g\)有唯一不动点。因此，我们的目标自然是找到一个合适的压缩映射函数。

定理3.2：如果\(\varphi(x)\in{C[a,b]}\)，并满足以下条件：

1. 对于任意\(x\in[a,b]\)，有\(a\le\varphi(x)\le b\)
2. 存在正数\(0\le L<1\)，并且\(\forall\;x_1,x_2\in[a,b]\)，都有\(|\varphi(x_1)-\varphi(x_2)|\le L|x_1-x_2|\)成立

则根据压缩映射定理，只要\(x_0\in[a,b]\)，那么迭代过程\(x_{k+1}=\varphi(x_k)\)必然收敛到该压缩映射的不动点，也就是我们所要求的根。

证明：如果\(\varphi(a)=a\)或者\(\varphi(b)=b\)，即\(a\)或\(b\)是\(\varphi(x)\)的不动点，即我们所要求的根。否则根据条件1，可构造函数\(h(x)=\varphi(x)-x\)并且满足如下条件：

\[h(a)=\varphi(a)-a>0\\h(b)=\varphi(b)-b<0 \]

根据介值定理可知，存在\(x^*\in(a,b)\)使得\(h(x^*)=\varphi(x^*)-x^*=0\)，即\(x^*\)是\(\varphi(x)\)的不动点。

\[|x_{k+1}-x^*|=|\varphi(x_k)-\varphi(x^*)|\le L|x_k-x^*| \]

最终可以得到：\(|x_k-x^*|\le L^k|x_0-x^*|\)，因此

\[\lim_{k\rightarrow\infty}|x_k-x^*|\le\lim_{k\rightarrow\infty}L^k|x_0-x^*|=0 \]

所以\(\lim{x_k}=x^*\)，即根的存在性得到证明。

根据条件2可知，\(\varphi(\cdot)\)实际上就是区间\([a,b]\)上的压缩映射函数，根据第二章关于压缩映射函数的证明可知该不动点\(x^*\)是唯一的。至此，我们证明了根的存在性和唯一性。

此外，根据条件2，\(|x_{k+1}-x_k|=|\varphi(x_k)-\varphi(x_{k-1})|\le L|x_k-x_{k-1}|\)，所以\(|x_{k+1}-x_k|\le L^k|x_1-x_0|\)。对于任意正整数\(p\)有

\[\begin{split} |x_{k+p}-x_k|&\le|x_{k+p}-x_{k+p-1}|+|x_{k+p-1}-x_{k+p-2}|+\cdots+|x_{k+1}-x_k|\\ &\le(L^{k+p-1}+L^{k+p-2}+\cdots+L^k)|x_1-x_0|\\ &\le\frac{L^k}{1-L}|x_1-x_0| \end{split} \]

因为\(p\rightarrow+\infty\)时，\(x_{k+p}\rightarrow x^*\)，所以

\[|x^*-x_k|\le\frac{L^k}{1-L}|x_1-x_0| \]

此外

\[\begin{split} |x^*-x_k|&=|x^*-x_{k+1}+x_{k+1}-x_k|\\ &\le|x^*-x_{k+1}|+|x_{k+1}-x_k|\\ &\le L|x^*-x_{k}|+L|x_{k}-x_{k-1}| \end{split} \]

经过移项可以得到

\[|x^*-x_k|\le\frac{L}{1-L}|x_k-x_{k-1}| \]

所以我们可以令\(|x_k-x_{k-1}|<\varepsilon\)来控制解的迭代次数（精度）。

对于定理3.2而言，关键是找到区间\([a,b]\)上的压缩映射函数，如果

\[\forall\;x\in[a,b],\exists\;L\in[0,1)\quad|\varphi’(x)|\le L<1 \]

那么\(\varphi(x)\)就是该区间上的一个压缩映射函数，根据拉格朗日中值定理可以很容易得到：

\[\forall\;x_1,x_2\in[a,b]\quad|\varphi(x_1)-\varphi(x_2)|=|\varphi'(\xi)||x_1-x_2|\le L|x_1-x_2| \]

其中\(\xi\)在\(x_1\)和\(x_2\)之间。

3.4 牛顿迭代法

设\(x_k\)是\(f(x)=0\)的一个近似根，将\(f(x)\)在\(x_k\)处作泰勒展开

\[f(x)=f(x_k)+f'(x_k)(x-x_k)+\frac{f''(x_k)}{2!}(x-x_k)^2+\cdots \]

若选择前两项来代替\(f(x)\)，称为\(f(x)\)线性化，则得到近似的线性化方程

\[f(x)\approx f(x_k)+f'(x_k)(x-x_k)=0 \]

若\(f(x_k)\ne0\)，将上述式子变成

\[x=x_k-\frac{f(x_k)}{f'(x_k)} \]

写成迭代的形式，如下

\[x_{k+1}=x_k-\frac{f(x_k)}{f'(x_k)} \]

牛顿迭代法具有很直观的几何意义，如下图所示，从\(x_0\)点处开始做切线，然后通过切线与x轴的交点来逼近零点\(x^*\)：

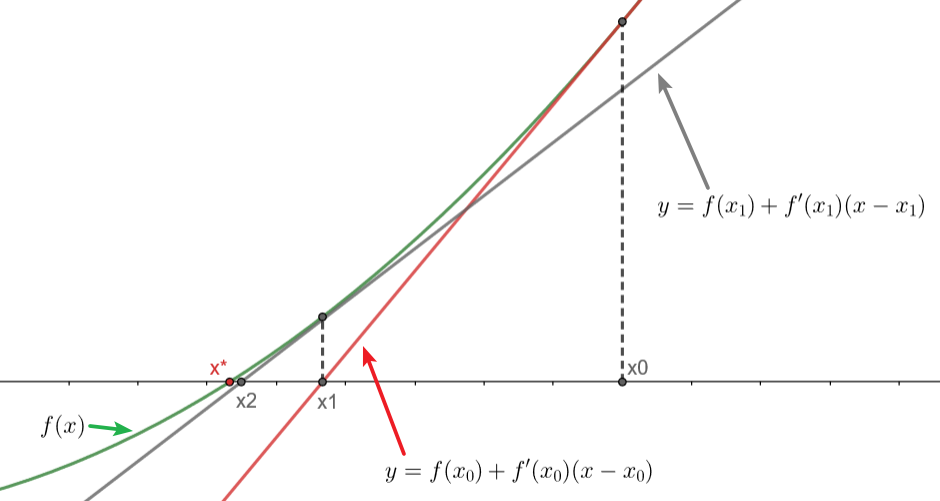
在什么情况下，牛顿法能够收敛是我们关心的问题。因此下面将介绍全局收敛定理，只要满足该定理，使用牛顿法就能够唯一收敛到方程的根。

全局收敛定理 设\(f(x)\in C^2[a,b]\)

1. \(f(a)f(b)<0\)
2. 在整个\([a,b]\)上\(f'(x)\ne0\)
3. \(f''(x)\)在\([a,b]\)上不变号
4. 选取初始值\(x_0\in[a,b]\)使得\(f''(x_0)f(x_0)>0\)

只要满足上述四个条件，就可以保证由牛顿法产生的序列\(\{x_k\}\)能够单调收敛到\(f(x)=0\)的唯一根。

1. 条件1实际上就是介值定理，保证方程有根。

2. 条件2保证函数的单调性不变，即方程只有唯一的根。

3. 条件3保证函数的凹凸性不变。

4. 条件4指导我们如何选取一个合适的初始值，使得迭代过程更够单调且收敛。

实际上在满足条件1的前提下，根据条件2，3我们可以将情况分成单调增凸函数、单调减凸函数、单调增凹函数、单调减凹函数。画一个示意图，很容易就可以理解条件4为什么这样取值。

牛顿迭代也可以看成是一种不动点迭代，迭代函数为

\[\varphi(x)=x-\frac{f(x)}{f'(x)} \]

于是我们可以得到

\[\varphi'(x)=\frac{f''(x)f(x)}{[f'(x)]^2} \]

假设方程\(f(x)=0\)的根为\(x^*\)，那么\(f(x^*)=0\)。于是，\(\varphi'(x^*)=0\)。根据函数的连续性，一定存在一个关于\(x^*\)的邻域\(|x-x^*|<\delta\)使得\(|\varphi'(x)|<1\)恒成立。

接下来只需说明\(\varphi(x)\)在区间\([x^*-\delta,x^*+\delta]\)上满足\(\varphi(x)\in[x^*-\delta,x^*+\delta]\)，也就是说\(\varphi(x)\)是一个压缩映射函数，所以牛顿迭代法当选定好合适的区间后一定是单调收敛的。

在区间\([x^*-\delta,x^*+\delta]\)上应用拉格朗日中值定理有：

\[|\varphi(x)-x^*|=|\varphi(x)-\varphi(x^*)|=|\varphi'(\xi)||x-x^*|<|x-x^*|\lt\delta \]

于是我们得到：\(\varphi(x)\in[x^*-\delta,x^*+\delta]\)。

牛顿下山法

下山法是为了防止初始值\(x_0\)选取不当造成迭代发散或无限循环的情况，在迭代过程中加入函数绝对值单调减下的约束，即\(|f(x_{k+1})|<|f(x_k)|\)。为了达到这个目的，我们将使用原始牛顿迭代法的计算结果和前一步的近似值进行加权平均：

\[x_{k+1}=\lambda\left(x_k-\frac{f(x_k)}{f'(x_k)}\right)+(1-\lambda)x_k=x_k-\lambda\frac{f(x_k)}{f'(x_k)} \]

通常，在每一步迭代中，依次取

\[\lambda=1,\frac{1}{2},\frac14,\cdots \]

不断尝试计算\(x_{k+1}\)的值，直到满足条件\(|f(x_{k+1})|<|f(x_k)|\)后，进入下一次迭代。

割线法

如果所求的问题求导很不方便，则可以利用通过\(x_k\)点处的割线来替代切线，即

\[f'(x_k)\approx\frac{f(x_k)-f(x_{k-1})}{x_k-x_{k-1}} \]

于是迭代公式变为

\[x_{k+1}=x_k-\frac{f(x_k)}{f(x_k)-f'(x_{k-1})}(x_k-x_{k-1}) \]

因此如果使用割线法，就需要两个初始值。

大M法

如果想更加偷懒一点，就可以使用某一个给定的数\(M\)来替代\(f'(x_k)\)，得到迭代公式

\[x_{k+1}=x_k-\frac{f(x_k)}{M} \]

这种做法更加简便。

3.5 收敛阶和加速收敛

同样是收敛的方法，收敛的快慢可能是不同的，我们很自然会想要去选择收敛速度足够快的方法，在这一部分将介绍收敛阶，收敛阶是衡量迭代法收敛快慢的重要指标。

3.5.1 收敛阶的定义

定义 设序列\(\{x_k\}\)收敛于\(x^*\)且\(x_k\ne x^*\)，如果存在常数\(\alpha\ge1,\lambda>0\)，使得迭代误差\(e_k=x_k-x^*\)满足极限式：

\[\lim_{k\rightarrow\infty}\frac{|e_{k+1}|}{|e_k^\alpha|}= \lim_{k\rightarrow\infty}\frac{|x_{k+1}-x^*|}{|x_k-x^*|^\alpha}=\lambda \]

则称序列\(\{x_k\}\)是\(\alpha\)阶收敛的，\(\lambda\)称为渐进误差常数。特殊地，

• 当\(\alpha=1,\lambda<1\)，称此时是线性收敛的。若\(\lambda\ge1\)，则称为次线性收敛。
• 当\(1<\alpha<2\)时，称为超线性收敛。
• 当\(\alpha=2\)时，称为平方收敛。

此外，如果将上述极限式换成下面的不等式，且当\(k\ge K\)（\(K\)为某一常数）时，下面不等式恒成立

\[|x_{k+1}-x^*|\le\lambda|x_k-x^*|^\alpha \]

则称序列\(\{x_k\}\)至少\(\alpha\)阶收敛。

若满足\(\alpha\ge1\)，都有

\[\lim_{k\rightarrow\infty}\frac{|x_{k+1}-x^*|}{|x_k-x^*|^\alpha}=0 \]

则称序列\(\{x_k\}\)超\(\alpha\)阶收敛。

3.5.2 不动点迭代的收敛阶

定理 设\(x^*\)是\(g(x)\)的不动点，如果在\(x^*\)的一个邻域内\(g(x)\)具有\(m\)阶连续导数，并且满足

\[g'(x^*)=g^{(2)}(x^*)=\cdots=g^{(m-1)}(x^*)=0,g^{(m)}(x^*)\ne0 \]

则迭代过程\(x_{k+1}=g(x_k)\)在\(x^*\)的邻域内是\(m\)阶收敛的。

证明：在点\(x^*\)处进行泰勒展开

\[g(x)=g(x^*)+g'(x^*)(x-x^*)+\cdots+\frac{g^{(m)}(\xi)}{m!}(x-x^*)^m \]

其中\(\xi\)是\(x\)和\(x^*\)之间的某个数。

于是，我们可以得到

\[x_{k+1}=g(x_k)=x^*+\frac{g^{(m)}(\xi)}{m!}(x_k-x^*)^m \]

整理一下，便可以得到

\[\lim_{k\rightarrow\infty}\frac{|x_{k+1}-x^*|}{|x_k-x^*|^m}= \lim_{k\rightarrow\infty}\left|\frac{g^{(m)}(\xi)}{m!}\right|= \left|\frac{g^{(m)}(x^*)}{m!}\right| \]

通过上述定理知道，如果在\(m=1\)的情况下，\(g'(x^*)\ne0\)那么该不动点迭代是1阶收敛的。如果\(0<|g'(x^*)|<1\)，则是线性收敛。

3.5.3 牛顿法的收敛阶

牛顿法的收敛阶

假设\(f(x)\)具有唯一零点\(x^*\)且具有二阶连续导数，为了研究牛顿法的收敛阶，在\(x_k\)处进行泰勒展开

\[f(x)=f(x_k)+f'(x_k)(x-x_k)+\frac{f''(\xi)}{2}(x-x_k)^2 \]

于是，我们有

\[0=f(x^*)=f(x_k)+f'(x_k)(x^*-x_k)+\frac{f''(\xi)}{2}(x^*-x_k)^2 \]

整理可得

\[x_k-\frac{f(x_k)}{f'(x_k)}-x^*=\frac{f''(\xi)}{2}(x^*-x_k)^2 \]

于是

\[\lim_{k\rightarrow\infty}\frac{|x_{k+1}-x^*|}{|x_k-x^*|^2}= \lim_{k\rightarrow\infty}\left|\frac{f^{''}(\xi)}{2}\right|= \left|\frac{f^{''}(x^*)}{2}\right| \]

因此，牛顿迭代法是平方收敛的。

重根的情况

但是如果方程\(f(x)\)具有\(m(\ge2)\)重根\(x^*\)，那么牛顿法的收敛将会是线性的，原因如下：

假设\(f(x)=(x-x^*)^mg(x),g(x^*)\ne0\)，那么根据牛顿迭代法有

\[\begin{aligned} x_{k+1}&=x_k-\frac{(x_k-x^*)^mg(x_k)}{m(x_k-x^*)^{m-1}g(x_k)+(x_k-x^*)^mg'(x_k)}\\ &=x_k-\frac{(x_k-x^*)g(x_k)}{mg(x_k)+(x_k-x^*)g'(x_k)} \end{aligned} \]

于是

\[\begin{aligned} x_{k+1}-x^*&=(x_k-x^*)-\frac{(x_k-x^*)g(x_k)}{mg(x_k)+(x_k-x^*)g'(x_k)}\\ &=(x_k-x^*)\frac{(m-1)g(x_k)+(x_k-x^*)g'(x_k)}{mg(x_k)+(x_k-x^*)g'(x_k)} \end{aligned} \]

因此

\[\lim_{k\rightarrow\infty}\frac{|x_{k+1}-x^*|}{|x_k-x^*|}= \lim_{k\rightarrow\infty}\left|\frac{(m-1)g(x_k)+(x_k-x^*)g'(x_k)}{mg(x_k)+(x_k-x^*)g'(x_k)}\right|=\frac{m-1}{m}<1 \]

出现重根时的加速收敛

如果我们已知根的重数\(m\)，那么我们可以将牛顿迭代格式更改为

\[x_{k+1}=x_k-m\frac{f(x_k)}{f'(x_k)} \]

根据之前的分析，我们可以得到

\[\begin{aligned} x_{k+1}-x^*&=(x_k-x^*)-\frac{(x_k-x^*)mg(x_k)}{mg(x_k)+(x_k-x^*)g'(x_k)}\\ &=(x_k-x^*)^2\frac{g'(x_k)}{mg(x_k)+(x_k-x^*)g'(x_k)} \end{aligned} \]

因此

\[\lim_{k\rightarrow\infty}\frac{|x_{k+1}-x^*|}{|x_k-x^*|^2}= \left|\frac{g'(x^*)}{mg(x^*)}\right| \]

此时，改进后的迭代格式仍然是平方收敛的。