点分治

点分治，是在树上统计答案的一种算法。它将树按照重心进行处理。

假设有一条链，如果从 \(1\) 作为根，需要 \(O(n)\) 的时间复杂度，但是我们如果递归找到重心，只需要 \(\log{n}\) 的复杂度，也就是说会把 \(O(n^2)\) 变成 \(O(nlogn)\) 的复杂度。

有时候我们需要在点分治上加入树状数组或者线段树等数据结构进行解题，复杂度变为 \(O(nlog^2n)\)

\(O(n)\) 寻找重心

inline void getroot(int now,int fa){

    siz[now]=1,mx[now]=0;

    for(register int i=head[now];i;i=nxt[i]){

        int y=to[i];

        if(vis[y]||y==fa) continue;

        getroot(y,now);

        siz[now]+=siz[y];

        mx[now]=max(mx[now],siz[y]);

    }

    mx[now]=max(mx[now],sn-siz[now]);

    if(mx[now]<mx[root]){

        root=now;

    }

}

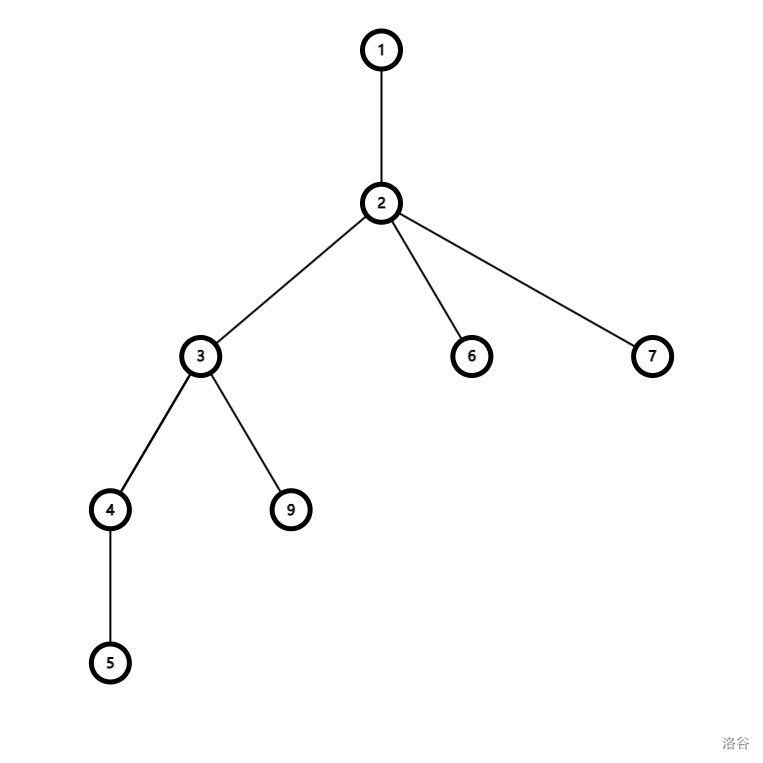
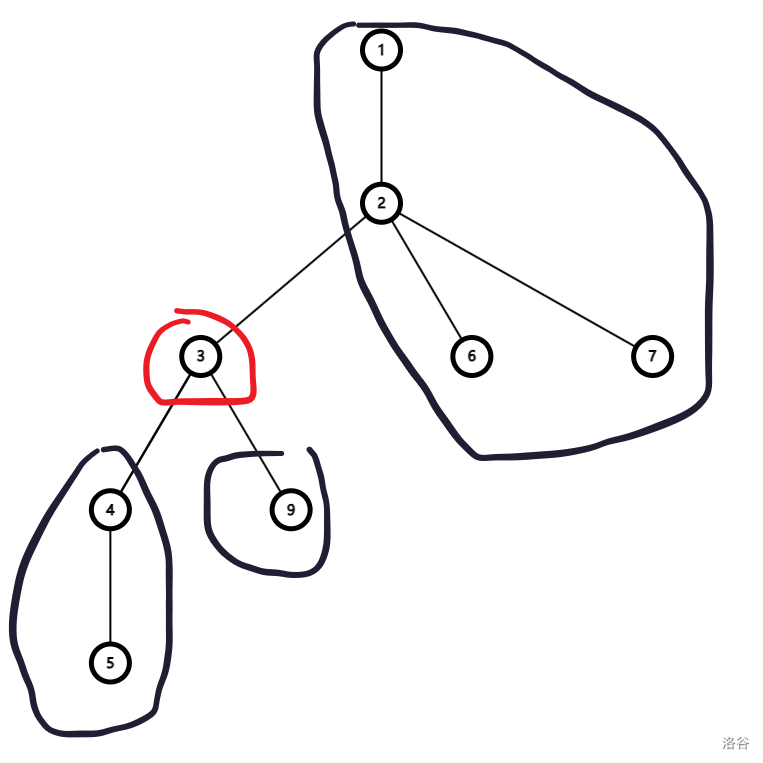
红色点是当前点，我们比较所有黑圈（子树）部分大小，使没处理的节点中最大子树中的值最小的节点即为重心。

分治

根据题意不同，我们需要设计不同的 \(getdis\) 和 \(calc\) 。

假设我们要求树上路径所有距离为 \(k\)的点对有多少个，边权都为 \(1\) 。

传送门

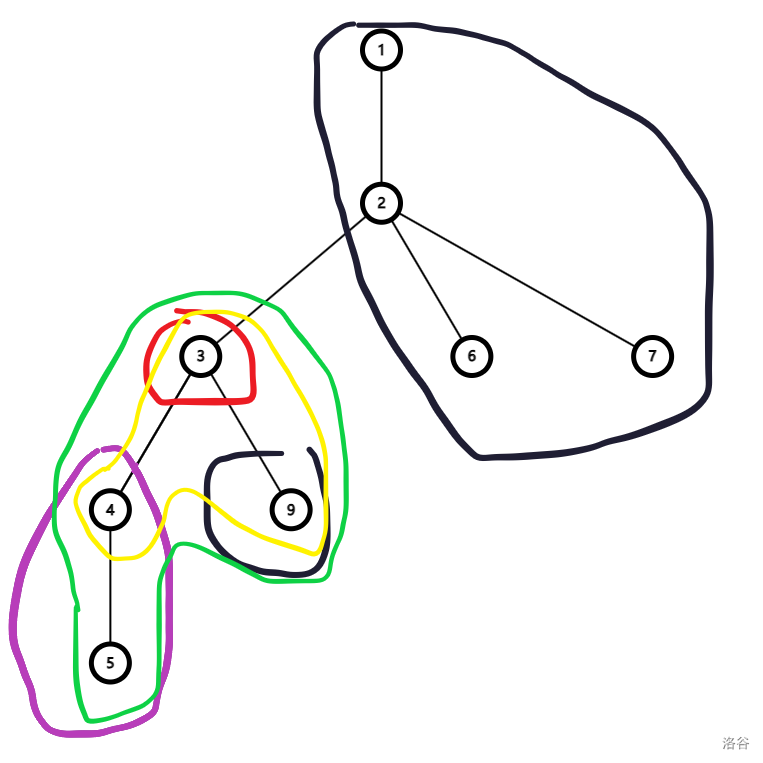
我们处理出当前子树到重心的距离，再和原来所有子树里一一累加，先加上只在当前子树的距离为 \(k\) 的点（即路径的一端是重心），再将现在距离为 \(x(1 \le x<k)\) 的点和之前所有子树的距离为 \(k-x\) 的点相乘再累加起来。

#include<bits/stdc++.h>
#define int long long
using namespace std;
namespace Testify{
    inline int read(){
        int f(1),x(0);
        char ch=getchar();
        for(;!isdigit(ch);ch=getchar()) if(ch=='-') f=-1;
        for(;isdigit(ch);ch=getchar()) x=(x<<1)+(x<<3)+(ch^48);
        return f*x;
    }
    inline void Write(int x){
        if(x>9) Write(x/10);
        putchar(x%10+48);
    }
    inline void write(int x){
        if(x<0) putchar('-'),x=-x;
        Write(x);
        putchar('\n');
    }
}
using namespace Testify;
int n,k;
const int N=50005;
int head[N],nxt[N<<1],to[N<<1],val[N<<1],tot(0);
inline void add(int x,int y){
    to[++tot]=y,nxt[tot]=head[x],head[x]=tot;
}
int SATELLITE(0);
int root,sum;
bool vis[N];
int siz[N],maxn[N];
inline void getroot(int now,int fa){
    siz[now]=1;
    for(register int i=head[now];i;i=nxt[i]){
        int y=to[i];
        if(y==fa||vis[y]) continue;
        getroot(y,now);
        siz[now]+=siz[y];
        maxn[now]=max(maxn[now],siz[y]);
    }
    maxn[now]=max(maxn[now],sum-siz[now]);
    if(maxn[now]<maxn[root]){
        root=now;
    }
}
int beyond[N],past[N];
int tong[N],cnt;
inline void getdis(int now,int fa,int dis){
    if(dis>k) return;
    if(!beyond[dis]){
        tong[++cnt]=dis;
    }
        beyond[dis]++;
    for(register int i=head[now];i;i=nxt[i]){
        int y=to[i];
        if(y==fa||vis[y]) continue;
        getdis(y,now,dis+1);
    }
}
inline void calc(int now){
    for(register int i=head[now];i;i=nxt[i]){
        int y=to[i];
        if(vis[y]) continue;
        cnt=0;
        getdis(y,now,1);
        SATELLITE+=beyond[k];
        for(register int i=1;i<=cnt;i++){
            SATELLITE+=(beyond[tong[i]]*past[k-tong[i]]);
        }
        for(register int i=1;i<=cnt;i++){
            past[tong[i]]+=beyond[tong[i]];
            beyond[tong[i]]=0;
        }
    }
    for(register int i=1;i<=k;i++){
        past[i]=0;
    }
}
inline void solve(int now){
    vis[now]=true;
    calc(now);
    for(register int i=head[now];i;i=nxt[i]){
        int y=to[i];
        if(vis[y]) continue;
        maxn[root=0]=LONG_LONG_MAX;
        sum=siz[y];
        getroot(y,0);
        solve(root);
    }
}
signed main(void){
    n=read(),k=read();
    for(register int i=1;i<n;i++){
        register int asd=read(),jkl=read();
        add(asd,jkl),add(jkl,asd);
    }
    maxn[root=0]=LONG_LONG_MAX;
    sum=n;
    getroot(1,0);
    solve(root);
    write(SATELLITE);
    return 0;
}

不知道这个代码为什么 \(TLE\) 了，但是思路就是这样的。

我们再来看看这个题的升级版

给你一棵TREE,以及这棵树上边的距离.问有多少对点它们两者间的距离小于等于K

传送门

这个题就是上面的思路，但是有树状数组统计所有 \(1\) 到 \(k\) 的数有多少个。

先统计重心为一端的，另一端在当前子树的所有符合条件的点，在统计跨过重心的路径数量。

如果当前节点到重心距离为 \(x\) 则乘上存之前的树状数组的 \(1\) 到 \(k-x\) 的 所有节点再累加到 \(ans\) 里。

树状数组用来单点修改区间查询。

#include<bits/stdc++.h>
#define int long long
using namespace std;
namespace Testify{
    inline int read(){
        int f(1),x(0);
        char ch=getchar();
        for(;!isdigit(ch);ch=getchar()) if(ch=='-') f=-1;
        for(;isdigit(ch);ch=getchar()) x=(x<<1)+(x<<3)+(ch^48);
        return f*x;
    }
    inline void Write(int x){
        if(x>9) Write(x/10);
        putchar(x%10+48);
    }
    inline void write(int x){
        if(x<0) putchar('-'),x=-x;
        Write(x);
        putchar('\n');
    }
}
using namespace Testify;
int n,k;
int SATELLITE(0);
const int N=50005;
int beyond[N];
int t[N];
#define lowbit(x) (x&(-x))
inline void update(int pos,int v){
    while(pos<=k){
        t[pos]+=v;
        pos+=lowbit(pos);
    }
}
inline int ask(int pos){
    int res=0;
    while(pos){
        res+=t[pos];
        pos-=lowbit(pos);
    }
    return res;
}
int head[N],nxt[N<<1],to[N<<1],val[N<<1],tot(0);
inline void add(int x,int y,int v){
    to[++tot]=y,nxt[tot]=head[x],head[x]=tot;
    val[tot]=v;
}
bool vis[N];
int siz[N],maxn[N],sum,root;
inline void getroot(int now,int fa){
    siz[now]=1;
    maxn[now]=0;
    for(register int i=head[now];i;i=nxt[i]){
        int y=to[i];
        if(y==fa||vis[y]) continue;
        getroot(y,now);
        siz[now]+=siz[y];
        maxn[now]=max(maxn[now],siz[y]);
    }
    maxn[now]=max(maxn[now],sum-siz[now]);
    if(maxn[now]<maxn[root]){
        root=now;
    }
}
int Sum=0;
int cnt;
int tong[N];
inline void getdis(int now,int fa,int dis){
    if(dis>k) return ;
    if(!beyond[dis]){
        tong[++cnt]=dis;
    }
    beyond[dis]++;
    Sum++;
    for(register int i=head[now];i;i=nxt[i]){
        int y=to[i];
        if(y==fa||vis[y]) continue;
        getdis(y,now,dis+val[i]);
    }
}
inline void calc(int now){

    for(register int i=head[now];i;i=nxt[i]){
        int y=to[i];
        if(vis[y]) continue;
        Sum=0;
        cnt=0;
        getdis(y,now,val[i]);
        SATELLITE+=Sum;
        // t[0]=1;
        for(register int i=1;i<=cnt;i++){
            SATELLITE+=beyond[tong[i]]*ask(k-tong[i]);
        }
        for(register int i=1;i<=cnt;i++){
            update(tong[i],beyond[tong[i]]);
            beyond[tong[i]]=0;
        }
    }
    for(register int i=1;i<=k;i++){
        t[i]=0;
    }
}
inline void solve(int now){
    vis[now]=true;
    calc(now);
    for(register int i=head[now];i;i=nxt[i]){
        int y=to[i];
        if(vis[y]) continue;
        maxn[root=0]=LONG_LONG_MAX;
        sum=siz[y];
        getroot(y,0);
        solve(root);
    }
}
signed main(void){
    n=read();
    for(register int i=1;i<n;i++){
        register int asd=read(),jkl=read(),fgh=read();
        add(asd,jkl,fgh),add(jkl,asd,fgh);
    } 
    k=read();
    sum=n;
    maxn[root=0]=LONG_LONG_MAX;
    solve(1);
    write(SATELLITE);
    return 0;
}

Race

给一棵树,每条边有权.求一条简单路径,权值和等于 \(K\) ,且边的数量最小.

\(N <= 200000, K <= 1000000\)

直接淀粉质模板套个 \(pair\) 顺便统计一下边数即可。 \(first\) 为距离，\(second\) 为边数。

#include<bits/stdc++.h>
#define int long long
using namespace std;
namespace Testify{
    inline int read(){
        int f(1),x(0);
        char ch=getchar();
        for(;!isdigit(ch);ch=getchar()) if(ch=='-') f=-1;
        for(;isdigit(ch);ch=getchar()) x=(x<<1)+(x<<3)+(ch^48);
        return f*x;
    }
    inline void Write(int x){
        if(x>9) Write(x/10);
        putchar(x%10+48);
    }
    inline void write(int x){
        if(x<0) putchar('-'),x=-x;
        Write(x);
        putchar('\n');
    }
}
using namespace Testify;
int n,k;
const int N=2e5+5;
int head[N],nxt[N<<1],to[N<<1],val[N<<1],tot(0);
inline void add(int x,int y,int w){
    to[++tot]=y,nxt[tot]=head[x],head[x]=tot;
    val[tot]=w;
}
int SATELLITE(LONG_LONG_MAX);
int root,sum;
bool vis[N];
int siz[N],maxn[N];
inline void getroot(int now,int fa){
    siz[now]=1;
    maxn[now]=0;
    for(register int i=head[now];i;i=nxt[i]){
        int y=to[i];
        if(y==fa||vis[y]) continue;
        getroot(y,now);
        siz[now]+=siz[y];
        maxn[now]=max(maxn[now],siz[y]);
    }
    maxn[now]=max(maxn[now],sum-siz[now]);
    if(maxn[now]<maxn[root]){
        root=now;
    }
}
int past[N],cnt;
typedef pair<int,int> P;
P beyond[N];
inline void getdis(int now,int fa,int dis,int c){
    if(dis>k) return;
    beyond[++cnt]=make_pair(dis,c);
    for(register int i=head[now];i;i=nxt[i]){
        int y=to[i],w=val[i];
        if(y==fa||vis[y]) continue;
        getdis(y,now,dis+w,c+1);
    }
}
pair<bool,int> judge[(int)2e6+5];
// map<int,P> judge;
int CNT(0),bin[10000000];
int sssss=0;
inline void calc(int now){
    CNT=0;
    // judge[0].second=0;
    for(register int i=head[now];i;i=nxt[i]){
        int y=to[i];
        if(vis[y]) continue;
        cnt=0;
        getdis(y,now,val[i],1);
        judge[0].first=1;
        judge[0].second=0;
        for(register int i=1;i<=cnt;i++){
            // cerr<<"asdasdassd"<<endl;
            if(judge[k-beyond[i].first].first){
                // cerr<<"asdasdassd"<<endl;
                // cerr<<beyond[i].second<<"   "<<judge[k-beyond[i].first].second<<endl;
                SATELLITE=min(SATELLITE,beyond[i].second+judge[k-beyond[i].first].second);
            }
        }
        
        for(register int i=1;i<=cnt;i++){ 
            // cerr<<"asdasdassd"<<endl;
            bin[++CNT]=beyond[i].first;
            judge[beyond[i].first].first=1;
            judge[beyond[i].first].second=min(judge[beyond[i].first].second,beyond[i].second);
        }
        
    }
    for(register int i=1;i<=CNT;i++){
        judge[bin[i]].first=0;
        judge[bin[i]].second=LONG_LONG_MAX;
    }
}
inline void solve(int now){
    vis[now]=true; 
    
    calc(now);
    for(register int i=head[now];i;i=nxt[i]){
        int y=to[i];
        if(vis[y]) continue;
        maxn[root=0]=LONG_LONG_MAX;
        sum=siz[y];
        getroot(y,0);
        solve(root);
    }
}
signed main(void){
    // freopen("dasdasd.in","r",stdin);
    n=read(),k=read();
    for(register int i=1;i<n;i++){
        register int asd=read()+1,jkl=read()+1,v=read();
        // sssss+=(asd+jkl);
        add(asd,jkl,v),add(jkl,asd,v);
    }
    maxn[root=0]=LONG_LONG_MAX;
    sum=n;
    getroot(1,0);
    for(register int i=0;i<=(int)2e6;i++){
        judge[i].first=0;
        judge[i].second=LONG_LONG_MAX;
    }
    solve(root);
    if(SATELLITE==LONG_LONG_MAX){
        puts("-1");
    }
    else{
        write(SATELLITE);
    }
    return 0;
}

采药人的路径

采药人的药田是一个树状结构，每条路径上都种植着同种药材。
采药人以自己对药材独到的见解，对每种药材进行了分类。大致分为两类，一种是阴性的，一种是阳性的。
采药人每天都要进行采药活动。他选择的路径是很有讲究的，他认为阴阳平衡是很重要的，所以他走的一定是两种药材数目相等的路径。采药工作是很辛苦的，所以他希望他选出的路径中有一个可以作为休息站的节点（不包括起点和终点），满足起点到休息站和休息站到终点的路径也是阴阳平衡的。他想知道他一共可以选择多少种不同的路径。

当一端到重心距离和为0，且之前没有休息点，另一端到重心距离和为0，且之前没有休息点时，重心作为休息点，这是合法的。

其他就是一端有休息点的情况，但是重心一端距离为 \(x\) 的话，另一端必须为 \(-x\) 。分别统计一下即可。

#include<bits/stdc++.h>
#define int long long
using namespace std;
namespace Testify{
    inline int read(){
        int f(1),x(0);
        char ch=getchar();
        for(;!isdigit(ch);ch=getchar()) if(ch=='-') f=-1;
        for(;isdigit(ch);ch=getchar()) x=(x<<1)+(x<<3)+(ch^48);
        return f*x;
    }
    inline void Write(int x){
        if(x>9) Write(x/10);
        putchar(x%10+48);
    }
    inline void write(int x){
        if(x<0) putchar('-'),x=-x;
        Write(x);
        putchar('\n');
    }
}
using namespace Testify;
int n,m,SATELLITE;
const int N=2e5+5;
int head[N],nxt[N<<1],to[N<<1],tot(0),val[N<<1];
inline void add(int x,int y,int w){
    to[++tot]=y,nxt[tot]=head[x],head[x]=tot;
    val[tot]=w;
}
int siz[N],maxn[N],root,sum;
bool vis[N];
inline void getroot(int now,int fa){
    siz[now]=1;
    maxn[now]=0;
    for(register int i=head[now];i;i=nxt[i]){
        int y=to[i];
        if(y==fa||vis[y]) continue;
        getroot(y,now);
        siz[now]+=siz[y];
        maxn[now]=max(maxn[now],siz[y]);
    }
    maxn[now]=max(maxn[now],sum-siz[now]);
    if(maxn[now]<maxn[root]){
        root=now;
    }
}
#define _ +n
int f[N<<1][2],g[N<<1][2];
int cnt[10000000];
int dep=0;
inline void getdis(int now,int fa,int dis,int Dep){
    dep=max(dep,Dep);
    if(cnt[dis _]){
        f[dis _][1]++;
    }
    else{
        f[dis _][0]++;
    }
    cnt[dis _]++;
    for(register int i=head[now];i;i=nxt[i]){
        int y=to[i];
        if(y==fa||vis[y]) continue;
        getdis(y,now,dis+val[i],Dep+1);
    }
    cnt[dis _]--;
}
inline void calc(int now){
    int Max=-1;
    for(register int i=head[now];i;i=nxt[i]){
        int y=to[i];
        if(vis[y]) continue;
        dep=-1;
        getdis(y,now,val[i],1);
        Max=max(Max,dep);
        SATELLITE+=f[0 _][0]*g[0 _][0];
        SATELLITE+=(f[0 _][1]);
        for(register int j=-Max;j<=Max;j++){
            // if(j==0){
            //     SATELLITE+=(f[j _][1]);
            // }
                SATELLITE+=(f[j _][1]*g[-j _][0]);

                SATELLITE+=(f[j _][1]*g[-j _][1]);
                SATELLITE+=(f[j _][0]*g[-j _][1]);
        }
        for(register int j=-Max;j<=Max;j++){
            g[j _][0]+=f[j _][0];
            g[j _][1]+=f[j _][1];
            f[j _][0]=f[j _][1]=0;
        }
    }
    for(register int i=-Max;i<=Max;i++){
        g[i _][0]=g[i _][1]=0;
    }
}
inline void solve(int now){
    vis[now]=true;
    calc(now);
    for(register int i=head[now];i;i=nxt[i]){
        int y=to[i];
        if(vis[y]) continue;
        sum=siz[y];
        maxn[root=0]=LONG_LONG_MAX;
        getroot(y,0);
        solve(root);
    }
}
signed main(void){
    n=read();
    for(register int i=1;i<n;i++){
        register int asd=read(),jkl=read(),fgh=read();
        if(!fgh) fgh=-1;
        add(asd,jkl,fgh),add(jkl,asd,fgh);
    }
    maxn[root=0]=LONG_LONG_MAX;
    sum=n;
    getroot(1,0);
    solve(root);
    write(SATELLITE); 
    return 0;
}

树的难题

给你一棵 \(n\) 个点的无根树。

树上的每条边具有颜色。一共有 \(m\) 种颜色，编号为 \(1\) 到 \(m\)，第 \(i\) 种颜色的权值为 \(c_i\)。

对于一条树上的简单路径，路径上经过的所有边按顺序组成一个颜色序列，序列可以划分成若干个相同颜色段。定义路径权值为颜色序列上每个同颜色段的颜色权值之和。

请你计算，经过边数在 \(l\) 到 \(r\) 之间的所有简单路径中，路径权值的最大值。

开两个权值线段树，一个维护当前颜色为 \(C\) ，一个维护不为 \(C\) 的从重心向子树的第一条边的颜色大小的最大值。

先按照颜色排序，使得颜色相同的在一起，便于处理。

在 \(getdis\) 的时候统计答案。之后再更新相同颜色的这棵树。

如果现在路径和之前颜色相同，就是 \(x+y-color[nowcol]\) ，否则就是 \(x+y\) 。

再把颜色相同的树加到颜色不同的树中。

#include<bits/stdc++.h>
using namespace std;
#define int long long
namespace Testify{
    inline int read(){
        int f(1),x(0);
        char ch=getchar();
        for(;!isdigit(ch);ch=getchar()) if(ch=='-') f=-1;
        for(;isdigit(ch);ch=getchar()) x=(x<<1)+(x<<3)+(ch^48);
        return f*x;
    }
    inline void Write(int x){
        if(x>9) Write(x/10);
        putchar(x%10+48);
    }
    inline void write(int x){
        if(x<0) putchar('-'),x=-x;
        Write(x);
        putchar('\n');
    }
}

using namespace Testify;
const int N=2e5+5;
int n,m,L,R;
int color[N];
// tojita seikai
typedef pair<int,int> P;
vector<P> e[N];
int Root,maxn[N],siz[N],sum;
bool vis[N];
inline bool cmp(P a,P b){
    return a.second<b.second;
}
inline void findroot(int now,int fa){
    siz[now]=1;
    maxn[now]=0;
    for(P op:e[now]){
        int y=op.first;
        if(y==fa||vis[y]) continue;
        findroot(y,now);
        siz[now]+=siz[y];
        maxn[now]=max(maxn[now],siz[y]);
    }
    maxn[now]=max(maxn[now],sum-siz[now]);
    if(maxn[now]<maxn[Root]){
        Root=now;
    }
}
struct segmenttree{
    #define lid root<<1
    #define rid root<<1|1
    struct node{
        int Max,lazy;
    }t[N<<3];
    inline void clear(){
        t[1].lazy=1;
        t[1].Max=-2e9;
    }
    inline void pushdown(int root){
        if(t[root].lazy){
            t[lid].lazy=t[rid].lazy=1;
            t[lid].Max=t[rid].Max=-2e9;
            t[root].lazy=0;
        }
    }
    inline void pushup(int root){
        t[root].Max=max(t[lid].Max,t[rid].Max);
    }
    inline void change(int root,int l,int r,int pos,int val){
        if(l==r){
            t[root].lazy=0;
            t[root].Max=max(t[root].Max,val);
            return ;
        }
        int mid=(l+r)>>1;
        pushdown(root);
        if(pos<=mid){
            change(lid,l,mid,pos,val);
        }
        else{
            change(rid,mid+1,r,pos,val);
        }
        pushup(root);
    }
    inline int ask(int root,int l,int r,int vl,int vr){
        if(l>vr||r<vl){
            return -2e9;
        }
        if(vl<=l&&r<=vr){
            return t[root].Max;
        }
        if(t[root].lazy) return -2e9;
        pushdown(root);
        int mid=(l+r)>>1;
            return max(ask(lid,l,mid,vl,vr),ask(rid,mid+1,r,vl,vr));
    }
}same,different;
int nowcol;
int Credit(-2e9);
inline void getdis(int now,int fa,int val,int lastcol,int dis){
    if(dis>R) return ;
    Credit=max({Credit,val+same.ask(1,0,n,max(0ll,L-dis),R-dis)-color[nowcol],val+different.ask(1,0,n,max(0ll,L-dis),R-dis)});
    for(P op:e[now]){
        int y=op.first,w=op.second;
        if(y==fa||vis[y]){
            continue;
        }
        if(w==lastcol){
            getdis(y,now,val,lastcol,dis+1);
        }
        else{
            getdis(y,now,val+color[w],w,dis+1);
        }
    }
}
inline void updatesame(int now,int fa,int val,int lastcol,int bian){
    if(bian>R){
        return;
    }
    same.change(1,0,n,bian,val);
    for(P op:e[now]){
        int y=op.first,w=op.second;
        if(y==fa||vis[y]){
            continue;
        }
        if(w==lastcol){
            updatesame(y,now,val,lastcol,bian+1);
        }
        else{
            updatesame(y,now,val+color[w],w,bian+1);
        }
    }
}
inline void updatedifferent(int now,int fa,int val,int lastcol,int bian){
    if(bian>R){
        return;
    }
    different.change(1,0,n,bian,val);
    for(P op:e[now]){
        int y=op.first,w=op.second;
        if(y==fa||vis[y]){
            continue;
        }
        if(w==lastcol){
            updatedifferent(y,now,val,lastcol,bian+1);
        }
        else{
            updatedifferent(y,now,val+color[w],w,bian+1);
        }
    }
}
int sta[N],top=0;
inline void calc(int now){
    top=0;
    different.clear();
    same.clear();
    for(register int i=0;i<e[now].size();i++){
        int y=e[now][i].first;
        if(vis[y]) continue;
        int pastcol;
        if(i==0) goto tojitaseikai;
        pastcol=e[now][i-1].second;
        if(i==0||e[now][i].second==pastcol){
            sta[++top]=y;
            continue;
        }
        nowcol=pastcol;
        for (int j=1;j<=top;j++){
			getdis(sta[j],now,color[e[now][i-1].second],e[now][i-1].second,1);
			updatesame(sta[j],now,color[e[now][i-1].second],e[now][i-1].second,1);
		}
		same.clear();
		for(int j=1;j<=top;j++){
			updatedifferent(sta[j],now,color[e[now][i-1].second],e[now][i-1].second,1);
		}
        tojitaseikai:
        sta[top=1]=e[now][i].first;
    }
    same.clear();
    nowcol=e[now][e[now].size()-1].second;
    for(register int i=1;i<=top;i++){
        getdis(sta[i],now,color[nowcol],nowcol,1);
        updatesame(sta[i],now,color[nowcol],nowcol,1);
    }
}
inline void solve(int now){
    vis[now]=true;
    calc(now);
    for(P op:e[now]){
        int y=op.first;
        if(vis[y]) continue;
        maxn[Root=0]=INT_MAX;
        sum=siz[y];
        findroot(y,now);
        solve(Root);
    }
}
signed main(void){
    n=read(),m=read(),L=read(),R=read();
    for(register int i=1;i<=m;i++){
        color[i]=read();
    }
    for(register int i=1;i<n;i++){
        int asd=read(),jkl=read(),fgh=read();
        e[asd].push_back(make_pair(jkl,fgh));
        e[jkl].push_back(make_pair(asd,fgh));
    }
    for(register int i=1;i<=n;i++){
        sort(e[i].begin(),e[i].end(),cmp);
    }
    maxn[Root=0]=INT_MAX;
    sum=n;
    findroot(1,0);
    solve(Root);
    write(Credit);
    return 0;
}