递归分治 --- 例题1.全排列

一.问题描述

设计一个递归算法生成n个元素{r1, r2, … , rn}的全排列.
此题与力扣主站第46题 --- 全排列相同,以及力扣主站第47题 --- 全排列Ⅱ

二.解题思路

设R={r1,r2...,rn}是要进行排列的n个元素，Ri=R-{ri}.集合X中的元素的全排列记为Perm(X).(ri)Perm(X)表示在全排列X的每个排列前加上前缀ri得到的排列.

R的全排列可归纳定义为如下：

• 当n==1时，Perm(R)=(r),其中r是集合R中唯一的元素.
• 当n > 1时，Perm(R)由(r1)Perm(R1),(r2)Perm(r2),...,(rn)Perm(rn)构成

通过上述分析,我们可以很清晰地看到,规模较大的问题可以划分为规模较小的问题来,并且总问题的解可以由每个小问题的解合并而来.
有了这个性质,那么我们很自然地就可以联系上递归分治思想.

代码如下:

void Perm(T list[], int low, int high)
{
    if(low == high)		//表示已经填到最后一个字符,输出答案
    {
        for(int i=0; i<=high; ++i)
        {
            cout<<list[i];
            cout.width(4);
        }
        cout<<'\n';
    }
    for(int i=low; i<=high; ++i)  //0~low为已经填好的字符,我们在low~high中选择新字符填入,即将list[i]与list[low]交换位置
    {
        swap(list[i], list[low]);
        Perm(list, low+1, high);  //继续递归填写下一个字符,参数low变为low+1
        swap(list[i], list[low]); //递归回来之后记得交换回来,恢复原样
    }
}

下面我们更深一步,考虑一下如果有重复元素在数组中应该怎么办?

由于全排列就是从第一个数字起每个数分别与它后面的数字交换.我们先尝试加个这样的判断——如果一个数与后面的数字相同那么这二个数就不交换了.
如122，第一个数与后面交换得212、221.然后122中第二数就不用与第三个数交换了，但对212，它第二个数与第三个数是不相同的，交换之后得到221,与由122中第一个数与第三个数交换所得的221重复了.所以这个方法不行.

换种思维，对122，第一个数1与第二个数2交换得到212，然后考虑第一个数1与第三个数2交换，

此时由于第三个数等于第二个数，所以第一个数不再与第三个数交换.再考虑212，它的第二个数与第三个数交换可以得到解决221.此时全排列生成完毕.

这样我们也得到了在全排列中去掉重复的规则——去重的全排列就是从第一个数字起每个数分别与它后面非重复出现的数字交换.用编程的话描述就是第i个数与第j个数交换时，要求[i,j)中没有与第j个数相等的数.即保证每次填入的数一定是这个数所在重复数集合中「从左往右第一个未被填过的数.
判断在str数组中，[nBegin,nEnd]中是否有数字与下标为nEnd的数字相等

代码如下:

#include<bits/stdc++.h>
using namespace std;
bool IsSwap(char *str, int nBegin, int nEnd)  //保证每次填入的数一定是这个数所在重复数集合中「从左往右第一个未被填过的数字」
{
    for(int i=nBegin; i<nEnd; i++)
        if(str[i]==str[nEnd]) return false;
    return true;
}
// k表示当前选取到第几个数，m表示数组大小
void AllRange(char *str, int k, int m)
{
    if(k==m)
    {
        static int count = 1;
        string ans = "";
        for(int i=0; i<m; i++) ans += str[i];
        cout<<"第"<<count++<<"个排列是"<<ans<<endl;
    }
    else 
    {
        for(int i=k; i<m; i++)
        {
            if(IsSwap(str, k, i))  //同一层中相同的元素只有第一个有用
            {
                swap(str[i], str[k]);
                AllRange(str, k+1, m);
                swap(str[i], str[k]);
            }
        }
    }
}
int main()
{
    // cout<<"数组中没有重复元素的全排列:"<<endl;
    // int n;
    // cout<<"请输入数组大小:";
    // while(cin>>n && n!=0)
    // {
    //     cout<<"请输入数组元素:"<<endl;
    //     int *a = new int[n];
    //     for(int i=0; i<n; i++) cin>>a[i];
    //     Perm(a, 0, n);
    //     cout<<"请输入数组大小:";
    // }

    cout<<"数组中有重复元素的全排列:"<<endl;
    int n;
    cout<<"请输入数组大小:";
    while(cin>>n && n!=0)
    {
        cout<<"请输入数组元素:"<<endl;
        char *a = new char[n];
        for(int i=0; i<n; i++)  cin>>a[i];
        AllRange(a, 0, n);
        cout<<"请输入数组大小:";
    }
    system("pause");
    return 0;
}

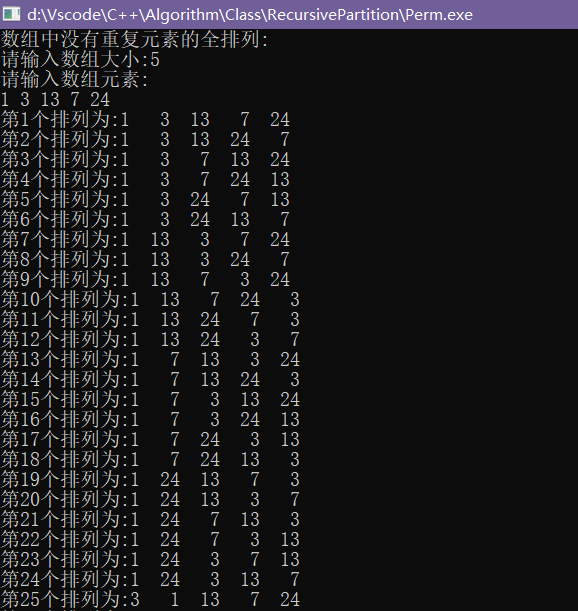
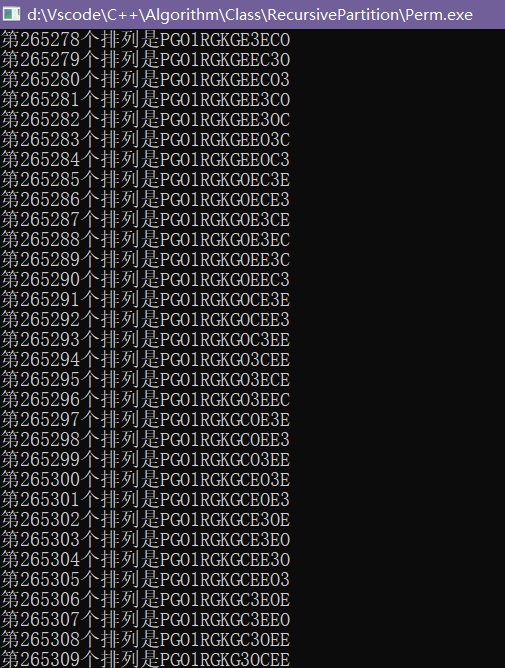
运行结果:(第一幅图为没有重复元素的全排列,第二幅图为有重复元素的全排列(数据太猛了,13个字符的全排列跑了很久))

参考毕方明老师《算法设计与分析》课件.

如果觉得本篇文章对你有所帮助,欢迎大家来到我的个人博客网站---乔治的编程小屋逛一逛吧.