动态规划 --- 例题9. 0-1背包问题

一.题目描述

背包问题：已知有n种物品和一个可容纳C重量的背包，每种物品i的重量为Wi。假定将物品i的一部分Xi放入背包就会得到Pi的效益，这里，0≤Xi≤1，Pi＞0。那么，采用怎样的装包方法才会使装入背包物品的总效益最大呢？其形式化描述为：

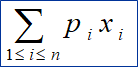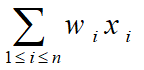Max 约束条件: <=C, 其中， 0≤x≤1, p＞0, w＞0, 1≤i≤n

满足约束条件的任一集合（x1,…,xn）是一个可行解（即能装下），使目标函数取最大值的可行解是最优解。背包问题的另一个变形就是0/1背包问题。即限定Xi的取值为0或1，其余条件不变。
普通的背包问题采用贪心法来解决。
0/1背包问题可采用动态规划法、回溯法、分支限解法来解决。
如何用动态规划法求解0/1背包问题？

二.解题思路

1.最优子结构性质(略)

2.递归计算最优值

动态规划:
一句话,所有的动态规划都是从一个网格开始的.我们在这里构造我们自己的表格.

动态规划:
// dp[i][j]表示背包容量为j时,装载前i个物品可以获得的最大价值
// 1.dp[i][j] = dp[i-1][j],  j<w[i]   						   背包没有足够容量装入物品i,所以直接等于前i-1个最大价值
// 2.dp[i][j] = max(dp[i-1][j-w[i]]+v[i], dp[i-1][j]),  j>=w[i]  记住,这里虽然我们背包能够有足够容量装入物品i,但是我们要考虑是否装入,所以需要拿装入和不装入的两个值进行比较,之后选择更大的一个

我们自底向上构造表格,最后输出最后一行最后一个即为所求的最大价值.
(如果自顶向下,那么就是递归法,由于该问题具有子问题的重叠性,所以我们会产生很多重复的计算.这一点我们在之前的文章中已经说过了.当然了,我们可以使用[备忘录法](# 备忘录法),每求得一个子问题的解我们就可以保存,之后往下递归时,先查询是否该子问题已经求结果,利用常数时间可以知道子问题的解,帮助我们节省时间.)

3.构造最优解

我们在构建表格的时候,其实已经记录了最优解的信息.只要在得到完整表格之后,往回回溯就可以.
看代码,应该很清晰.

代码如下:

// 0-1背包问题
// 动态规划:
// dp[i][j]表示背包容量为j时,装载前i个物品可以获得的最大价值
// dp[i][j] = dp[i-1][j],  j<w[i]
//          = max(dp[i-1][j-w[i]]+v[i], dp[i-1][j]),  j>=w[i]
#include<bits/stdc++.h>
using namespace std;
const int N = 100;
int dp[N][N];
void KnapSack(int n, int C, int w[], int v[])  //n表示一共n个物品,C表示背包总容量
{
    for(int i=0; i<=n; i++)  //初始化,表示零个物品,自然价值为0
        dp[i][0] = 0;
    for(int j=0; j<=C; j++)  //初始化,表示背包容量为0,自然价值为0
        dp[0][j] = 0;
    for(int i=1; i<=n; i++)
    {
        for(int j=1; j<=C; j++)
        {
            if(j<w[i-1])  //背包装不下该物品
            {
                dp[i][j] = dp[i-1][j];
            }
            else  //背包能够装下该物品,考虑到底装不装
            {
                dp[i][j] = max(dp[i-1][j-w[i-1]]+v[i-1], dp[i-1][j]);
            }
        }
    }
    int j = C;  //开始构建最优解
    int x[n];  //用来记录每个物品被选中与否
    for(int i=n; i>0; i--)
    {
        if(dp[i][j] > dp[i-1][j])
        {
            x[i-1] = 1;
            j = j-w[i-1];
        }
        else x[i-1] = 0;
    }
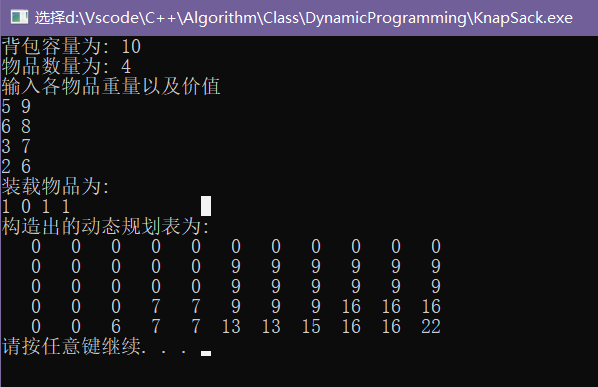
    cout<<"装载物品为:"<<endl;
    for(int i=0; i<n; i++)
    {
        cout<<x[i]<<" ";
    }
    cout<<endl<<"构造出的动态规划表为: "<<endl;
    for(int i=0; i<=n; i++)
    {
        for(int j=0; j<=C; j++)
        {
            cout.width(4);
            cout<<dp[i][j];
        }
        cout<<endl;
    }
    return ;
}
int main()
{
    int n, C;
    cout<<"背包容量为: ";
    cin>>C;
    cout<<"物品数量为: ";
    cin>>n;
    cout<<"输入各物品重量以及价值"<<endl;
    int w[n], v[n];
    for(int i=0; i<n; i++)
    {
        cin>>w[i]>>v[i];
    }
    KnapSack(n, C, w, v);
    system("pause");
    return 0;
}

运行结果:

备忘录法:

动态规划求解问题的一个基本要素：子问题的重叠性质。利用此性质，在递推工程中，对每个问题只解一次，并保存在表格中，当再次需要求解此子问题时，只要简单地用常数时间查看结果。这就是动态规划优于直接递归计算的原因。例：矩阵连乘问题
备忘录方法：是动态规划法的一种变形，它也用表格保存子问题答案，以备查看，而不必重复计算，但属于自顶向下的递归方式。备忘录方法为每个子问题建立记录项，开始存放一个特殊的初始值，表示该问题尚未求解。处理每个子问题时，先查看对应记录项，如果是初始值，则表明遇到，求解该问题并更新对应记录项。否则，说明该问题已求解过，只需要从记录项中取出该问题解答即可。

什么时候用动态规划方法？
当所有子问题都至少要解一次时，用动态规划算法。此时，动态规划方法没有任何多余计算。
什么时候用备忘录方法？
当子问题空间的部分子问题不必求解时，用备忘录方法较为有利。

如果觉得本篇文章对你有所帮助,欢迎大家来到我的个人博客网站---乔治的编程小屋逛一逛吧.