外排序&归并排序具体分析

问题：10g大小的数据，只有1g大小的内存？如何对他们进行排序？

基本思想分治加多路归并

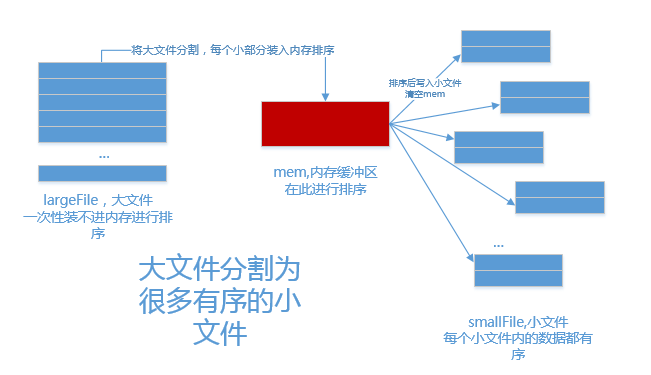
读取10g的大文件，用指针读读入0到1g的数据到内存，然后排序，然后写入到小文件

就这样写好了10个排好序的小文件

对于普通的归并排序

每次读入，10个文件里面最前面的那个数，比较9次，将最小的那个写入大文件，最小的那个数指针后移。到第二位。

总共的数字是n个的话，时间复杂度就是n*(k-1)

但在每轮比较的过程中，我们其实后一轮只是在前一轮的基础上，改变了一个数字，前一轮的一些信息我们是可以利用得到的，所以我们这里采用树选择排序的方法

胜者树和败者树：

胜者树和败者树都是完全二叉树，是树形选择排序的一种变型。每个叶子结点相当于一个选手，每个中间结点相当于一场比赛，每一层相当于一轮比赛。

不同的是，胜者树的中间结点记录的是胜者的标号；而败者树的中间结点记录的败者的标号（然后拿来比较的确实胜者，所以在根节点除了维持最终败者的节点，同时也维持了最终胜者的节点）。

胜者树与败者树可以在log(n)的时间内找到最值。任何一个叶子结点的值改变后，利用中间结点的信息，还是能够快速地找到最值。在k路归并排序中经常用到。

胜者树：

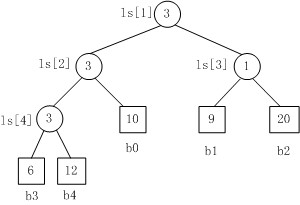
上图是一个胜者树的示例。规定数值小者胜。

1.         b3 PK b4，b3胜b4负，内部结点ls[4]的值为3；

2.         b3 PK b0，b3胜b0负，内部结点ls[2]的值为3；

3.         b1 PK b2，b1胜b2负，内部结点ls[3]的值为1；

4.         b3 PK b1，b3胜b1负，内部结点ls[1]的值为3。.

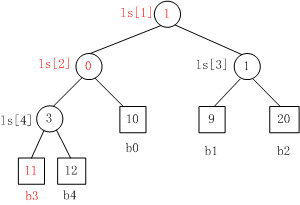
上图中叶子结点b3的值变为11时，重构的胜者树下图所示。

1.         b3 PK b4，b3胜b4负，内部结点ls[4]的值为3；

2.         b3 PK b0，b0胜b3负，内部结点ls[2]的值为0；

3.         b1 PK b2，b1胜b2负，内部结点ls[3]的值为1；

4.         b0 PK b1，b1胜b0负，内部结点ls[1]的值为1。.

 

 败者树：（除了根部多维持一个节点，再就是修改一个节点的时候，不用去与它的兄弟节点比较，直接去与它的父节点进行比较）

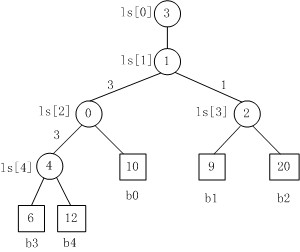
上图是一棵败者树。规定数大者败。

1.         b3 PK b4，b3胜b4负，内部结点ls[4]的值为4；

2.         b3 PK b0，b3胜b0负，内部结点ls[2]的值为0；

3.         b1 PK b2，b1胜b2负，内部结点ls[3]的值为2；

4.         b3 PK b1，b3胜b1负，内部结点ls[1]的值为1；

5.         在根结点ls[1]上又加了一个结点ls[0]=3，记录的最后的胜者。

 

败者树重构过程如下：

·            将新进入选择树的结点与其父结点进行比赛：将败者存放在父结点中；而胜者再与上一级的父结点比较。

·            比赛沿着到根结点的路径不断进行，直到ls[1]处。把败者存放在结点ls[1]中，胜者存放在ls[0]中。

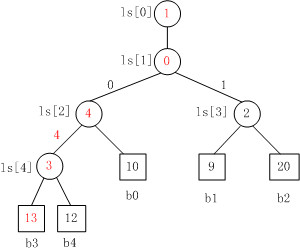
上图是当b3变为13时，败者树的重构图。

       注意，败者树的重构跟胜者树是不一样的，败者树的重构只需要与其父结点比较。对照Fig. 3来看，b3与结点ls[4]的原值比较，ls[4]中存放的原值是结点4，即b3与b4比较，b3负b4胜，则修改ls[4]的值为结点3。同理，以此类推，沿着根结点不断比赛，直至结束。 

       由上可知，败者树简化了重构。败者树的重构只是与该结点的父结点的记录有关，而胜者树的重构还与该结点的兄弟结点有关

 

在选用数选择排序以后我们的时间复杂度就变为了log(k)*(n-1)

 

在对每个小文件内排序的时候，我们也需要选定一定的内排序的方法（这个当时阿里面试官怼我了）

 

当原表有序或基本有序时，直接插入排序和冒泡排序将大大减少比较次数和移动记录的次数，时间复杂度可降至O（n）；

而快速排序则相反，当原表基本有序时，将蜕化为冒泡排序，时间复杂度提高为O（n2）；

原表是否有序，对简单选择排序、堆排序、归并排序和基数排序的时间复杂度影响不大。

所以不要干啥就快排！！！记住