拼多多提前批7.28

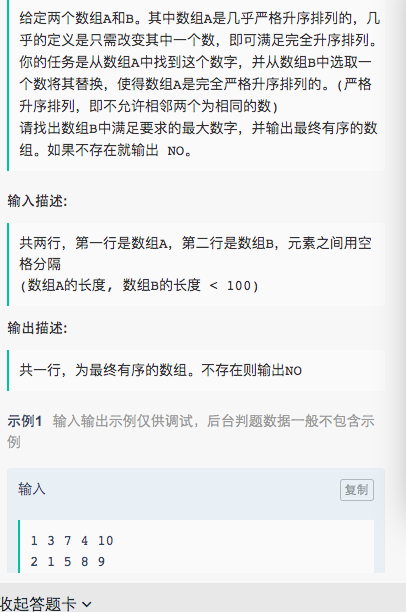
思想是拿到第一个比后面大的下标，这个下标后后一位都可能被替代

public class Main1 {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
       String a=sc.nextLine();
       String b=sc.nextLine();
       String[] aa=a.split(" ");
       String[] bb=b.split(" ");
       int[] at=new int[aa.length+2];
       Integer[] bt=new Integer[bb.length];
       for(int i=1;i<aa.length+1;i++) {
           at[i]=Integer.parseInt(aa[i-1]);
       }
       at[0]=Integer.MIN_VALUE;
       at[aa.length+1]=Integer.MAX_VALUE;
       for(int i=0;i<bb.length;i++) {
           bt[i]=Integer.parseInt(bb[i]);
       }
       Arrays.sort(bt,Collections.reverseOrder());
       Main1 m=new Main1();
       int tepm=m.get(at);
       int flag=0;
       for(int j=0;j<bb.length;j++) {
          if(bt[j]>at[tepm-1]&&bt[j]<at[tepm+1])
          {
              at[tepm]=bt[j];
              flag=1;
              break;
          }
          if(bt[j]>at[tepm]&&bt[j]<at[tepm+2])
          {
              at[tepm+1]=bt[j];
              flag=1;
              break;
          }
       }
       if(flag==1) {
           for(int i=1;i<at.length-1;i++)
           {
               System.out.print(at[i]+" ");
           }
       }
       else
       {
           System.out.print("NO");
       }
    }
    public int get(int[] a) {
        int i=0;
        for(int j=1;j<a.length+1;j++) {
            if(a[j]>=a[j+1])
            {
                i=j;
                break;
            }
        }
        return i;
    }
 }

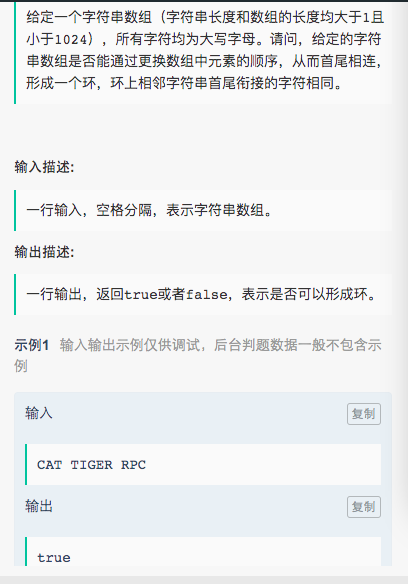
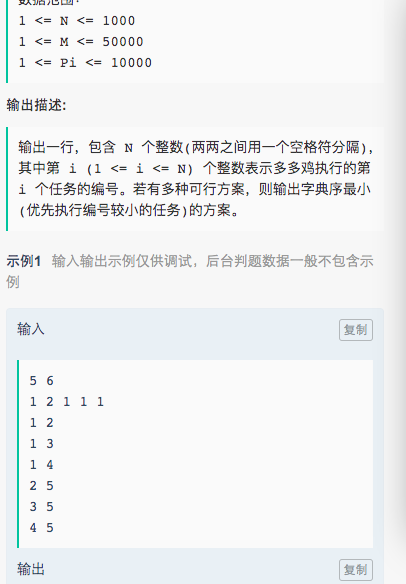
还有一个我感觉就是最长递归子序列改进版本：通过率只有50%

public class Main{
    static class rec{
        int l;
        int w;
        rec(int l,int w){
            this.l=l;
            this.w=w;
        }
    }
    public static void main(String[] args) {
          Scanner sc=new Scanner(System.in);
          int n=sc.nextInt();
          int[] l=new int[n];
          int[] w=new int[n];
          rec[] a=new rec[n];
          for(int i=0;i<n;i++) {
              l[i]=sc.nextInt();
          }
          for(int j=0;j<n;j++) {
              a[j]=new rec(l[j],sc.nextInt());      
          }
          Arrays.sort(a,(o1,o2)->{
              return o1.w==o2.w?o1.l-o2.l:o1.l-o2.l;
          });
          Main m=new Main();
          System.out.println(m.lengthOfLIS(a));
    }
    public int lengthOfLIS(rec[] nums) {
        if(nums.length==0||nums==null) return 0;
        int[] ends=new int[nums.length];
        int[] ll=new int[nums.length];
        ends[0]=nums[0].w;
        ll[0]=nums[0].l;
        int len=1;
        for(int i=1;i<nums.length;i++)
        {
            if(nums[i].w*7>=ends[len-1]&&nums[i].l>ll[len-1]) {
                ends[len]=ends[len-1]+nums[i].w;
                ll[len]=nums[i].l;
                len++;
            }
            else
            {
                int pos=BiSearch(ends,len, nums[i].w*7);
                if(pos>0){
                    if(nums[i].l>ll[pos-1])
                      ends[pos]=ends[pos-1]+nums[i].w;
                }
                  
                else
                {
                    ends[pos]=nums[i].w;
                    ll[pos]=nums[i].l;
                }
            }
            
        }
        return len;
    }
    int BiSearch(int[] b, int len, int w)  
    {  
        int left = 0, right = len - 1;  
        int mid;  
        while (left <= right)  
        {  
            mid = left + (right-left)/2;  
            if (b[mid] > w)  
                right = mid - 1;  
            else if (b[mid] < w)  
                left = mid + 1;  
            else    //找到了该元素，则直接返回  
                return mid;  
        }  
        return left;//数组b中不存在该元素，则返回该元素应该插入的位置  
    } 
}