TreeMap,TreeSet

查询的话就和普通的平衡二叉树一样。时间复杂度O(logn)

 

这里我们回顾红黑树的特点：

1.根节点为黑色

2.红色节点的子节点一定都是黑色

3.每个叶子节点都是黑色的（空节点）

4.从任一节点到其每个叶子的路径都包含相同数目的黑色节点。

红黑树和普通的平衡二插树最大的优势就是任何不平衡都可以在三次以内解决。

AVL 树是高度平衡的，频繁的插入和删除，会引起频繁的reblance，导致效率下降
红黑树不是高度平衡的，平衡因子是可能大于1的，算是一种折中，插入最多两次旋转，删除最多三次旋转

 

TreeMap特点：

1. 键值不允许重复
2. 默认会对键进行排序，所以键必须实现Comparable接口或者使用外部比较器
3. 查找、移除、添加操作的时间复杂度为log(n)
4. 底层使用的数据结构是红黑树

TreeMap实现SortedMap和NavigableMap接口（增加了排序的功能）

查询的话和普通的AVL树是一样的，主要是插入：插入以后需要调整

public V put(K key, V value) {
    ......
    int cmp;
    Entry<K,V> parent;
    if (key == null)
        throw new NullPointerException();
    Comparable<? super K> k = (Comparable<? super K>) key;//使用元素的自然顺序
    do {
        parent = t;
        cmp = k.compareTo(t.key);
        if (cmp < 0) t = t.left;//向左找
        else if (cmp > 0) t = t.right;//向右找
        else return t.setValue(value);
    } while (t != null);
    Entry<K,V> e = new Entry<>(key, value, parent);//创建并插入新的entry，最开始一定是插在叶子节点的，而且新插入的节点一定是红色
    if (cmp < 0) parent.left = e;
    else         parent.right = e;
    fixAfterInsertion(e);//调整
    size++;
    return null;
}

记住每次插入的节点一定是红色：

下面讨论插入后红黑树的变化：

这里只列一下java源代码中的左旋：

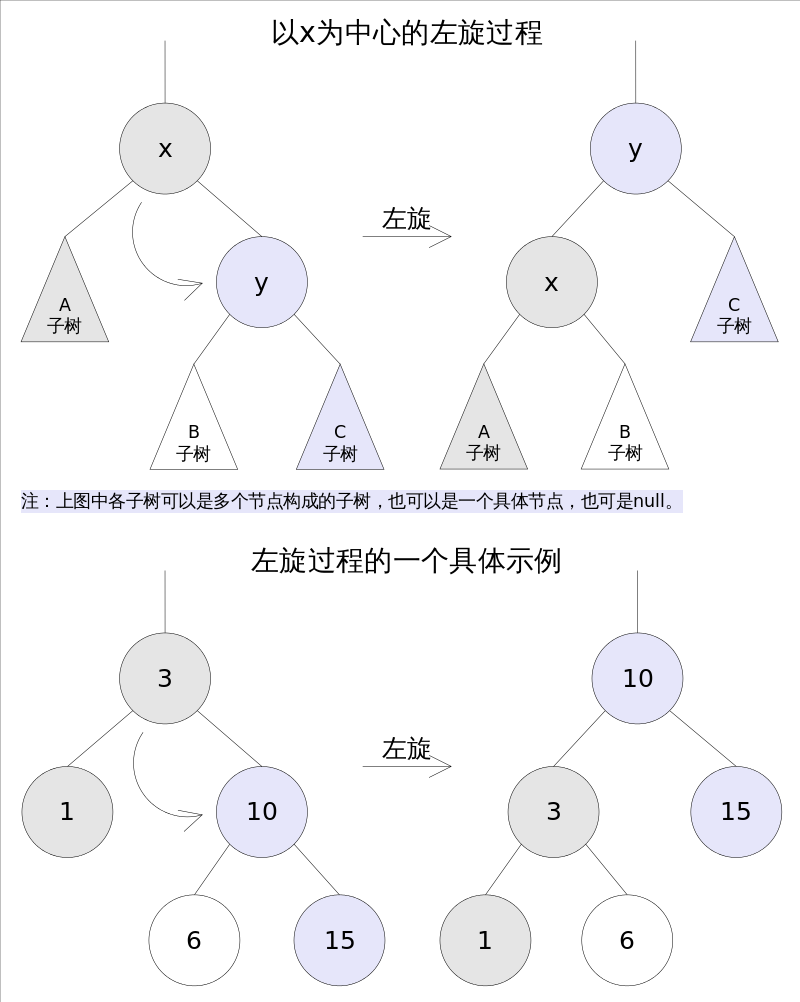
private void rotateLeft(Entry<K,V> p) {
    if (p != null) {
        Entry<K,V> r = p.right;
        p.right = r.left;
        if (r.left != null)
            r.left.parent = p;
        r.parent = p.parent;
        if (p.parent == null)
            root = r;
        else if (p.parent.left == p)
            p.parent.left = r;
        else
            p.parent.right = r;
        r.left = p;
        p.parent = r;
    }
}

主要的变化一般是先变色，再旋转：（红黑树的插入主要是变色，和旋转，正是由于变色的存在，导致旋转的次数很少，这也是红黑树的特点，这里的旋转主要是左旋右旋和AVL树里面的旋转是一样的）

//红黑树调整函数fixAfterInsertion()
private void fixAfterInsertion(Entry<K,V> x) {
    x.color = RED;
    while (x != null && x != root && x.parent.color == RED) {//直接父节点是红色的时候才需要变化，不然直接插入就好了
        if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {  //如果父节点是左节点
            Entry<K,V> y = rightOf(parentOf(parentOf(x)));   //判断父节点的兄弟节点
            if (colorOf(y) == RED) {                       //如果y为null，则视为BLACK //都是红色都要变
                setColor(parentOf(x), BLACK);              // 情况1
                setColor(y, BLACK);                        // 情况1
                setColor(parentOf(parentOf(x)), RED);      // 情况1
                x = parentOf(parentOf(x));                 // 情况1
            } else {
                if (x == rightOf(parentOf(x))) {
                    x = parentOf(x);                       // 情况2
                    rotateLeft(x);                         // 情况2
                }
                setColor(parentOf(x), BLACK);              // 情况3
                setColor(parentOf(parentOf(x)), RED);      // 情况3
                rotateRight(parentOf(parentOf(x)));        // 情况3
            }
        } else {
            Entry<K,V> y = leftOf(parentOf(parentOf(x)));
            if (colorOf(y) == RED) {
                setColor(parentOf(x), BLACK);              // 情况4
                setColor(y, BLACK);                        // 情况4
                setColor(parentOf(parentOf(x)), RED);      // 情况4
                x = parentOf(parentOf(x));                 // 情况4
            } else {
                if (x == leftOf(parentOf(x))) {
                    x = parentOf(x);                       // 情况5
                    rotateRight(x);                        // 情况5
                }
                setColor(parentOf(x), BLACK);              // 情况6
                setColor(parentOf(parentOf(x)), RED);      // 情况6
                rotateLeft(parentOf(parentOf(x)));         // 情况6
            }
        }
    }
    root.color = BLACK;
}

 

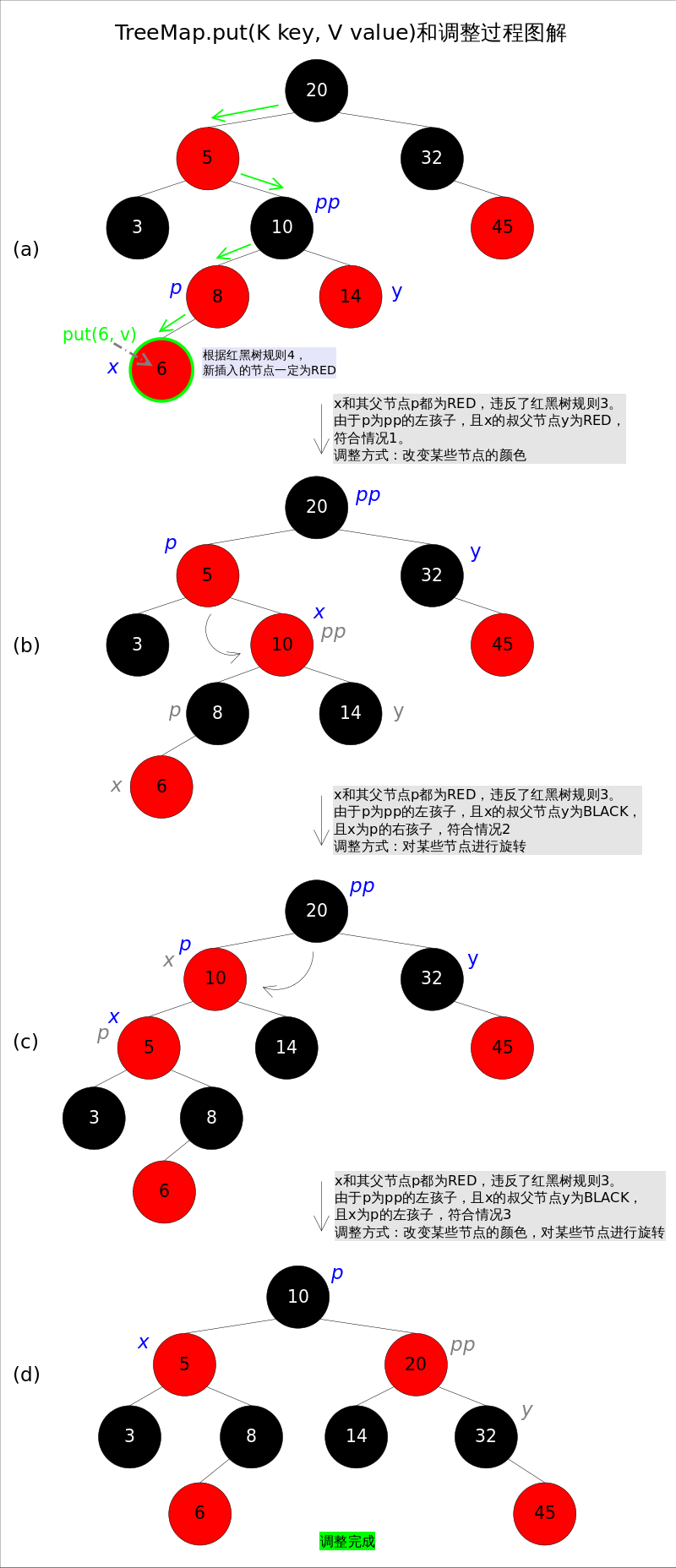
具体的图参考：

https://www.cnblogs.com/CarpenterLee/p/5503882.html

红黑树的删除：

1.被删除节点p的左右节点都为空，直接将p删除。（再删除节点以后需要去判断是否符合红黑树的规则，可能需要需要进行调整，变色左右旋）

2.删除节点p的左右子树都非空，首先寻找p的后继节点（中序遍历），用后继节点代替p，再同样的判断方式去删除这个后继节点，往下一直进行总会遇到情况1的。

在讨论删除：

https://www.cnblogs.com/qingergege/p/7351659.html

 

TreeSet：

TreeSet底层是采用NavigableMap（TreeMap底层也是用这个实现的）实现的一种Set，所以它是有序的，同样也是非线程安全的。

元素要实现Comparable接口等等